Суррогатный алгоритм оптимизации
Последовательный surrogateopt Алгоритм
Последовательный surrogateopt Обзор алгоритма
Суррогатный алгоритм оптимизации чередуется между двумя фазами.
Создайте суррогат — создают
options.MinSurrogatePointsслучайные точки в границах. Выполните (дорогую) целевую функцию в этих точках. Создайте суррогат целевой функции путем интерполяции радиальной основной функции через эти точки.Поиск Минимума — Поиск минимума целевой функции путем выборки нескольких тысяч случайных точек в границах. Оцените оценочную функцию на основе суррогатного значения в этих точках и на расстояниях между ними и точками, где (дорогая) целевая функция была выполнена. Выберите лучшую точку в качестве кандидата, как измерено оценочной функцией. Выполните целевую функцию в лучшей точке кандидата. Эта точка называется adaptive point. Обновите суррогат с помощью этого значения и ищите снова.
Во время фазы Construct Surrogate алгоритм создает точки выборки из квазислучайной последовательности. Построение интерполирующей радиальной основной функции берет, по крайней мере, nvars + 1 точка выборки, где nvars количество переменных задачи. Значение по умолчанию options.MinSurrogatePoints 2*nvars или 20, какой бы ни больше.
Алгоритм останавливает Поиск фазы Minimum, когда все поисковые точки слишком близки (меньше, чем опция MinSampleDistance) к точкам, где целевая функция была ранее выполнена. Смотрите Поиск Минимальных Деталей. Этот переключатель от Поиска фазы Minimum называется surrogate reset.
Определения для суррогатной оптимизации
Суррогатное описание алгоритма оптимизации использует следующие определения.
Текущий — точка, где целевая функция была выполнена последний раз.
Действующий — точка с наименьшим значением целевой функции среди всех оцененных начиная с нового суррогатного сброса.
Лучше всего — точка с наименьшим значением целевой функции среди всех оцененных до сих пор.
Начальная буква — точки, если таковые имеются, что вы передаете решателю в
InitialPointsопция.Случайные точки — Точки в фазе Construct Surrogate, где решатель выполняет целевую функцию. Обычно решатель берет эти точки из квазислучайной последовательности, масштабируемой и переключенной, чтобы остаться в границах. Квазислучайная последовательность похожа на псевдослучайную последовательность, такую как
randвозвращается, но более равномерно расположен с интервалами. См. https://en.wikipedia.org/wiki/Low-discrepancy_sequence. Однако, когда количество переменных выше 500, решатель берет точки из латинской последовательности гиперкуба. См. https://en.wikipedia.org/wiki/Latin_hypercube_sampling.Адаптивные точки — Точки в Поиске фазы Minimum, где решатель выполняет целевую функцию.
Оценочная функция — Видит Определение Оценочной функции.
Оцененные точки — Все точки, в которых известно значение целевой функции. Эти точки включают начальные точки, точки Суррогата Построения и Поиск Минимальных точек, в которых решатель выполняет целевую функцию.
'SamplePoints' . Псевдослучайные точки, где решатель оценивает оценочную функцию во время Поиска фазы Minimum. Эти точки не являются точками, в которых решатель выполняет целевую функцию, за исключением описанного в поисках Минимальных Деталей.
Создайте суррогатные детали
Чтобы создать суррогат, алгоритм выбирает квазислучайные точки в границах. Если вы передаете начальный набор точек в InitialPoints опция, алгоритм использует те точки и новые квазислучайные точки (при необходимости), чтобы достигнуть в общей сложности options.MinSurrogatePoints.
Примечание
Если некоторые верхние границы и нижние границы равны, surrogateopt удаляет те "фиксированные" переменные из проблемы прежде, чем создать суррогат. surrogateopt управляет переменными беспрепятственно. Так, например, если вы передаете начальные точки, передаете полный набор, включая какие-либо фиксированные переменные.
На последующих фазах Construct Surrogate алгоритм использует options.MinSurrogatePoints квазислучайные точки. Алгоритм выполняет целевую функцию в этих точках.
Алгоритм создает суррогат как интерполяцию целевой функции при помощи интерполятора радиальной основной функции (RBF). Интерполяция RBF имеет несколько удобных свойств, которые делают ее подходящей для построения суррогата:
Интерполятор RBF задан с помощью той же формулы в любом количестве размерностей и с любым числом точек.
Интерполятор RBF берет заданные значения в оцененных точках.
Оценка интерполятора RBF занимает время.
Добавление точки к существующей интерполяции занимает относительно мало времени.
Построение интерполятора RBF включает решение N на n линейной системы уравнений, где N является количеством суррогатных точек. Когда Пауэлл [1] показал, эта система имеет уникальное решение для многих RBFs.
surrogateoptиспользует кубический RBF с линейным хвостом. Этот RBF минимизирует меру тряски. Смотрите Гутманна [4].
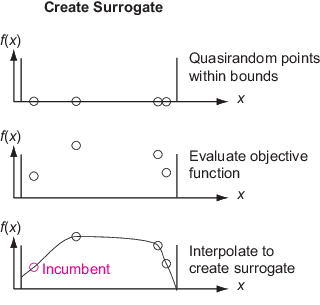
Алгоритм использует только начальные точки и случайные точки в первой фазе Construct Surrogate, и использует только случайные точки в последующих фазах Construct Surrogate. В частности, алгоритм не использует адаптивных точек от Поиска фазы Minimum в этом суррогате.
Ищите минимальные детали
Решатель ищет минимум целевой функции путем выполнения процедуры, которая связана с локальным поиском. Решатель инициализирует scale для поиска со значением 0.2. Шкала похожа на поисковый радиус области или размер mesh в поиске шаблона. Решатель начинает с действующей точки, которая является точкой с наименьшим значением целевой функции начиная с последнего суррогатного сброса. Решатель ищет минимум merit function, который относится и к суррогату и к расстоянию от существующих поисковых точек, чтобы попытаться сбалансировать минимизацию суррогата и поиск пробела. См. Определение Оценочной функции.
Решатель добавляет сотни или тысячи псевдослучайных векторов с масштабированной длиной к действующей точке, чтобы получить sample points. Эти векторы имеют нормальные распределения, переключенные и масштабированные границами в каждой размерности и умноженные на шкалу. При необходимости решатель изменяет точки выборки так, чтобы они остались в границах. Решатель оценивает оценочную функцию при точках выборки, но не в любой точке в options.MinSampleDistance из ранее оцененной точки. Точка с самым низким значением оценочной функции называется адаптивной точкой. Решатель оценивает значение целевой функции в адаптивной точке и обновляет суррогат с этим значением. Если значение целевой функции в адаптивной точке достаточно ниже, чем действующее значение, то решатель считает поиск успешным и устанавливает адаптивную точку как должностное лицо. В противном случае решатель считает поиск неудачным и не изменяет должностное лицо.
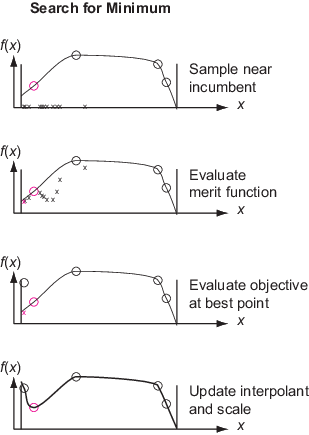
Решатель изменяет шкалу, когда первое из этих условий соблюдают:
Три успешных поисковых запросов происходят начиная с последнего изменения шкалы. В этом случае шкала удвоена до максимальной длины шкалы
0.8времена размер поля заданы границами.max(5,nvar)неудачные поисковые запросы происходят начиная с последнего изменения шкалы, гдеnvarколичество переменных задачи. В этом случае шкала разделена на два, вниз к минимальной длине шкалы1e-5времена размер поля заданы границами.
Таким образом случайный поиск в конечном счете концентрируется около действующей точки, которая имеет маленькое значение целевой функции. Затем решатель геометрически уменьшает шкалу к минимальной длине шкалы.
Решатель не оценивает оценочную функцию при точках в options.MinSampleDistance из оцененной точки (см. Определения для Суррогатной Оптимизации). Переключатели решателя от Поиска фазы Minimum к фазе Construct Surrogate (другими словами, выполняет суррогатный сброс), когда все точки выборки в MinSampleDistance из оцененных точек. Обычно этот сброс происходит после того, как решатель уменьшает шкалу так, чтобы все точки выборки плотно кластеризировались вокруг должностного лица.
Определение оценочной функции
Оценочная функция заслуга f (x) является взвешенной комбинацией двух условий:
Масштабированный суррогат. Задайте min s как минимальное суррогатное значение среди точек выборки, s макс. как максимум и s (x) как суррогатное значение в точке x. Затем масштабированный суррогатный S (x)
s (x) является неотрицательным и является нулем в точках x, которые имеют минимальное суррогатное значение среди точек выборки.
Масштабированное расстояние. Задайте xj, j = 1, …, k, когда k оценил точки. Defiine dij как расстояние от точки выборки i к оцененной точке k. Установите min d = min (dij) и d макс. = макс. (dij), где минимум и максимум взяты по всему i и j. Масштабированное расстояние D (x)
где d (x) является минимальным расстоянием точки x к оцененной точке. D (x) является неотрицательным и является нулем в точках x, которые максимально далеки от оцененных точек. Так, минимизация D (x) приводит алгоритм к точкам, которые далеки от оцененных точек.
Оценочная функция является выпуклой комбинацией масштабированного суррогата и масштабируемого расстояния. Для веса w с 0 <w <1, оценочная функция
Большое значение w дает важность для суррогатных значений, заставляя поиск минимизировать суррогат. Маленькое значение w дает важность для точек, которые далеки от оцененных точек, ведя поиск в новые области. Во время Поиска фазы Minimum, вес циклы w через эти четыре значения, как предложил Режис и Сапожник [2]: 0.3, 0.5, 0.8, и 0.95.
Смешано-целочисленный surrogateopt Алгоритм
Смешано-целочисленный surrogateopt Панорама
Когда некоторые или все переменные - целое число, как задано в intcon аргумент, surrogateopt изменения некоторые аспекты Последовательного surrogateopt Алгоритма. Это описание в основном об изменениях, а не целом алгоритме.
Алгоритм запускается
При необходимости, surrogateopt перемещает заданные границы для intcon точки так, чтобы они были целыми числами. Кроме того, surrogateopt гарантирует, что предоставленная начальная точка является целым числом, выполнимым и выполнимым относительно границ. Алгоритм затем генерирует квазислучайные точки как в алгоритме нецелого числа, округляя целочисленные точки к целочисленным значениям. Алгоритм генерирует суррогат точно как в алгоритме нецелого числа.
Целочисленный поиск минимума
Поиск минимума продолжает с помощью той же оценочной функции и последовательности весов как прежде. Различием является тот surrogateopt использование три различных метода выборки случайных точек, чтобы определить местоположение минимума оценочной функции. surrogateopt выбирает сэмплер в цикле, сопоставленном с весами согласно следующей таблице.
Цикл сэмплера
| Вес | 0.3 | 0.5 | 0.8 | 0.95 |
| Сэмплер | Случайный | Случайный | OrthoMADS | GPS |
Шкала — Каждый сэмплер выборки указывает в масштабированной области вокруг должностного лица. Целочисленные точки имеют шкалу, которая запускается в ½ раза ширине границ и настраивает точно, когда нецелое число указывает, за исключением того, что ширина увеличена до 1, если это когда-либо падало бы ниже 1. Шкала непрерывных точек разрабатывает точно как в алгоритме нецелого числа.
Случайный — сэмплер генерирует целочисленные точки однородно наугад в шкале, сосредоточенной в должностном лице. Сэмплер генерирует непрерывные точки согласно Гауссову со средним нулем от должностного лица. Ширина выборок целочисленных точек умножается на шкалу, как стандартное отклонение непрерывных точек.
OrthoMADS — Сэмплер выбирает систему прямоугольной координаты однородно наугад. Алгоритм затем создает точки выборки вокруг должностного лица, добавляя и вычитая текущие времена шкалы каждый единичный вектор в системе координат. Алгоритм округляет целочисленные точки. Это создает выборки на 2 Н (если некоторые целочисленные точки не округлены должностному лицу), где N является количеством проблемных размерностей. OrthoMADS также использует еще две точки, чем 2 Н зафиксировали направления, один в [+1, +1, …, +1], и другой в [–1, –1, …, –1], для в общей сложности 2N+2 точки. Затем сэмплер неоднократно половины 2 Н + 2 шага, создавая более прекрасный и более прекрасный набор точек вокруг должностного лица, при округлении целочисленных точек. Этот процесс заканчивается, когда или существует достаточно выборок или округления причин никакие новые выборки.
GPS — сэмплер похож на OrthoMADS, кроме вместо того, чтобы выбрать случайный набор направлений, GPS использует невращаемую систему координат.
Поиск по дереву
После выборки сотен или тысяч значений оценочной функции, surrogateopt обычно выбирает минимальную точку и выполняет целевую функцию. Однако при двух обстоятельствах, surrogateopt выполняет другой поиск, названный Поиском по дереву прежде, чем оценить цель:
Были шаги на 2 Н начиная с последнего Поиска по дереву, названного Случаем A.
surrogateoptсобирается выполнить суррогатный сброс, названный Случаем B.
Поиск по дереву продолжает можно следующим образом, похожий на процедуру в intlinprog, как описано в Ветви и Связанный (Optimization Toolbox). Алгоритм делает дерево путем нахождения целочисленного значения и создания новой проблемы, которая имеет привязанный это значение или один выше или один ниже, и решение подпроблемы с этим новым связанный. После решения подпроблемы алгоритм выбирает различное целое число, которое будет ограничено любой выше или ниже одним.
Случай A: Используйте масштабированный радиус выборки в качестве полных границ и запуска максимум для 1 000 шагов поиска.
Случай B: Используйте исходные проблемные границы в качестве полных границ и запуска максимум для 5 000 шагов поиска.
В этом случае решение подпроблемы означает запускать fmincon
'sqp' алгоритм на непрерывных переменных, запускающихся от должностного лица с заданными целочисленными значениями, так ищут локальный минимум оценочной функции.
Поиск по дереву может быть длительным. Так surrogateopt имеет внутреннее ограничение по времени, чтобы избежать чрезмерного времени на этом шаге, ограничивая и количество Случая A и Случай B шаги.
В конце Поиска по дереву алгоритм берет лучше точки, найденной Поиском по дереву и точкой, найденной предыдущим поиском минимума, как измерено оценочной функцией. Алгоритм выполняет целевую функцию в этой точке. Остаток от целочисленного алгоритма является точно тем же самым как непрерывным алгоритмом.
Параллельный surrogateopt Алгоритм
Параллельный surrogateopt алгоритм отличается от последовательного алгоритма можно следующим образом:
Параллельный алгоритм обеспечивает очередь точек, на которых можно выполнить целевую функцию. Эта очередь является на 30% более многочисленной, чем количество параллельных рабочих, окруженных. Очередь является более многочисленной, чем количество рабочих, чтобы свести к минимуму вероятность, что рабочий неактивен, потому что никакой смысл не доступен, чтобы оценить.
Планировщик берет точки из очереди способом FIFO и присваивает их рабочим, когда они становятся неактивными, асинхронно.
Когда переключатели алгоритма между фазами (Поиск Суррогата Минимума и Построения), существующие оцениваемые точки остаются в обслуживании, и любые другие точки в очереди сбрасываются (отброшенный от очереди). Так, обычно, количество случайных точек, которые алгоритм создает для фазы Construct Surrogate, в большей части
options.MinSurrogatePoints + PoolSize, гдеPoolSizeколичество параллельных рабочих. Точно так же после суррогатного сброса, алгоритм все еще имеетPoolSize - 1адаптивные точки, что его рабочие оценивают.
Примечание
В настоящее время найдите что-либо подобное суррогатной оптимизации, не обязательно дает восстанавливаемые результаты, из-за невоспроизводимости параллельной синхронизации, которая может привести к различным путям к выполнению.
Найдите что-либо подобное Смешанному Целому числу surrogateopt Алгоритм
Когда запущено параллельно на смешанной целочисленной задаче, surrogateopt выполняет процедуру Поиска по дереву на хосте, не на параллельных рабочих. Используя последний суррогат, surrogateopt поиски меньшего значения суррогата после каждого рабочего возвращаются с адаптивной точкой.
Если целевая функция не дорога (длительный), то эта процедура Поиска по дереву может быть узким местом на хосте. В отличие от этого, если целевая функция является дорогой, то процедура Поиска по дереву берет небольшую часть полного вычислительного времени и не является узким местом.
Ссылки
[1] Пауэлл, M. J. D. Теория Радиального Приближения Основной функции в 1 990. В Свете, W. A. (редактор), Усовершенствования в Числовом Анализе, Объем 2: Вейвлеты, Алгоритмы Подразделения и Радиальные Основные функции. Нажатие Clarendon, 1992, стр 105–210.
[2] Режис, R. G. и К. А. Шоемэкер. Стохастический Радиальный Метод Основной функции для Глобальной Оптимизации Дорогих Функций. INFORMS J. Вычисляя 19, 2007, стр 497–509.
[3] Ван, Y. и К. А. Шоемэкер. Общая Стохастическая Среда Алгоритма для Минимизации Дорогих Целевых функций Черного квадрата На основе Суррогатных Моделей и Анализа чувствительности. arXiv:1410.6271v1 (2014). Доступный по https://arxiv.org/pdf/1410.6271.
[4] Гутманн, H.-M. Радиальный Метод Основной функции для Глобальной Оптимизации. Журнал Глобальной Оптимизации 19, март 2001, стр 201–227.