Аспектом проекции карты является своя ориентация на странице или экране дисплея. Если север или юг являются прямыми, аспект, как говорят, является экваториальным; для большинства проекций это - нормальный аспект. Когда центральная ось разрабатываемой поверхности ориентирована восток - запад, аспект проекции является поперечным. Проекции, сосредоточенные на Северном полюсе или Южном полюсе, имеют полярный аспект, независимо от того, на что возрос меридиан. Все другие ориентации имеют наклонный аспект. До сих пор примеры и обсуждения отображений карты фокусировались на нормальном аспекте, безусловно обычно используемый. В этом разделе рассматриваются использование поперечных, наклонных, и скошено-наклонных аспектов. Для примера смотрите Управление Аспект Проекции Карты с Вектором Ориентации.
Аспект проекции, в основном, представляет интерес в отображении карт. Однако этот раздел также обсуждает, как идея аспекта проекции как преобразование системы координат может быть применена, чтобы сопоставить переменные в аналитических целях.
Аспект проекции, обсужденный в этом разделе, отличается от осей карты Aspect свойство. Оси карты Aspect свойство управляет ориентацией осей вращения. Например, если карта находится в normal устанавливая с альбомной ориентацией, переключателем к transverse аспект вращает оси на 90 °, приводящие к портретной ориентации. Чтобы отобразить карту в поперечном аспекте, объедините transverse свойство аспекта со скошенным углом на-90 °. Скошенный угол является последним элементом Origin параметр. Например, [0 0 -90] вектор произвел бы поперечную карту.
Карта оси Origin свойство является вектором, описывающим геометрию отображенной проекции. Это свойство Mapping Toolbox™ называется вектором ориентации (предыдущие версии вызвали его вектор источника). Вектор принимает эту форму:
orientvec = [latitude longitude orientation]
Широта и долгота представляют географические координаты центральной точки отображения, от которого вычисляется проекция. Ориентация относится к по часовой стрелке угол от прямого, на который Северный полюс указывает от этой центральной точки. Вектор ориентации по умолчанию [0 0 0]; то есть, проекция сосредоточена на географической точке (0 °, 0 °), и Северный полюс является прямым от этой точки. Такое отображение находится в нормальном аспекте. Изменения только в значении долготы вектора ориентации не изменяют аспект; таким образом нормальным аспектом является тот, сосредоточенный на Экваторе в широте с ориентацией 0 °.
Обе из этих проекций Миллера имеют нормальные аспекты, несмотря на наличие различных векторов ориентации:
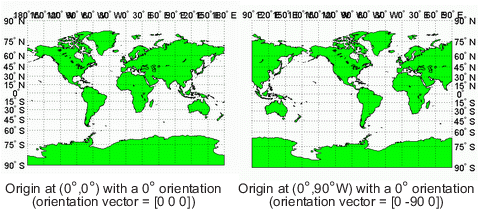
Это целесообразно, если вы думаете о простой, истинной цилиндрической проекции. Это - проекция земного шара на цилиндр, перенесенный это. Для нормальных аспектов этот цилиндр является касательной к земному шару на экватор, и изменение долготы источника просто соответствует вращению сферы о продольной оси цилиндра. Если вы продолжаете перенесенную модель гидроцилиндра, можно изучить другие аспекты также.
После этого описания поперечная проекция может считаться цилиндром, перенесенным во всем мире касательная в полюсах и вдоль меридиана и его диаметрально противоположного меридиана. Наконец, когда такой цилиндр является касательной вдоль любого большого круга кроме меридиана, результатом является наклонная проекция.
Вот схемы четырех цилиндрических ориентаций карты или аспекты:
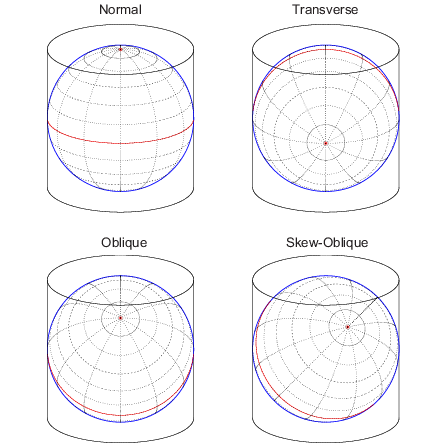
Конечно, немного проекций являются истинными цилиндрическими проекциями, но концепцией перенесенного цилиндра является, тем не менее, удобный способ описать аспект.
Для примера, который использует вектор ориентации, смотрите Управление Аспект Проекции Карты с Вектором Ориентации.
Лучший способ получить понимание аспекта проекции состоит в том, чтобы экспериментировать с векторами ориентации. Следующий пример использует псевдоцилиндрическую проекцию, синусоидальное.
Создайте карту по умолчанию оси в синусоидальной проекции, включите координатную сетку и отобразите набор данных побережья как заполненные многоугольники. Континенты и координатная сетка появляются в нормальном аспекте.
figure; axesm sinusoid framem on; gridm on; tightmap tight load coastlines patchm(coastlat, coastlon,'g') title('Normal aspect: orientation vector = [0 0 0]')

Смотрите вектор ориентации от осей карты. По умолчанию источник установлен в (0°E, 0°N), ориентировал 0 ° от вертикали.
getm(gca,'Origin')ans = 1×3
0 0 0
В нормальном аспекте Северный полюс наверху изображения. Чтобы создать поперечный аспект, предположите раскрывать Северный полюс к центру отображения, которое было первоначально занято точкой (0 °, 0 °). Сделайте это путем установки первого элемента Origin параметр к широте 90°N. Форма системы координат незатронута - это - все еще синусоидальная проекция.
setm(gca,'Origin',[90 0 0]) title('Transverse aspect: orientation vector = [90 0 0]')

Нормальные и поперечные аспекты могут считаться ограничением условий. Что-либо еще - наклонный аспект. Концептуально, если вы пододвигаете Северный полюс обратно на полпути к его исходному положению, то есть, к позиции, первоначально занятой точкой (45°N, 0°E) в нормальном аспекте, результатом является простой наклонный аспект. Можно думать об этом как о получении по запросу нового источника (45°N, 0 °) к центру изображения, место что (0 °, 0 °) занятый в нормальном аспекте.
setm(gca,'Origin',[45 0 0]) title('Oblique aspect: orientation vector = [45 0 0]')

Предыдущие примеры аспекта проекции сохранили ориентацию аспекта на уровне 0 °. Если вы изменяете ориентацию, наклонный аспект становится скошено-наклонной ориентацией. Вообразите предыдущий пример с ориентацией 45 °. Думайте об этом как о получении по запросу нового источника (45°N, 0°E), вниз к центру проекции и затем вращения проекции, пока Северный полюс не найдется под углом 45 ° по часовой стрелке от прямого относительно нового источника. Как в предыдущем примере, местоположение (45°N, 0°E) все еще занимает центр карты.
setm(gca,'Origin',[45 0 45]) title('Skew-Oblique aspect: orientation vector = [45 0 45]')

Основная проекция может считаться стандартной системой координат, и нормальный аспект соответствует ей. Функции проекции обеспечены в любом аспекте относительно основной проекции. Когда предыдущие рисунки показывают, схема (система координат) не изменяется. Ненаправленные характеристики проекции также не изменяются. Например, синусоидальная проекция является равной областью, неважно, что ее аспект. Направленные характеристики должны быть рассмотрены тщательно, как бы то ни было. В нормальном аспекте синусоидальной проекции шкала верна вдоль каждой параллели и центрального меридиана. Дело обстоит не так для скошено-наклонного аспекта; однако, шкала верна вдоль путей преобразованных параллелей и меридиана.
Любая проекция может быть просмотрена в альтернативных аспектах, и это может часто быть довольно полезно. Например, поперечный аспект Меркаторской проекции широко используется в картографии, специально для отображения областей с преимущественно между севером и югом степенью. Одним кандидатом на такую обработку может быть Чили. Наклонные Меркаторские проекции могут использоваться, чтобы сопоставить длинные области, которые не запускают ни севера и юга, ни востока и запада, такого как Новая Зеландия.