Оптимизация нелинейных функций

Минимизация функций одной переменной

Учитывая математическую функцию одной переменной, можно использовать fminbnd функционируйте, чтобы найти локальный минимизатор функции в данном интервале. Например, рассмотрите humps.m функция, которой предоставляют MATLAB®. Следующий рисунок показывает график humps.

x = -1:.01:2;
y = humps(x);
plot(x,y)
xlabel('x')
ylabel('humps(x)')
grid on

Найти минимум humps функция в области значений (0.3,1)Использование

x = fminbnd(@humps,0.3,1)

x = 0.6370

Вы видите детали процесса решения при помощи optimset создать опции с Display набор опции к 'iter'. Передайте получившиеся опции fminbnd.

options = optimset('Display','iter');
x = fminbnd(@humps,0.3,1,options)

 
 Func-count     x          f(x)         Procedure
    1       0.567376      12.9098        initial
    2       0.732624      13.7746        golden
    3       0.465248      25.1714        golden
    4       0.644416      11.2693        parabolic
    5         0.6413      11.2583        parabolic
    6       0.637618      11.2529        parabolic
    7       0.636985      11.2528        parabolic
    8       0.637019      11.2528        parabolic
    9       0.637052      11.2528        parabolic
 
Optimization terminated:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04

x = 0.6370

Итеративное отображение показывает текущее значение x и значение функции в f(x) каждый раз функциональная оценка происходит. Для fminbnd, одна функциональная оценка соответствует одной итерации алгоритма. Последний столбец показывает процедуре fminbnd использование в каждой итерации, золотой раздел ищет или параболическая интерполяция. Для получения дополнительной информации смотрите Итеративное Отображение.

Минимизация функций нескольких переменных

fminsearch функция похожа на fminbnd за исключением того, что это обрабатывает функции многих переменных. Задайте стартовый вектор x0, а не стартовый интервал. fminsearch попытки возвратить вектор x, который является локальным минимизатором математической функции около этого стартового вектора.

Попробовать fminsearch, создайте функциональный three_var из трех переменных, xY, и z.

function b = three_var(v)
x = v(1);
y = v(2);
z = v(3);
b = x.^2 + 2.5*sin(y) - z^2*x^2*y^2;

Теперь найдите минимум для этой функции с помощью x = -0.6, y = -1.2, и z = 0.135 как начальные значения.

v = [-0.6,-1.2,0.135];
a = fminsearch(@three_var,v)

a =
    0.0000   -1.5708    0.1803

Максимизация функций

fminbnd и fminsearch решатели пытаются минимизировать целевую функцию. Если у вас есть проблема максимизации, то есть, проблема формы

$\max_{x} f (x),$

затем задайте g (x) = –f (x) и минимизируйте g.

Например, чтобы найти максимум tan (cos (x)) около x = 5, оцените:

[x fval] = fminbnd(@(x)-tan(cos(x)),3,8)

x =
    6.2832

fval =
   -1.5574

Максимум 1.5574 (отрицание fval, о котором сообщают,), и происходит в x = 6.2832. Этот ответ правилен с тех пор к пяти цифрам, максимум коричнев (1) = 1.5574, который происходит в x = 2π = 6.2832.

`fminsearch` Алгоритм

fminsearch использует алгоритм симплекса Nelder-меда как описано в Lagarias и др. [1]. Этот алгоритм использует симплекс n + 1 точка для n - размерные векторы x. Алгоритм сначала делает симплекс вокруг исходного предположения x ₀ путем добавления 5% каждого x компонента ₀ (i) к x ₀. Алгоритм использует эти векторы n в качестве элементов симплекса в дополнение к x ₀. (Алгоритм использует 0.00025 в качестве i компонента если x ₀ (i) = 0.) Затем алгоритм неоднократно изменяет симплекс согласно следующей процедуре.

Примечание

Ключевые слова для fminsearch итеративное отображение появляется полужирным после описания шага.

Позволенный x (i) обозначают список точек в текущем симплексе, i = 1..., n +1.
Закажите точки в симплексе от самого низкого значения функции f (x (1)) к самому высокому f (x (n +1)). На каждом шаге в итерации алгоритм отбрасывает текущую худшую точку x (n +1) и принимает другую точку в симплекс. [Или, в случае шага 7 ниже, это изменяет все точки n со значениями, больше, чем f (x (1))].
Сгенерируйте точку reflected
r = 2m – x (n +1),
где
m = Σx (i)/n, i = 1... n,
и вычислите f (r).
Если f (x (1)) ≤ f (r) <f (x (n)), примите r и отключите эту итерацию. Отразиться
Если f (r) <f (x (1)), вычислите, расширение указывают s
s = m + 2 (m – x (n +1)),
и вычислите f (s).
1. Если f (s) <f (r), примите s и отключите итерацию. Расширение
2. В противном случае примите r и отключите итерацию. Отразиться
Если f (r) ≥ f (x (n)), выполните contraction между m и лучше x (n +1) и r:
1. Если f (r) <f (x (n +1)) (то есть, r лучше, чем x (n +1)), вычислить
  c = m + (r – m)/2
  и вычислите f (c). Если f (c) < f (r), примите c и отключите итерацию. Контракт снаружи В противном случае, продолжите Шаг 7 (Уменьшение).
2. Если f (r) ≥ f (x (n +1)), вычислить
  cc = m + (x (n +1) – m)/2
  и вычислите f (cc). Если f (cc) < f (x (n +1)), примите cc и отключите итерацию. Контракт внутри В противном случае, продолжите Шаг 7 (Уменьшение).
Вычислите точки n
v (i) = x (1) + (x (i) – x (1))/2
и вычислите f (v (i)), i = 2..., n +1. Симплексом в следующей итерации является x (1), v (2)..., v (n +1). Уменьшение

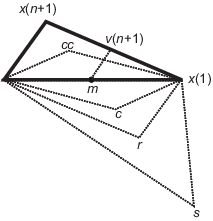
Следующий рисунок показывает точки что fminsearch может вычислить в процедуре, наряду с каждым возможным новым симплексом. Исходный симплекс имеет полужирную схему. Итерации продолжают, пока они не соответствуют останавливающемуся критерию.

Ссылка

[1] Lagarias, J. C. Дж. А. Ридс, М. Х. Райт и П. Э. Райт. “Свойства сходимости Симплекс-метода Nelder-меда в Низких Размерностях”. SIAM Journal Оптимизации, Издания 9, Номера 1, 1998, стр 112–147.

Документация