Документация

lsqnonlin с Моделью Simulink

Предположим, что вы хотите оптимизировать параметры управления в модели optsim.mdl Simulink^®. (Эта модель может быть найдена в optim/optimdemos папка. Обратите внимание на то, что Simulink должен быть установлен в вашей системе, чтобы загрузить эту модель.) Модель включает нелинейный обрабатывающий завод, смоделированный как Диаграмму Simulink.

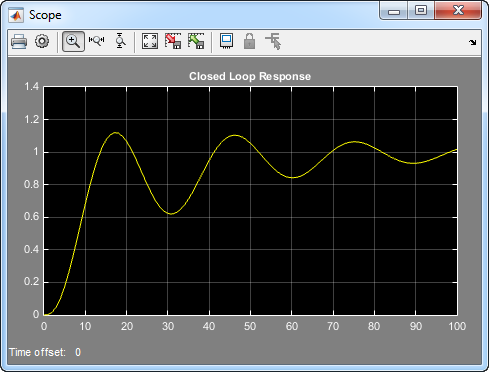
Объект под - ослабленная модель третьего порядка с пределами привода. Пределы привода являются пределом насыщения и пределом скорости нарастания. Предел насыщения привода отключает входные значения, больше, чем 2 модуля или меньше чем-2 модуля. Предел скорости нарастания привода является 0,8 модулями/секунда. Ответ с обратной связью системы к входу шага показывают в Ответе С обратной связью. Вы видите, этот ответ путем открытия модели (введите optsim в командной строке или нажатии кнопки имя модели), и Run выбора в меню Simulation. Графики отклика к осциллографу.

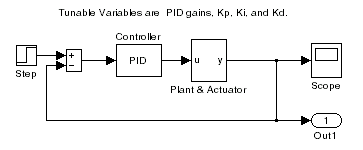
Проблема состоит в том, чтобы спроектировать цикл управления с обратной связью, который отслеживает модульный вход шага к системе. Объект с обратной связью вводится в терминах блоков, куда объект и привод были помещены в иерархический блок Subsystem. Блок Scope отображает выходные траектории во время процесса проектирования.

Один способ решить эту задачу состоит в том, чтобы минимизировать ошибку между выходом и входным сигналом. Переменные являются параметрами контроллера Пропорциональной интегральной производной (PID). Если бы только необходимо минимизировать ошибку когда-то модуль, это была бы одна целевая функция. Но цель состоит в том, чтобы минимизировать ошибку, навсегда продвигается от 0 до 100, таким образом производя многоцелевую функцию (одна функция для каждого временного шага).

Стандартный lsqnonlin используется, чтобы выполнить подгонку наименьших квадратов на отслеживании выхода. Отслеживание выполняется через функциональный tracklsq, который возвращает сигнал ошибки yout, выход вычисляется путем вызова sim, минус входной сигнал 1. Код для tracklsq содержится в файле runtracklsq.m, показанный ниже.

Функциональный runtracklsq настраивает все необходимые значения и затем вызывает lsqnonlin с целевой функцией tracklsq, который вкладывается в runtracklsq. Переменная options переданный lsqnonlin задает характеристики отображения и критерии. В этом случае вы просите выход, используете 'levenberg-marquardt' алгоритм, и дает допуски завершения к ступенчатой и целевой функции на порядке 0.001.

Запускать симуляцию в модели optsim, переменные Kp, Ki, Kd, a1, и a2 (a1 и a2 переменные в блоке Plant), должен все быть задан. Kp, Ki, и Kd переменные должны быть оптимизированы. Функциональный tracklsq вкладывается в runtracklsq так, чтобы переменные a1 и a2 совместно используются двумя функциями. Переменные a1 и a2 инициализируются в runtracklsq.

Целевая функция tracklsq запускает симуляцию. Симуляция может быть запущена или в базовом рабочем пространстве или в текущей рабочей области, то есть, рабочей области функции, вызвав sim, который в этом случае является рабочей областью tracklsq. В этом примере, SrcWorkspace опция установлена в 'Current' сказать sim запускать симуляцию в текущей рабочей области. Симуляция выполняется к 100 секунды.

Когда симуляция завершается, myobj объект создается в текущей рабочей области (то есть, рабочая область tracklsq). Блок Outport в модели блок-схемы помещает yout поле объекта в текущую рабочую область в конце симуляции.

Следующее является кодом для runtracklsq:

function [Kp,Ki,Kd] = runtracklsq
% RUNTRACKLSQ demonstrates using LSQNONLIN with Simulink.

optsim                       % Load the model
pid0 = [0.63 0.0504 1.9688]; % Set initial values
a1 = 3; a2 = 43;             % Initialize model plant variables
options = optimoptions(@lsqnonlin,'Algorithm','levenberg-marquardt',...
   'Display','off','StepTolerance',0.001,'OptimalityTolerance',0.001);
pid = lsqnonlin(@tracklsq, pid0, [], [], options);
Kp = pid(1); Ki = pid(2); Kd = pid(3); 

    function F = tracklsq(pid)
      % Track the output of optsim to a signal of 1
        
      % Variables a1 and a2 are needed by the model optsim.
      % They are shared with RUNTRACKLSQ so do not need to be
      % redefined here.
      Kp = pid(1);
      Ki = pid(2);
      Kd = pid(3);

      % Set sim options and compute function value
      myobj = sim('optsim','SrcWorkspace','Current', ...
          'StopTime','100');
      F = myobj.get('yout') - 1;
    end
end

Скопируйте код для runtracklsq в файл с именем runtracklsq.m, помещенный в папку на вашем пути MATLAB^®.

Когда вы запускаете runtracklsq, оптимизация дает решение для пропорционального, интеграла и производной (Kp, Ki, Kd) усиления контроллера:

[Kp, Ki, Kd] = runtracklsq

Kp =
    3.1330

Ki =
    0.1465

Kd =
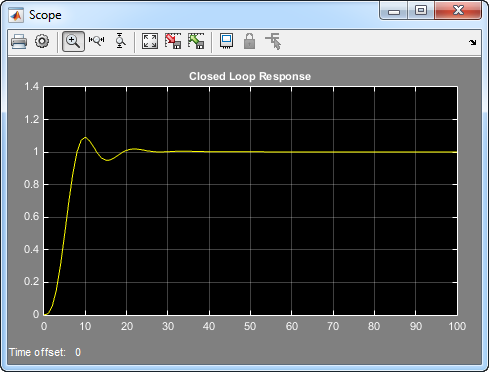
   14.3918

Вот получившийся переходной процесс с обратной связью.