Exponenta Banner

Luenberger Observer

Дискретное время наблюдатель Luenberger

расширьте все на странице
  • Библиотека:

  • Simscape / Электрический / Управление / Наблюдатели

Описание

Блок Luenberger Observer реализует дискретное время наблюдатель Luenberger. Используйте этот блок, чтобы оценить состояния заметного системного использования:

  • Дискретные вводы и выводы системы.

  • Дискретное представление пространства состояний системы.

Наблюдатель Luenberger также иногда упоминается как наблюдатель состояния или просто наблюдатель.

Можно управлять мультивходом, мультивывести системы путем передачи вектора состояния вывода этого блока с блоком State Feedback Controller.

Определение уравнений

Блок реализует дискретное время Наблюдатель Luenberger, использующий обратный Метод Эйлера из-за его простоты и устойчивости.

Средство оценки дано этим разностным уравнением:

x^(k+1) =Adx^(k) +Bdu(k) + Ld(y(k) −y^(k)),

где:

  • x^(k) k th оцененный вектор состояния.

  • y^(k) k th оцененный выходной вектор.

  • u(k) является k th входной вектор.

  • y(k) является k th измеренный выходной вектор.

  • Ad является дискретизированной матрицей состояния.

  • Bd является дискретизированной входной матрицей.

  • Ld является дискретизированной матрицей усиления наблюдателя.

Движущие силы ошибки оценки описаны:

e(k+1)=(Ad−LdCd)e(k),

где:

  • e(k) является k th вектор ошибок.

  • Cd является выходной матрицей.

Ошибка оценки сходится, чтобы обнулить, когда Ad-LdCd имеет свои собственные значения в модульном кругу. Поэтому значение Ld должно быть таково, что эта цель достигается. Блок вычисляет усиление наблюдателя путем решения

LdT=GX−1,

где G является произвольной матрицей, и X получен путем решения уравнения Сильвестра:

AdTX−XΛ=CdTG.

Здесь, Λ является матрицей с желаемыми собственными значениями, которые не являются тем же самым как собственными значениями Ad. Эта схема показывает базовую структуру дискретного времени Наблюдатель Luenberger.

Предположения

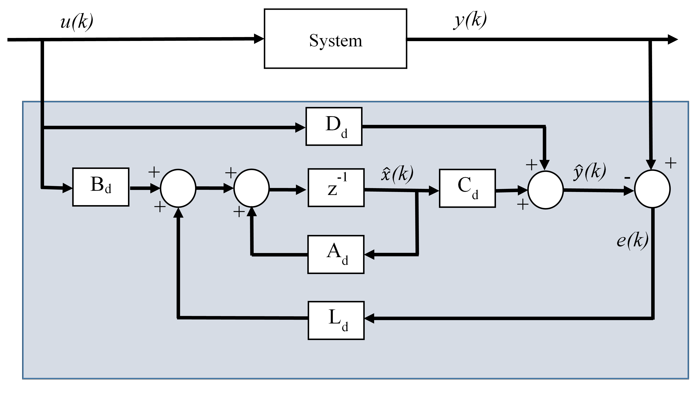
Система заметна, который верен, если состояние системы может быть определено из ввода и вывода в конечный промежуток времени. Математически, это означает, что системная матрица наблюдаемости имеет полный ранг.

Ограничения

Желаемые собственные значения не являются тем же самым как собственными значениями модели разомкнутого цикла.

Порты

Входной параметр

развернуть все

Входной сигнал к системе, чье состояние мы хотим оценить, заданный как вектор.

Типы данных: single | double

Измеренный выход системы, чье состояние мы хотим оценить, заданный как вектор.

Типы данных: single | double

Вывод

развернуть все

Оценка состояния системы, заданной как вектор.

Типы данных: single | double

Параметры

развернуть все

Выберите стратегию параметризации матриц пространства состояний и желаемых полюсов для наблюдателя. Реализация блока дискретна независимо от этой параметризации.

Матрица состояния модели в пространстве состояний дискретного времени. Матрица A должна быть квадратной с количеством строк и столбцов, равных порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Discrete-time.

Введите матрицу модели в пространстве состояний дискретного времени. Матрица B должна иметь количество строк, равных порядку системы и количеству столбцов, равных количеству системных входных параметров.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Discrete-time.

Выходная матрица модели в пространстве состояний дискретного времени. Матрица C должна иметь количество строк, равных количество выходных параметров системы и количество столбцов, равных порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Discrete-time.

Проходная матрица модели в пространстве состояний дискретного времени. Матрица D должна иметь количество строк, равных количеству системы выходные параметры и количество столбцов, равных количеству системных входных параметров.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Discrete-time.

Матрица состояния модели в пространстве состояний непрерывного времени. Матрица A должна быть квадратной с количеством строк и столбцов, равных порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Continuous-time.

Введите матрицу модели в пространстве состояний непрерывного времени. Матрица B должна иметь количество строк, равных порядку системы и количеству столбцов, равных количеству системных входных параметров.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Continuous-time.

Выходная матрица модели в пространстве состояний непрерывного времени. Матрица C должна иметь количество строк, равных количество выходных параметров системы и количество столбцов, равных порядку системы.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Continuous-time.

Проходная матрица модели в пространстве состояний непрерывного времени. Матрица D должна иметь количество строк, равных количеству системы выходные параметры и количество столбцов, равных количеству системных входных параметров.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Continuous-time.

Выберите стратегию параметризации усиления наблюдателя.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Discrete-time.

Задайте усиление наблюдателя, которое помещает все собственные значения матричного Ad-LdCd в модульном кругу. Матрица усиления должна иметь количество строк, равных количеству системных входных параметров и количеству столбцов, равных порядку системы.

Зависимости

Чтобы включить этот параметр, установите:

  • State-space parameterization к Discrete-time.

  • Observer design к Observer gain.

Задайте местоположение собственных значений:

  • Иметь отрицательную действительную часть, если State-space parameterization установлен в Continuous-time. В этом случае собственные значения системы непрерывного времени аппроксимированы к дискретным единицам на основе Discretization sample time.

  • Лечь в модульном кругу, если State-space parameterization установлен в Discrete-time.

Усиление The Observer затем вычисляется на основе этих собственных значений. Размер вектора должен совпасть с системным порядком.

Выберите начальное условие каждого состояния.

Значение раньше дискретизировало матрицы пространства состояний и также аппроксимировало собственные значения дискретного времени.

Зависимости

Чтобы включить этот параметр, установите State-space parameterization на Continuous-time.

Значение раньше симулировало динамику модели. Выберите то же значение в качестве Discretization sample time, если блок не помещается в инициированной подсистеме, в этом случае необходимо установить его на-1.

Примеры модели

DC Motor Control (State-Feedback and Observer)

Управление двигателем постоянного тока (Обратная связь состояния и наблюдатель)

Структура регулировки скорости обратной связи состояния для двигателя постоянного тока. Управляемый Прерыватель PWM с четырьмя квадрантами используется, чтобы питать двигатель постоянного тока. Подсистема Управления включает цикл управления с обратной связью состояния и генерацию PWM. Вектор состояния включает скорость ротора, которая измеряется, и текущий двигатель постоянного тока, который оценивается с помощью наблюдателя. И наблюдатель и диспетчер обратной связи состояния синтезируются размещением полюса с помощью модели в пространстве состояний системы. Общее время симуляции (t) составляет 4 секунды. В t = 1,5 секунды, увеличения крутящего момента загрузки. В t = 2,5 секунды, ссылочная скорость изменяется с 1 000 об/мин до 2 000 об/мин.

Открытая модель
PMSM Position Control

Управление положением PMSM

Управляйте положением ротора в базирующемся электрическом диске PMSM. Идеальный источник крутящего момента обеспечивает загрузку. Подсистема Управления использует структуру каскадного регулирования с двумя циклами управления, внешним циклом для положения и регулировки скорости и внутреннего цикла для текущего управления. Оптимальная обратная связь состояния линейный квадратичный регулятор управляет положением и скоростью. Наблюдатель Luenberger оценивает загрузку. Внутренний контур управления током реализован с помощью ПИ-контроллеров. PMSM питается управляемым трехфазным инвертором. Симуляция использует ссылки шага. Подсистема Осциллографов содержит осциллографы, которые позволяют вам видеть результаты симуляции.

Открытая модель
Synchronous Machine State-Space Control

Синхронное управление пространства состояний машины

Управляйте токами в основанном на синхронной машине (SM) диске тяги с помощью управления пространства состояний. Высоковольтная батарея питает SM через управляемый трехфазный конвертер для обмоток статора и через управляемый 2D квадрантный прерыватель для обмотки ротора. Идеальный источник скорости вращения обеспечивает загрузку. SM действует ниже основной скорости. В каждый демонстрационный момент запрос крутящего момента преобразован в соответствующие текущие ссылки с помощью нулевого подхода управления d-оси. Контроллер обратной связи состояния управляет токами в системе координат ротора. Наблюдатель Luenberger получает зависимые скоростью условия feedforward перед управлением. Симуляция использует несколько шагов крутящего момента и в режимах двигателя и в генератора. Планирование задач реализовано как конечный автомат Stateflow®. Подсистема Осциллографов содержит осциллографы, которые позволяют вам видеть результаты симуляции.

Открытая модель

Ссылки

[1] Luenberger, D. G. "Введение в Наблюдателей". Транзакции IEEE на Автоматическом управлении. Издание 16, Номер 6, 1971, стр 596-602.

[2] Alessandri, A. и П. Колетта. "Проект наблюдателей Luenberger для класса гибридных линейных систем". На Международном семинаре на Гибридных системах: Расчет и Управление, Берлин, март 2001.

[3] Varga, A. "Устойчивое присвоение полюса через Сильвестра основанная на уравнении параметризация обратной связи состояния". В Автоматизированном Проекте Системы управления, стр 13-18., Анкоридж, Аляска, 2000.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Блоки

Введенный в R2017b

Документация Simscape Electrical
Поддержка