Анализируйте отношение между параметрами и конструктивными требованиями

Чтобы анализировать, как параметры и состояния (коллективно называемый parameters) модели Simulink^® влияют на конструктивные требования на сигналах модели, вы сначала генерируете выборки параметров. Вы затем задаете функцию стоимости путем создания конструктивных требований на сигналах модели и оцениваете функцию стоимости для каждой выборки. Наконец, вы анализируете отношение между изменениями параметра и значениями функции стоимости. Можно выполнить этот анализ следующими способами:

Визуальный анализ

Просмотрите график оценок функции стоимости против выборок параметра, чтобы идентифицировать тренды. Этот метод является неофициальным и обеспечивает визуальную интуицию о том, как различные параметры влияют на функцию стоимости.

В инструменте Sensitivity Analysis, после того, как оценка завершена, график рассеивания результата оценки сгенерирован в инструменте. График отображает оцененное значение функции стоимости как функцию каждого параметра в наборе параметра. Последний подграфик столбца отображает вероятностное распределение оцененных значений функции стоимости. Можно добавить наилучшую эмпирическую кривую в поля точек подграфики путем щелчка правой кнопкой по графику и выбора Overlay linear fit в контекстном меню. В этом графике наилучшая эмпирическая кривая указывает что Gain параметр имеет большое влияние на требование.

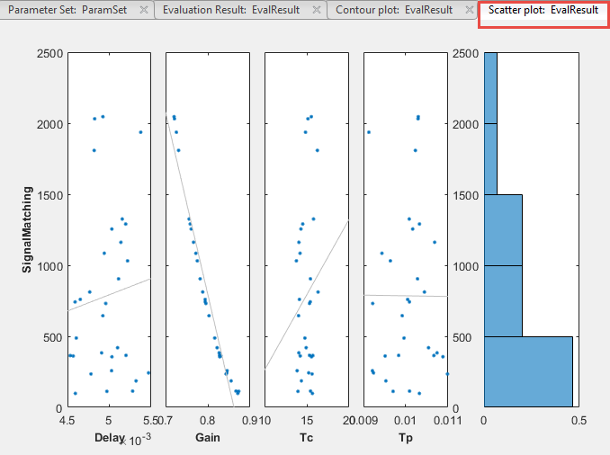
Можно также построить контурный график оцененных результатов. Чтобы узнать больше об этих графиках, смотрите, Взаимодействуют с Графиками в Sensitivity Analysis Tool. Для примера смотрите, Идентифицируют Основные параметры для Оценки (графический интерфейс пользователя).

В командной строке можно использовать инструменты, такие как:

sdo.scatterPlot — График поля точек выборок параметра против оценки функции стоимости
surfmeshконтур — 3-D график выборок двух параметров против оценки функции стоимости

Для примера смотрите, Идентифицируют Основные параметры для Оценки (Код).

Статистический анализ

В дополнение к визуальному анализу эффекта параметров на функции стоимости можно также вычислить статистику, чтобы определить количество отношения.

Получите итоговую статистику об отношении между оценками функции стоимости и выборками параметров. Доступные методы анализа включают:

Метод	Описание
Корреляция	Используйте, чтобы анализировать, как коррелируются параметр модели и функция стоимости выход.
Частичная Корреляция (требует программного обеспечения Statistics and Machine Learning Toolbox™),	Используйте, чтобы анализировать, как параметр модели и функция стоимости коррелируются, удаляя эффекты остающихся параметров.
Стандартизированная регрессия	Используйте, когда вы ожидаете, что параметры модели линейно влияют на функцию стоимости.

Для каждого из этих методов вы задаете, какие данные использовать в анализе путем выбора из следующего анализа вводит:

Линейный анализ, также называемый анализом Pearson — необработанные данные Использования для анализа. Используйте линейный анализ, когда вы ожидаете линейное отношение между параметрами и функцией стоимости, и когда остаточные значения о наилучшей эмпирической кривой, как будут ожидать, будут нормально распределены. Линейный анализ также рекомендуется, когда количество выборок, и таким образом, количество остаточных точек является большим.
Оцениваемый анализ, также называемый анализом Spearman и ranked transformation — ранги Использования данных для анализа. Используйте оцениваемый анализ, когда вы ожидаете нелинейное монотонное отношение между параметрами и функцией стоимости и когда остаточные значения о наилучшей эмпирической кривой не будут нормально распределены. Оцениваемый анализ также рекомендуется, когда количество выборок, и таким образом, количество остаточных точек мало.
Линейный анализ сохраняет информацию об интервалах между значениями данных, тогда как оцениваемый анализ не делает. Предположим, что у вас был следующий набор данных:
_x1 _x2 y
9 20 340
5 60 106
2.3 50.4 870.5
Здесь _x1 и _x2 являются параметрами модели, и y является функцией стоимости. Каждая строка представляет выборку и связанную оценку функции стоимости.
Данные оцениваются на основе для каждого столбца. Например, когда вы оцениваете данные в столбце 1 (_x1), который содержит записи 9, 5, и 2.3, оцениваемые данные равны 3, 2, и 1. Оцениваемый набор данных для выборок _x1, _x2 и y следующие:
_x1 _x2 y
3 1 2
2 3 1
1 2 3
Оцениваемый набор данных может использоваться в корреляции, частичной корреляции или стандартизированном регрессионном анализе.
Кендалл — tau коэффициент порядковой корреляции Кендалла вычисляется.
Применимый, когда методом анализа является Корреляция. Программное обеспечение Requires Statistics and Machine Learning Toolbox.

_x1	_x2	y
9	20	340
5	60	106
2.3	50.4	870.5

_x1	_x2	y
3	1	2
2	3	1
1	2	3

Метод корреляции

Вычисляет коэффициенты корреляции, R. Используйте этот метод, чтобы анализировать, как коррелируются параметр модели и функция стоимости выходные параметры.

R вычисляется можно следующим образом:

$\begin{array}{l} R (i, j) & = \frac{C (i, j)}{\sqrt{C (i, i) C (j, j)}} \\ C & = c o v (x, y) \\ = E [(x - μ_{x}) (y - μ_{y})] \\ μ_{x} & = E [x] \\ μ_{y} & = E [y] \end{array}$

x содержит выборки Ns параметров модели Np. y содержит строки Ns, каждая строка соответствует оценке функции стоимости для выборки в x.

Значения R находятся в [-1 1] область значений. (i, j) запись R указывает на корреляцию между x (i) и y (j).

R(i,j) > 0 — Переменные имеют положительную корреляцию. Переменные увеличиваются вместе.
R(i,j) = 0 — Переменные не имеют никакой корреляции.
R(i,j) < 0 — Переменные имеют отрицательную корреляцию. Когда одна переменная увеличивается, другие уменьшения.

Частичный метод корреляции

Вычисляет частичные коэффициенты корреляции, R. Этот метод требует программного обеспечения Statistics and Machine Learning Toolbox. Используйте этот метод, чтобы анализировать, как параметр модели и функция стоимости коррелируются, настраивая, чтобы удалить эффект других параметров.

R вычисляется с помощью partialcorri из программного обеспечения Statistics and Machine Learning Toolbox.

Стандартизированный метод регрессии

Вычисляет стандартизированные коэффициенты регрессии, R. Используйте этот метод, когда вы ожидаете, что параметры модели линейно влияют на функцию стоимости.

R вычисляется можно следующим образом:

$R = b_{x} \frac{σ_{x}}{σ_{y}}$

Рассмотрите одну выборку (_x1..., x Np) и соответствующий один выход, y. _bx является вектором коэффициента регрессии, вычисленным с помощью наименьших квадратов, принимающих линейную модель $\hat{y} = b_{0} + \sum_{i = 1}^{N p} {\hat{b}}_{x_{i}} x_{i}$ . R стандартизирует каждый элемент _bx путем умножения его с отношением стандартного отклонения соответствующей выборки x (_σx) к стандартному отклонению y (_σy).

Выполните статистический анализ

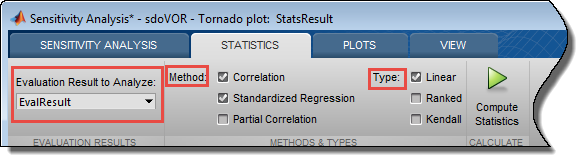
В инструменте Sensitivity Analysis, после того, как вы оценили конструктивные требования, задают методы анализа и типы во вкладке Statistics инструмента.

Выберите результаты оценки, которые вы хотите анализировать в списке Evaluation Results to Analyze. После этого вы задаете методы анализа и типы, и нажимаете Compute Statistics. Можно вычислить все применимые комбинации методов анализа и типов.

Результаты анализа возвращены в StatsResult переменная, в области Results инструмента. В этом случае, StatsResult переменная включает линейное (Пирсон) коэффициенты корреляции и линейные стандартизированные коэффициенты регрессии, вычисленные между функцией стоимости и каждым параметром. Чтобы видеть коэффициенты, щелкните правой кнопкой по StatsResult, и выберите Open в контекстном меню.

График торнадо сгенерирован, который отображает результаты анализа в порядке влияния параметров на функции стоимости. Параметр, что большинство влияний функция стоимости отображено на верхней части. Как был замечен в графике рассеивания результатов, в этом графике торнадо Gain параметр имеет большую часть влияния на функцию стоимости конструктивных требований.

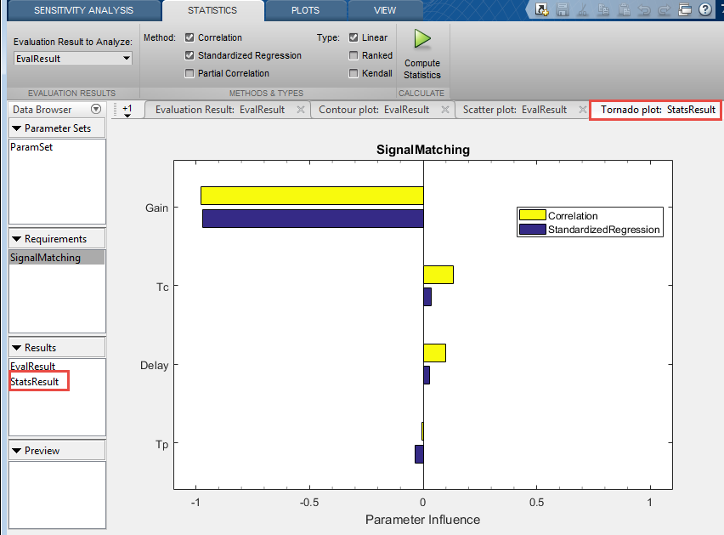
Чтобы узнать больше о графиках торнадо, смотрите, Взаимодействуют с Графиками в Sensitivity Analysis Tool. Для примера смотрите, Идентифицируют Основные параметры для Оценки (графический интерфейс пользователя).

В командной строке задайте методы анализа и типы с помощью sdo.analyze. Эта функция выполняет анализ линейной корреляции по умолчанию. Чтобы задать другие методы анализа, используйте sdo.AnalyzeOptions. Для примера смотрите, Идентифицируют Основные параметры для Оценки (Код).

Документация