Гауссовы модели регрессии процесса

Модели гауссовой регрессии процесса (GPR) являются непараметрическими основанными на ядре вероятностными моделями. Можно обучить модель GPR с помощью fitrgp функция.

Рассмотрите набор обучающих данных ${(x_{i}, y_{i}); i = 1, 2, ..., n}$ , где $x_{i} \in ℝ^{d}$ и $y_{i} \in ℝ$ , чертивший от неизвестного распределения. Модель GPR обращается к вопросу предсказания значения переменной отклика $y_{n e w}$ , учитывая новый входной вектор $x_{n e w}$ , и обучающие данные. Модель линейной регрессии имеет форму

$y = x^{T} β + ε,$

где $ε \sim N (0, σ^{} 2)$ . Ошибочное отклонение σ ² и коэффициенты β оценивается из данных. Модель GPR объясняет ответ путем представления скрытых переменных, $f (x_{i}), i = 1, 2, ..., n$ , от Гауссова процесса (GP), и явных основных функций, h. Функция ковариации скрытых переменных получает гладкость ответа, и основные функции проектируют входные параметры $x$ в p - размерное пространство признаков.

GP является набором случайных переменных, таких, что любое конечное число их имеет объединенное Распределение Гаусса. Если ${f (x), x \in ℝ^{d}}$ GP, затем, учитывая наблюдения n $x_{1}, x_{2}, ..., x_{n}$ , совместное распределение случайных переменных $f (x_{1}), f (x_{2}), ..., f (x_{n})$ является Гауссовым. GP задан его средней функцией $m (x)$ и функция ковариации, $k (x, x^{'})$ . Таким образом, если ${f (x), x \in ℝ^{d}}$ Гауссов процесс, затем $E (f (x)) = m (x)$ и $C o v [f (x), f (x^{'})] = E [{f (x) - m (x)} {f (x^{'}) - m (x^{'})}] = k (x, x^{'}) .$

Теперь рассмотрите следующую модель.

$h {(x)}^{T} β + f (x),$

где $f (x) ~ G P (0, k (x, x^{'}))$ , это is f (x) от нулевого среднего GP с функцией ковариации, $k (x, x^{'})$ . h (x) является набором основных функций, которые преобразовывают исходный характеристический вектор x в R^d в вектор новой возможности h (x) в R^p. β является p-by-1 вектор коэффициентов основной функции. Эта модель представляет модель GPR. Экземпляр ответа y может быть смоделирован как

$P (y_{i} | f (x_{i}), x_{i}) ~ N (y_{i} | h {(x_{i})}^{T} β + f (x_{i}), σ^{2})$

Следовательно, модель GPR является вероятностной моделью. Существует скрытая переменная f (_xi), введенный для каждого наблюдения $x_{i}$ , который делает модель GPR непараметрической. В векторной форме эта модель эквивалентна

$P (y | f, X) ~ N (y | H β + f, σ^{2} I),$

где

$X = (\begin{matrix} x_{1}^{T} \\ x_{2}^{T} \\ ⋮ \\ x_{n}^{T} \end{matrix}), y = (\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{n} \end{matrix}), H = (\begin{matrix} h (x_{1}^{T}) \\ h (x_{2}^{T}) \\ ⋮ \\ h (x_{n}^{T}) \end{matrix}), f = (\begin{matrix} f (x_{1}) \\ f (x_{2}) \\ ⋮ \\ f (x_{n}) \end{matrix}) .$

Совместное распределение скрытых переменных $f (x_{1}), f (x_{2}), ..., f (x_{n})$ в GPR модель следующие:

$P (f | X) ~ N (f | 0, K (X, X)),$

близко к модели линейной регрессии, где $K (X, X)$ взгляды можно следующим образом:

$K (X, X) = (\begin{matrix} k (x_{1}, x_{1}) & k (x_{1}, x_{2}) & \dots & k (x_{1}, x_{n}) \\ k (x_{2}, x_{1}) & k (x_{2}, x_{2}) & \dots & k (x_{2}, x_{n}) \\ ⋮ & ⋮ & ⋮ & ⋮ \\ k (x_{n}, x_{1}) & k (x_{n}, x_{2}) & \dots & k (x_{n}, x_{n}) \end{matrix}) .$

Функция ковариации $k (x, x^{'})$ обычно параметризован набором параметров ядра или гиперпараметров, $θ$ . Часто $k (x, x^{'})$ записан как $k (x, x^{'} | θ)$ явным образом указать на зависимость от $θ$ .

fitrgp оценивает коэффициенты основной функции, $β$ , шумовое отклонение, $σ^{2}$ , и гиперпараметры, $θ$ , из ядра функционируют из данных в то время как обучение модель GPR. Можно задать основную функцию, ядро (ковариация) функция и начальные значения для параметров.

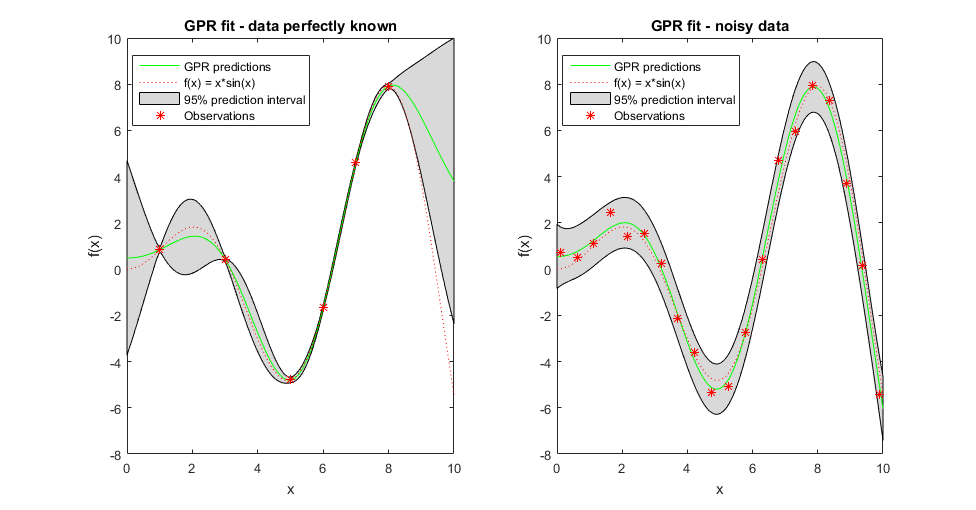
Поскольку модель GPR является вероятностной, возможно вычислить интервалы прогноза с помощью обученной модели (см. predict и resubPredict). Считайте некоторые данные наблюдаемыми от функционального g (x) = x *sin (x) и примите, что они - свободный шум. Подграфик слева в следующем рисунке иллюстрирует наблюдения, подгонку GPR и фактическую функцию. Более реалистично, что наблюдаемые величины не являются точными значениями функции, но шумной реализацией их. Подграфик справа иллюстрирует этот случай. Когда наблюдения являются свободным шумом (как в подграфике слева), подгонка GPR пересекает наблюдения, и стандартное отклонение предсказанного ответа является нулем. Следовательно, вы не видите интервалы прогноза вокруг этих значений.

Можно также вычислить ошибку регрессии обученная модель GPR (см. loss и resubLoss).

Ссылки

[1] Расмуссен, C. E. и К. К. Ай. Уильямс. Гауссовы процессы для машинного обучения. Нажатие MIT. Кембридж, Массачусетс, 2006.

Смотрите также

RegressionGP | fitrgp

Документация