Exponenta Banner

linkage

Агломерационное иерархическое кластерное дерево

свернуть все на странице

Синтаксис

Z = linkage(X)
Z = linkage(X,method)
Z = linkage(X,method,metric)
Z = linkage(X,method,metric,'savememory',value)
Z = linkage(X,method,pdist_inputs)
Z = linkage(y)
Z = linkage(y,method)

Описание

Z = linkage(X) возвращает матричный Z это кодирует дерево, содержащее иерархические кластеры строк матрицы входных данных X.

пример

Z = linkage(X,method) создает дерево с помощью заданного method, который описывает, как измерить расстояние между кластерами. Для получения дополнительной информации смотрите Рычажные устройства.

пример

Z = linkage(X,method,metric) выполняет кластеризацию путем передачи metric к pdist функция, которая вычисляет расстояние между строками X.

пример

Z = linkage(X,method,metric,'savememory',value) использует сохраняющий память алгоритм когда value 'on', и использует стандартный алгоритм когда value 'off'.

пример

Z = linkage(X,method,pdist_inputs) передачи pdist_inputs к pdist функция, которая вычисляет расстояние между строками X. pdist_inputs аргумент состоит из 'seuclidean', 'minkowski', или 'mahalanobis' метрика и дополнительная метрическая опция расстояния.

Z = linkage(y) использует векторное представление y из матрицы расстояния. y или вычисляется pdist или более общая матрица несходства, соответствующая выходному формату pdist.

пример

Z = linkage(y,method) создает дерево с помощью заданного method, который описывает, как измерить расстояние между кластерами.

Примеры

свернуть все

Скрипт Open Live Script

Случайным образом сгенерируйте выборочные данные с 20 000 наблюдений.

rng('default') % For reproducibility
X = rand(20000,3);

Создайте иерархическое кластерное дерево с помощью ward метод рычажного устройства. В этом случае, 'SaveMemory' опция clusterdata функция установлена в 'on' по умолчанию. В общем случае задайте оптимальное значение для 'SaveMemory' на основе размерностей X и доступная память.

Z = linkage(X,'ward');

Кластеризируйте данные максимум в четырех групп и постройте результат.

c = cluster(Z,'Maxclust',4);
scatter3(X(:,1),X(:,2),X(:,3),10,c)

cluster идентифицирует четыре группы в данных.

Скрипт Open Live Script

Найдите максимум трех кластеров в fisheriris набор данных и сравнивает кластерные присвоения цветов к их известной классификации.

Загрузите выборочные данные.

load fisheriris

Создайте иерархическое кластерное дерево с помощью 'average' метод и 'chebychev' метрика.

Z = linkage(meas,'average','chebychev');

Найдите максимум трех кластеров в данных.

T = cluster(Z,'maxclust',3);

Создайте график древовидной схемы Z. Чтобы видеть эти три кластера, используйте 'ColorThreshold' с сокращением на полпути между третьими последними и предпредпоследними рычажными устройствами.

cutoff = median([Z(end-2,3) Z(end-1,3)]);
dendrogram(Z,'ColorThreshold',cutoff)

Отобразите последние две строки Z чтобы видеть, как эти три кластера объединены в один. linkage комбинирует 293-й (синий) кластер с 297-м (красным) кластером, чтобы сформировать 298-й кластер с рычажным устройством 1.7583. linkage затем комбинирует 296-й (зеленый) кластер с 298-м кластером.

lastTwo = Z(end-1:end,:)
lastTwo = 2×3

  293.0000  297.0000    1.7583
  296.0000  298.0000    3.4445

Смотрите, как кластерные присвоения соответствуют трем разновидностям. Например, один из кластеров содержит 50 цветы вторых разновидностей и 40 цветы третьих разновидностей.

crosstab(T,species)
ans = 3×3

     0     0    10
     0    50    40
    50     0     0
Скрипт Open Live Script

Загрузите examgrades набор данных.

load examgrades

Создайте иерархическое дерево с помощью linkage. Используйте 'single' метод и метрика Минковскего с экспонентой 3.

Z = linkage(grades,'single',{'minkowski',3});

Наблюдайте 25-й шаг кластеризации.

Z(25,:)
ans = 1×3

   86.0000  137.0000    4.5307

linkage комбинирует 86-е наблюдение и 137-й кластер, чтобы сформировать кластер индекса 120+25=145, где 120 общее количество наблюдений в grades и 25 номер строки в Z. Кратчайшим расстоянием между 86-м наблюдением и любой из точек в 137-м кластере является 4.5307.

Скрипт Open Live Script

Создайте агломерационное иерархическое кластерное дерево с помощью матрицы несходства.

Возьмите матрицу несходства X и преобразуйте его в векторную форму что linkage принимает при помощи squareform.

X = [0 1 2 3; 1 0 4 5; 2 4 0 6; 3 5 6 0];
y = squareform(X);

Создайте кластерное дерево с помощью linkage с 'complete' метод вычисления расстояния между кластерами. Первые два столбца Z покажите как linkage кластеры объединений. Третий столбец Z дает расстояние между кластерами.

Z = linkage(y,'complete')
Z = 3×3

     1     2     1
     3     5     4
     4     6     6

Создайте график древовидной схемы Z. Ось X соответствует вершинам дерева, и ось Y соответствует расстояниям рычажного устройства между кластерами.

dendrogram(Z)

Входные параметры

свернуть все

Входные данные, заданные как числовая матрица с двумя или больше строками. Строки представляют наблюдения, и столбцы представляют категории или размерности.

Типы данных: single | double

Алгоритм для вычисления расстояния между кластерами, заданными как одно из значений в этой таблице.

МетодОписание
'average'

Невзвешенное среднее расстояние (UPGMA)

'centroid'

Центроидное расстояние (UPGMC), подходящий для Евклидовых расстояний только

'complete'

Самое дальнее расстояние

'median'

Взвешенный центр массового расстояния (WPGMC), подходящий для Евклидовых расстояний только

'single'

Кратчайшее расстояние

'ward'

Внутренний квадрат расстояния (минимальный алгоритм отклонения), подходящий для Евклидовых расстояний только

'weighted'

Средневзвешенное расстояние (WPGMA)

Для получения дополнительной информации об этих методах смотрите Рычажные устройства.

Метрика расстояния, заданная как любая метрика, принята pdist функция. Эти метрики описаны в следующей таблице.

ЗначениеОписание
'euclidean'

Евклидово расстояние (значение по умолчанию).

'squaredeuclidean'

Придал Евклидову расстоянию квадратную форму. (Эта возможность предоставляется для КПД только. Это не удовлетворяет треугольному неравенству.)

'seuclidean'

Стандартизированное Евклидово расстояние. Каждое координатное различие между наблюдениями масштабируется путем деления на соответствующий элемент стандартного отклонения, S = nanstdX. Используйте DistParameter задавать другое значение для S.

'mahalanobis'

Расстояние Mahalanobis с помощью выборочной ковариации X, C = nancovX. Используйте DistParameter задавать другое значение для C, где матричный C симметрично и положительный определенный.

'cityblock'

Расстояние городского квартала.

'minkowski'

Расстояние Минковскего. Экспонента по умолчанию равняется 2. Используйте DistParameter задавать различную экспоненту P, где P значение положительной скалярной величины экспоненты.

'chebychev'

Расстояние Чебычева (максимум координируют различие).

'cosine'

Один минус косинус включенного угла между точками (обработанный как векторы).

'correlation'

Один минус корреляция выборки между точками (обработанный как последовательности значений).

'hamming'

Расстояние Хемминга, которое является процентом координат, которые отличаются.

'jaccard'

Один минус коэффициент Jaccard, который является процентом ненулевых координат, которые отличаются.

'spearman'

Один минус порядковая корреляция демонстрационного Копьеносца между наблюдениями (обработанный как последовательности значений).

@distfun

Пользовательский указатель на функцию расстояния. Функция расстояния имеет форму

function D2 = distfun(ZI,ZJ)
% calculation of distance
...
где

  • ZI 1- n вектор, содержащий одно наблюдение.

  • ZJ m2- n матрица, содержащая несколько наблюдений. distfun должен принять матричный ZJ с произвольным числом наблюдений.

  • D2 m2- 1 вектор расстояний и D2(k) расстояние между наблюдениями ZI и ZJ(k,:).

Если ваши данные не разреженны, можно обычно вычислять расстояние более быстро при помощи встроенного расстояния вместо указателя на функцию.

Для получения дополнительной информации смотрите Метрики Расстояния.

Используйте pdist_inputs вместо metric задавать дополнительный входной параметр DistParameter из pdist для 'seuclidean', 'minkowski', или 'mahalanobis'.

Типы данных: char | string | function_handle

Метрика расстояния и метрическая опция расстояния, заданная как массив ячеек разделенной запятой пары, состоящей из этих двух входных параметров Distance и DistParameter из функционального pdist. Этот аргумент допустим только для определения 'seuclidean', 'minkowski', или 'mahalanobis'.

Пример: {'minkowski',5}

Типы данных: cell

Отметьте для 'savememory' опция, заданная как любой 'on' или 'off'. 'on' установка причин linkage создать кластеры, не вычисляя матрицу расстояния. 'on' установка доступна только когда method 'centroid'медиана, или 'ward' и metric 'euclidean'.

Когда value 'on', linkage время выполнения пропорционально количеству размерностей (количество столбцов X). Когда value 'off', linkage требования к памяти пропорциональны N 2, где N является количеством наблюдений. Лучшее (наименее разовый) устанавливающий, чтобы использовать в value зависит от проблемных размерностей, количества наблюдений и доступной памяти. value по умолчанию установка является грубым приближением оптимальной установки.

Значением по умолчанию является 'on' когда X имеет 20 столбцов или меньше, или компьютер не имеет достаточной памяти, чтобы сохранить матрицу расстояния. В противном случае значением по умолчанию является 'off'.

Пример: 'savememory','on'

Расстояния, заданные как числовой вектор с тем же форматом как выход pdist функция:

  • Вектор-строка из длины m (m – 1)/2, соответствуя парам наблюдений в матрице со строками m

  • Расстояния располагаются в порядке (2,1), (3,1)..., (m, 1), (3,2)..., (m, 2)..., (m, m – 1)),

y может быть более общая матрица несходства, соответствующая выходному формату pdist.

Типы данных: single | double

Выходные аргументы

свернуть все

Агломерационное иерархическое кластерное дерево, возвращенное как числовая матрица. Z (m – 1)-by-3 матрица, где m является количеством наблюдений в исходных данных. Столбцы 1 и 2 Z содержите кластерные индексы, соединенные в парах, чтобы сформировать двоичное дерево. Вершины пронумерованы от 1 до m. Вершины являются одноэлементными кластерами, из которых создаются все более высокие кластеры. Каждый недавно сформированный кластер, соответствуя строке Z(I,:), присвоен индекс m + I. Записи Z(I,1) и Z(I,2) содержите индексы двух кластеров компонента, которые формируют кластерный m + I. m – 1 более высокий кластер соответствует внутренним узлам кластеризирующегося дерева. Z(I,3) содержит расстояние рычажного устройства между этими двумя кластерами, объединенными в строке Z(I,:).

Например, рассмотрите создание дерева с 30 начальными узлами. Предположим, что кластер 5 и кластер 7 объединены на шаге 12, и что расстояние между ними на том шаге 1.5. Затем Z(12,:) [5 7 1.5]. Недавно сформированный кластер имеет индекс 12 + 30 = 42. Если кластер 42 появляется в более поздней строке, то функция комбинирует кластер, созданный на шаге 12 в больший кластер.

Типы данных: single | double

Больше о

свернуть все

Рычажные устройства

Рычажное устройство является расстоянием между двумя кластерами.

Следующее обозначение описывает рычажные устройства, используемые различными методами:

  • Кластерный r формируется из кластеров p и q.

  • n r является количеством объектов в кластерном r.

  • x ri является i th объект в кластерном r.

  • Одно рычажное устройство, также названное самым близким соседом, использует наименьшее расстояние между объектами в этих двух кластерах.

    d(r,s)=min(dist(xri,xsj)),i∈(i,...,nr),j∈(1,...,ns)

  • Полное рычажное устройство, также названное дальше всего, граничит, использует самое большое расстояние между объектами в этих двух кластерах.

    d(r,s)=max (dist(xri,xsj)),i∈(1,...,nr),j∈(1,...,ns)

  • Среднее рычажное устройство использует среднее расстояние между всеми парами объектов в любых двух кластерах.

    d(r,s)=1nrns∑i=1nr∑j=1nsdist(xri,xsj)

  • Центроидное рычажное устройство использует Евклидово расстояние между центроидами этих двух кластеров.

    d(r,s)=‖x¯r−x¯s‖2,

    где

    x¯r=1nr∑i=1nrxri

  • Среднее рычажное устройство использует Евклидово расстояние между взвешенными центроидами этих двух кластеров.

    d(r,s)=‖x˜r−x˜s‖2,

    где x˜r и x˜s взвешенные центроиды для кластеров r и s. Если кластерный r был создан путем объединения кластеров p и q, x˜r задан рекурсивно как

    x˜r=12(x˜p+x˜q)

  • Рычажное устройство опеки использует инкрементную сумму квадратов, то есть, увеличение общей суммы квадратов в кластере в результате присоединения двух кластеров. Сумма квадратов в кластере задана как сумма квадратов расстояний между всеми объектами в кластере и центроиде кластера. Метрика суммы квадратов эквивалентна следующей метрике расстояния d (r, s), который является формулой linkage использование.

    d(r,s)=2nrns(nr+ns)‖x¯r−x¯s‖2,

    где

    • ‖‖2 Евклидово расстояние.

    • x¯r и x¯s центроиды кластеров r и s.

    • nr и ns являются числом элементов в кластерах r и s.

    В некоторых ссылках рычажное устройство Уорда не использует фактор 2 умножающихся nrns. linkage функционируйте использует этот фактор так, чтобы расстояние между двумя одноэлементными кластерами совпало с Евклидовым расстоянием.

  • Средневзвешенное рычажное устройство использует рекурсивное определение в расстоянии между двумя кластерами. Если кластерный r был создан путем объединения кластеров, p и q, расстояние между r и другим кластерным s заданы как среднее значение расстояния между p и s и расстояния между q и s.

    d(r,s)=(d(p,s)+d(q,s))2

Советы

  • Вычисление linkage(y) может быть медленным когда y векторное представление матрицы расстояния. Для 'centroid'медиана, и 'ward' методы, linkage проверки, ли y Евклидово расстояние. Избегайте этой длительной проверки путем передачи в X вместо y.

  • 'centroid' и 'median' методы могут произвести кластерное дерево, которое не является монотонным. Этот результат происходит, когда расстояние от объединения двух кластеров, r и s, к третьему кластеру меньше расстояния между r и s. В этом случае, в древовидной схеме, чертившей с ориентацией по умолчанию, путь от листа до корневого узла делает некоторые нисходящие шаги. Чтобы избежать этого результата, используйте другой метод. Этот рисунок показывает немонотонное кластерное дерево.

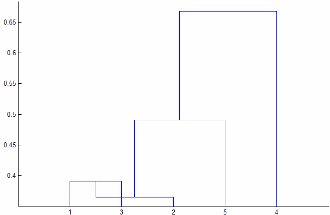
    В этом случае к кластеру 1 и кластеру 3 соединяют в новый кластер, и расстояние между этим новым кластером и кластером 2 меньше расстояния между кластером 1 и кластером 3. Результатом является немонотонное дерево.

  • Можно обеспечить выход Z к другим функциям включая dendrogram отобразить дерево, cluster присваивать точки кластерам, inconsistent вычислить противоречивые меры и cophenet вычислить cophenetic коэффициент корреляции.

Смотрите также

| | | | | | | |

Темы

Представлено до R2006a

Документация Statistics and Machine Learning Toolbox
Поддержка