Неклассическое многомерное масштабирование
Y = mdscale(D,p)
[Y,stress] = mdscale(D,p)
[Y,stress,disparities] = mdscale(D,p)
[...] = mdscale(D,p,'Name',value)
Y = mdscale(D,p) выполняет неметрическое многомерное масштабирование на n на n матрице несходства D, и возвращает Y, настройка n точек (строки) в p размерности (столбцы). Евклидовы расстояния между точками в Y аппроксимируйте монотонное преобразование соответствующих несходств в D. По умолчанию, mdscale использование Краскэл нормировало stress1 критерий.
Можно задать D или как полная n на n матрица, или в верхней треугольной форме той, которая выводится pdist. Полная матрица несходства должна быть действительной и симметричной, и еще иметь нули вдоль диагональных и неотрицательных элементов везде. Матрица несходства в верхней треугольной форме должна иметь действительные, неотрицательные записи. mdscale обработки NaNгрешивший как отсутствующие значения, и игнорирует те элементы. Inf не принят.
Можно также задать D как полная матрица подобия, с единицами по диагонали и всем другим элементам меньше чем один. mdscale преобразовывает матрицу подобия к матрице несходства таким способом который расстояния между точками, возвращенными в Y аппроксимированный sqrt(1-D). Чтобы использовать различное преобразование, преобразуйте общие черты до вызова mdscale.
[Y,stress] = mdscale(D,p) возвращает минимизированное напряжение, т.е. напряжение, оцененное в Y.
[Y,stress,disparities] = mdscale(D,p) возвращает несоизмеримости, то есть, монотонное преобразование несходств D.
[...] = mdscale(D,p,' задает один или несколько дополнительное название параметра / пары значения, которые управляют более подробной информацией Name',value)mdscale. Задайте Name в одинарных кавычках. Доступные параметры
Criterion— Критерий качества подгонки, чтобы минимизировать. Это также определяет тип масштабирования, или неметрика или метрика, тот mdscale выполняет. Выбор для неметрического масштабирования:
'stress' — Напряжение, нормированное суммой квадратов разделять знаками препинания расстояний, также известных stress1. Это значение по умолчанию.
'sstress' — Напряжение в квадрате, нормированное с суммой 4-х степеней разделять знаками препинания расстояний.
Выбор для метрического масштабирования:
'metricstress' — Подчеркните, нормированный с суммой квадратов несходств.
'metricsstress' — Напряжение в квадрате, нормированное с суммой 4-х степеней несходств.
'sammon' — Нелинейный критерий отображения Сэммона. Недиагональные несходства должны быть строго положительными с этим критерием.
'strain' — Критерий, эквивалентный используемому в классическом многомерном масштабировании.
Weights — Матрица A или вектор тот же размер как D, содержа неотрицательные веса несходства. Можно использовать их, чтобы взвесить вклад соответствующих элементов D в вычислении и минимизации напряжения. Элементы D соответствующий, чтобы обнулить веса эффективно проигнорированы.
Когда вы задаете веса как полную матрицу, ее диагональные элементы проигнорированы и не оказывают влияния, начиная с соответствующих диагональных элементов D не вводите в вычисление напряжения.
Start — Метод раньше выбирал начальную настройку точек для Y. Выбор
'cmdscale' — Используйте классическое многомерное решение для масштабирования. Это значение по умолчанию. 'cmdscale' не допустимо, когда существуют нулевые веса.
'random' — Выберите местоположения случайным образом из соответственно масштабированного p-dimensional нормального распределения с некоррелироваными координатами.
N-by-p матрица начальных местоположений, где n является размером матричного D и p количество столбцов выходной матрицы Y. В этом случае можно передать в [] для p и mdscale выводит p от второго измерения матрицы. Можно также предоставить трехмерный массив, подразумевая значение для 'Replicates' от третьей размерности массива.
Replicates — Число раз, чтобы повторить масштабирование, каждого с новой начальной настройкой. Значением по умолчанию является 1.
Options — Опции для итеративного алгоритма раньше минимизировали подходящий критерий. Передайте в структуре опций, созданной statset. Например,
opts = statset(param1,val1,param2,val2, ...); [...] = mdscale(...,'Options',opts)
Выбор statset параметры
'Display' — Level of display выводится. Выбором является 'off' (значение по умолчанию), 'iter', и 'final'.
'MaxIter' — Максимальное количество итераций позволено. Значением по умолчанию является 200.
'TolFun' — Допуск завершения к критерию напряжения и его градиенту. Значением по умолчанию является 1e-4.
'TolX'— Допуск завершения к размеру шага местоположения настройки. Значением по умолчанию является 1e-4.
load cereal.mat
X = [Calories Protein Fat Sodium Fiber ...
Carbo Sugars Shelf Potass Vitamins];
% Take a subset from a single manufacturer.
X = X(strcmp('K',cellstr(Mfg)),:);
% Create a dissimilarity matrix.
dissimilarities = pdist(X);
% Use non-metric scaling to recreate the data in 2D,
% and make a Shepard plot of the results.
[Y,stress,disparities] = mdscale(dissimilarities,2);
distances = pdist(Y);
[dum,ord] = sortrows([disparities(:) dissimilarities(:)]);
plot(dissimilarities,distances,'bo', ...
dissimilarities(ord),disparities(ord),'r.-');
xlabel('Dissimilarities'); ylabel('Distances/Disparities')
legend({'Distances' 'Disparities'},'Location','NW');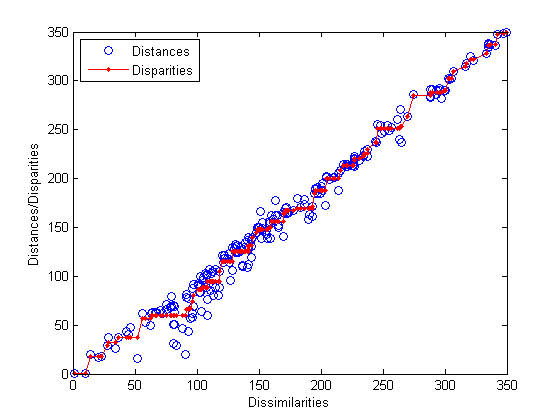
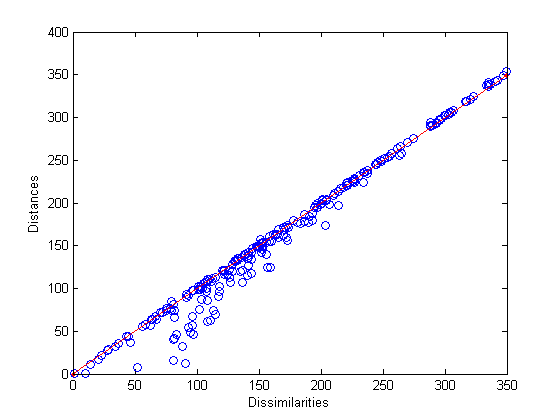
% Do metric scaling on the same dissimilarities.
figure
[Y,stress] = ...
mdscale(dissimilarities,2,'criterion','metricsstress');
distances = pdist(Y);
plot(dissimilarities,distances,'bo', ...
[0 max(dissimilarities)],[0 max(dissimilarities)],'r.-');
xlabel('Dissimilarities'); ylabel('Distances')