Полиномиальные доверительные интервалы
Y = polyconf(p,X)
[Y,DELTA] = polyconf(p,X,S)
[Y,DELTA] = polyconf(p,X,S,param1,val1,param2,val2,...)
Y = polyconf(p,X) оценивает полиномиальный p в значениях в XP вектор коэффициентов в убывающих степенях.
[Y,DELTA] = polyconf(p,X,S) берет выходные параметры p и S от polyfit и генерирует 95% интервалов прогноза Y ± DELTA для новых наблюдений в значениях в X.
[Y,DELTA] = polyconf(p,X,S, задает дополнительное название параметра / пары значения, выбранные из следующего списка.param1,val1,param2,val2,...)
| Параметр | Значение |
|---|---|
'alpha' | Значение между 0 и 1 определением доверительного уровня |
'mu' | Двухэлементный вектор, содержащий центрирование и масштабные коэффициенты. При использовании этой опции, |
'predopt' | Любой |
'simopt' | Любой |
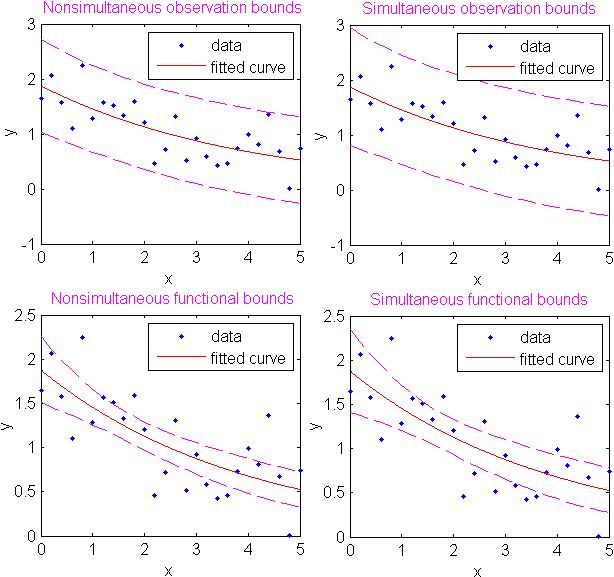
'predopt' и 'simopt' параметры могут быть изучены в терминах следующих функций:
p (x) — неизвестная средняя функция оценивается подгонкой
l (x) — более низкая доверительная граница
u (x) — верхняя доверительная граница
Предположим, что вы делаете новое наблюдение y n +1 в x n +1, так, чтобы
y n +1 (x n +1) = p (x n +1) + ε n +1
По умолчанию, интервал [l n +1 (x n +1), u n +1 (x n +1)] является 95%-й доверительной границей на y n +1 (x n +1).
Следующие комбинации 'predopt' и 'simopt' параметры позволяют вам задавать другие границы.
'simopt' | 'predopt' | Ограниченная величина |
|---|---|---|
'off' | 'observation' | y n +1 (x n +1) (значение по умолчанию) |
'off' | 'curve' | p (x n +1) |
'on' | 'observation' | y n +1 (x), для всего x |
'on' | 'curve' | p (x), для всего x |
В общем случае 'observation' интервалы более широки, чем 'curve' интервалы, из-за дополнительной неопределенности в предсказании нового значения ответа (кривая плюс случайные ошибки). Аналогично, одновременные интервалы более широки, чем неодновременные интервалы из-за дополнительной неопределенности в ограничении значений для всех предикторов x.
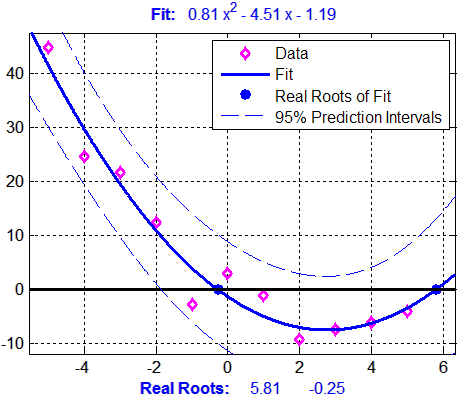
Этот пример использует код от функции, взятой в качестве примера, документации polydemo, и вызывает функцию, взятую в качестве примера, документации polystr преобразовывать вектор коэффициентов p в текст для многочленного выражения, отображенного в заголовке фигуры. Это комбинирует функции polyfitpolyvalкорни, и polyconf произвести отформатированное отображение данных с аппроксимацией полиномом.
Файлы документации Statistics and Machine Learning Toolbox™ в качестве примера расположены в \help\toolbox\stats\examples подкаталог вашей корневой папки MATLAB® (matlabroot). Этот подкаталог не находится на пути MATLAB при установке. Чтобы использовать файлы в этом подкаталоге, любой добавляет подкаталог в путь MATLAB (addpath) или сделайте подкаталог вашей текущей рабочей папкой (cd).
Отобразите симулированные данные с квадратичным трендом, подходящим квадратичным полиномом, и 95% интервалов прогноза для новых наблюдений:
xdata = -5:5;
ydata = xdata.^2 - 5*xdata - 3 + 5*randn(size(xdata));
degree = 2; % Degree of the fit
alpha = 0.05; % Significance level
% Compute the fit and return the structure used by
% POLYCONF.
[p,S] = polyfit(xdata,ydata,degree);
% Compute the real roots and determine the extent of the
% data.
r = roots(p)'; % Roots as a row vector.
real_r = r(imag(r) == 0); % Real roots.
% Assure that the data are row vectors.
xdata = reshape(xdata,1,length(xdata));
ydata = reshape(ydata,1,length(ydata));
% Extent of the data.
mx = min([real_r,xdata]);
Mx = max([real_r,xdata]);
my = min([ydata,0]);
My = max([ydata,0]);
% Scale factors for plotting.
sx = 0.05*(Mx-mx);
sy = 0.05*(My-my);
% Plot the data, the fit, and the roots.
hdata = plot(xdata,ydata,'md','MarkerSize',5,...
'LineWidth',2);
hold on
xfit = mx-sx:0.01:Mx+sx;
yfit = polyval(p,xfit);
hfit = plot(xfit,yfit,'b-','LineWidth',2);
hroots = plot(real_r,zeros(size(real_r)),...
'bo','MarkerSize',5,...
'LineWidth',2,...
'MarkerFaceColor','b');
grid on
plot(xfit,zeros(size(xfit)),'k-','LineWidth',2)
axis([mx-sx Mx+sx my-sy My+sy])
% Add prediction intervals to the plot.
[Y,DELTA] = polyconf(p,xfit,S,'alpha',alpha);
hconf = plot(xfit,Y+DELTA,'b--');
plot(xfit,Y-DELTA,'b--')
% Display the polynomial fit and the real roots.
approx_p = round(100*p)/100; % Round for display.
htitle = title(['{\bf Fit: }',...
texlabel(polystr(approx_p))]);
set(htitle,'Color','b')
approx_real_r = round(100*real_r)/100; % Round for display.
hxlabel = xlabel(['{\bf Real Roots: }',...
num2str(approx_real_r)]);
set(hxlabel,'Color','b')
% Add a legend.
legend([hdata,hfit,hroots,hconf],...
'Data','Fit','Real Roots of Fit',...
'95% Prediction Intervals')