Квантили набора данных
Y = quantile(X,p)X для интегральной вероятности или вероятностей p в интервале [0,1].
Если X вектор, затем Y скаляр или вектор, имеющий ту же длину как p.
Если X матрица, затем Y вектор-строка или матрица где количество строк Y равно длине p.
Для многомерных массивов, quantile действует по первому неодноэлементному измерению X.
Y = quantile(X,N)N равномерно распределенные интегральные вероятности (1 / (N + 1), 2 / (N + 1)..., NN + 1)) для целочисленного N>1.
Если X вектор, затем Y скаляр или вектор с длиной N.
Если X матрица, затем Y матрица где количество строк Y равно N.
Для многомерных массивов, quantile действует по первому неодноэлементному измерению X.
Y = quantile(___,vecdim)vecdim для любого из первых двух синтаксисов. Например, если X матрица, затем quantile(X,0.5,[1 2]) возвращает 0,5 квантиля всех элементов X потому что каждый элемент матрицы содержится в срезе массивов, заданном размерностями 1 и 2.
Вычислите квантили набора данных для заданных вероятностей.
Сгенерируйте набор данных размера 10.
rng('default'); % for reproducibility x = normrnd(0,1,1,10)
x = 1×10
0.5377 1.8339 -2.2588 0.8622 0.3188 -1.3077 -0.4336 0.3426 3.5784 2.7694
Вычислите 0,3 квантиля.
y = quantile(x,0.30)
y = -0.0574
Вычислите квантили для интегральных вероятностей 0.025, 0.25, 0.5, 0.75, и 0.975.
y = quantile(x,[0.025 0.25 0.50 0.75 0.975])
y = 1×5
-2.2588 -0.4336 0.4401 1.8339 3.5784
Вычислите квантили набора данных для данного количества квантилей.
Сгенерируйте набор данных размера 10.
rng('default'); % for reproducibility x = normrnd(0,1,1,10)
x = 1×10
0.5377 1.8339 -2.2588 0.8622 0.3188 -1.3077 -0.4336 0.3426 3.5784 2.7694
Вычислите четыре равномерно расположенных с интервалами квантиля.
y = quantile(x,4)
y = 1×4
-0.8706 0.3307 0.6999 2.3017
Используя y = quantile(x,[0.2,0.4,0.6,0.8]) другой путь состоит в том, чтобы возвратить четыре равномерно расположенных с интервалами квантиля.
Вычислите квантили вдоль столбцов и строк матрицы данных для заданных вероятностей.
Сгенерируйте 4 6 матрицу данных.
rng default % For reproducibility X = normrnd(0,1,4,6)
X = 4×6
0.5377 0.3188 3.5784 0.7254 -0.1241 0.6715
1.8339 -1.3077 2.7694 -0.0631 1.4897 -1.2075
-2.2588 -0.4336 -1.3499 0.7147 1.4090 0.7172
0.8622 0.3426 3.0349 -0.2050 1.4172 1.6302
Вычислите 0,3 квантиля для каждого столбца X dim = 1).
y = quantile(X,0.3,1)
y = 1×6
-0.3013 -0.6958 1.5336 -0.1056 0.9491 0.1078
quantile возвращает вектор-строку y при вычислении одного квантиля для каждого столбца матрицы. Например, -0.3013 0,3 квантиля первого столбца X с элементами (0.5377, 1.8339,-2.2588, 0.8622). Поскольку значение по умолчанию dim 1, можно возвратить тот же результат с y = quantile(X,0.3).
Вычислите 0,3 квантиля для каждой строки X dim = 2).
y = quantile(X,0.3,2)
y = 4×1
0.3844
-0.8642
-1.0750
0.4985
quantile возвращает вектор-столбец y при вычислении одного квантиля для каждой строки матрицы. Например, 0.3844 0,3 квантиля первой строки X с элементами (0.5377, 0.3188, 3.5784, 0.7254,-0.1241, 0.6715).
Вычислите равномерно распределенные квантили вдоль столбцов и строк матрицы данных.
Сгенерируйте 6 10 матрицу данных.
rng('default'); % for reproducibility X = unidrnd(10,6,7)
X = 6×7
9 3 10 8 7 8 7
10 6 5 10 8 1 4
2 10 9 7 8 3 10
10 10 2 1 4 1 1
7 2 5 9 7 1 5
1 10 10 10 2 9 4
Вычислите три равномерно расположенных с интервалами квантиля для каждого столбца X dim = 1).
y = quantile(X,3,1)
y = 3×7
2.0000 3.0000 5.0000 7.0000 4.0000 1.0000 4.0000
8.0000 8.0000 7.0000 8.5000 7.0000 2.0000 4.5000
10.0000 10.0000 10.0000 10.0000 8.0000 8.0000 7.0000
Каждый столбец матричного y соответствует трем равномерно расположенным с интервалами квантилям каждого столбца матричного X. Например, первый столбец y с элементами (2, 8, 10) имеет квантили для первого столбца X с элементами (9, 10, 2, 10, 7, 1). y = quantile(X,3) дает тот же ответ потому что значение по умолчанию dim 1.
Вычислите три равномерно расположенных с интервалами квантиля для каждой строки X dim = 2).
y = quantile(X,3,2)
y = 6×3
7.0000 8.0000 8.7500
4.2500 6.0000 9.5000
4.0000 8.0000 9.7500
1.0000 2.0000 8.5000
2.7500 5.0000 7.0000
2.5000 9.0000 10.0000
Каждая строка матричного y соответствует трем равномерно расположенным с интервалами квантилям каждой строки матричного X. Например, первая строка y с элементами (7, 8, 8.75) имеет квантили для первой строки X с элементами (9, 3, 10, 8, 7, 8, 7).
Вычислите квантили многомерного массива для заданных вероятностей при помощи 'all' и vecdim входные параметры.
Создайте 3 5 2 массивами X. Задайте вектор вероятностей p.
X = reshape(1:30,[3 5 2])
X =
X(:,:,1) =
1 4 7 10 13
2 5 8 11 14
3 6 9 12 15
X(:,:,2) =
16 19 22 25 28
17 20 23 26 29
18 21 24 27 30
p = [0.25 0.75];
Вычислите 0,25 и 0,75 квантиля всех элементов в X.
Yall = quantile(X,p,'all')Yall = 2×1
8
23
Yall(1) 0,25 квантиля X, и Yall(2) 0,75 квантиля X.
Вычислите 0,25 и 0,75 квантиля для каждой страницы X путем определения размерностей 1 и 2 как операционные размерности.
Ypage = quantile(X,p,[1 2])
Ypage =
Ypage(:,:,1) =
4.2500
11.7500
Ypage(:,:,2) =
19.2500
26.7500
Например, Ypage(1,1,1) 0,25 квантиля первой страницы X, и Ypage(2,1,1) 0,75 квантиля первой страницы X.
Вычислите 0,25 и 0,75 квантиля элементов в каждом X(i,:,:) срез путем определения размерностей 2 и 3 как операционные размерности.
Yrow = quantile(X,p,[2 3])
Yrow = 3×2
7 22
8 23
9 24
Например, Yrow(3,1) 0,25 квантиля элементов в X(3,:,:), и Yrow(3,2) 0,75 квантиля элементов в X(3,:,:).
Найдите медиану и квартили вектора, x, с четным числом элементов.
Введите данные.
x = [2 5 6 10 11 13]
x = 1×6
2 5 6 10 11 13
Вычислите медиану x.
y = quantile(x,0.50)
y = 8
Вычислите квартили x.
y = quantile(x,[0.25, 0.5, 0.75])
y = 1×3
5 8 11
Используя y = quantile(x,3) другой путь состоит в том, чтобы вычислить квартили x.
Эти результаты могут отличаться, чем определения учебника потому что quantile Линейная интерполяция использования, чтобы найти медиану и квартили.
Найдите медиану и квартили вектора, x, с нечетным числом элементов.
Введите данные.
x = [2 4 6 8 10 12 14]
x = 1×7
2 4 6 8 10 12 14
Найдите медиану x.
y = quantile(x,0.50)
y = 8
Найдите квартили x.
y = quantile(x,[0.25, 0.5, 0.75])
y = 1×3
4.5000 8.0000 11.5000
Используя y = quantile(x,3) другой путь состоит в том, чтобы вычислить квартили x.
Эти результаты могут отличаться, чем определения учебника потому что quantile Линейная интерполяция использования, чтобы найти медиану и квартили.
Вычислите точные и аппроксимированные квантили высокого вектор-столбца для данной вероятности.
Когда вы выполняете вычисления на длинных массивах, MATLAB® использует любого параллельный пул (значение по умолчанию, если у вас есть Parallel Computing Toolbox™), или локальный сеанс работы с MATLAB. Если вы хотите запустить пример с помощью локального сеанса работы с MATLAB, когда у вас есть Parallel Computing Toolbox, можно изменить глобальную среду выполнения при помощи mapreducer функция.
Создайте datastore для airlinesmall набор данных. Обработайте 'NA' значения как недостающие данные так, чтобы datastore заменяет их на NaN значения. Задайте, чтобы работать с ArrTime переменная.
ds = datastore('airlinesmall.csv','TreatAsMissing','NA',... 'SelectedVariableNames','ArrTime');
Составьте длинную таблицу сверху datastore и извлеките данные из длинной таблицы в высокий вектор.
t = tall(ds) % Tall tableStarting parallel pool (parpool) using the 'local' profile ...
Connected to the parallel pool (number of workers: 12).
t =
Mx1 tall table
ArrTime
_______
735
1124
2218
1431
746
1547
1052
1134
:
:
x = t{:,:} % Tall vectorx =
Mx1 tall double column vector
735
1124
2218
1431
746
1547
1052
1134
:
:
Вычислите точный квантиль x для p = 0.5. Поскольку X высокий вектор-столбец и p скаляр, quantile возвращает точное значение квантиля по умолчанию.
p = 0.5; % Cumulative probability
yExact = quantile(x,p)yExact =
tall double
?
Вычислите аппроксимированный квантиль x для p = 0.5. Задайте 'Method','approximate' использовать алгоритм аппроксимации на основе T-обзора для вычисления квантилей.
yApprox = quantile(x,p,'Method','approximate')
yApprox =
MxNx... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Оцените длинные массивы и загрузите результаты в память при помощи gather.
[yExact,yApprox] = gather(yExact,yApprox)
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 4: Completed in 4.6 sec - Pass 2 of 4: Completed in 1 sec - Pass 3 of 4: Completed in 1.6 sec - Pass 4 of 4: Completed in 1.3 sec Evaluation completed in 11 sec
yExact = 1522
yApprox = 1.5220e+03
Значения аппроксимированного квантиля и точного квантиля являются тем же самым к этим четырем показанным цифрам.
Вычислите точные и аппроксимированные квантили высокой матрицы для заданных интегральных вероятностей по различным измерениям.
Когда вы выполняете вычисления на длинных массивах, MATLAB® использует любого параллельный пул (значение по умолчанию, если у вас есть Parallel Computing Toolbox™), или локальный сеанс работы с MATLAB. Если вы хотите запустить пример с помощью локального сеанса работы с MATLAB, когда у вас есть Parallel Computing Toolbox, можно изменить глобальную среду выполнения при помощи mapreducer функция.
Создайте высокий матричный X содержа подмножество переменных из airlinesmall набор данных. Смотрите Квантили Высокого Вектора для Данной Вероятности для получения дополнительной информации о шагах, чтобы извлечь данные из длинного массива.
varnames = {'ArrDelay','ArrTime','DepTime','ActualElapsedTime'}; % Subset of variables in the data set
ds = datastore('airlinesmall.csv','TreatAsMissing','NA',...
'SelectedVariableNames',varnames); % Datastore
t = tall(ds); % Tall tableStarting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 12).
X = t{:,varnames} % Tall matrixX =
Mx4 tall double matrix
8 735 642 53
8 1124 1021 63
21 2218 2055 83
13 1431 1332 59
4 746 629 77
59 1547 1446 61
3 1052 928 84
11 1134 859 155
: : : :
: : : :
При работе по измерению, которое не является 1, quantile функция вычисляет точные квантили только, так, чтобы она могла выполнить расчет эффективно с помощью основанного на сортировке алгоритма (см. Алгоритмы) вместо алгоритма аппроксимации на основе T-обзора.
Вычислите точные квантили X вдоль второго измерения для интегральных вероятностей 0.25, 0.5, и 0.75.
p = [0.25 0.50 0.75]; % Vector of cumulative probabilities
Yexact = quantile(X,p,2)Yexact =
MxNx... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Когда функция действует по первому измерению и p вектор интегральных вероятностей, необходимо использовать алгоритм аппроксимации на основе t-обзора, чтобы вычислить квантили. Используя основанный на сортировке алгоритм, чтобы найти квантили по первому измерению длинного массива в вычислительном отношении интенсивно.
Вычислите аппроксимированные квантили X по первому измерению для интегральных вероятностей 0.25, 0.5, и 0.75. Поскольку размерность по умолчанию равняется 1, вы не должны задавать значение для dim.
Yapprox = quantile(X,p,'Method','approximate')
Yapprox =
MxNx... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Оцените длинные массивы и загрузите результаты в память при помощи gather.
[Yexact,Yapprox] = gather(Yexact,Yapprox);
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 6.1 sec Evaluation completed in 7.6 sec
Покажите первые пять строк точных квантилей X (вдоль второго измерения) для интегральных вероятностей 0.25, 0.5, и 0.75.
Yexact(1:5,:)
ans = 5×3
103 ×
0.0305 0.3475 0.6885
0.0355 0.5420 1.0725
0.0520 1.0690 2.1365
0.0360 0.6955 1.3815
0.0405 0.3530 0.6875
Каждая строка матричного Yexact содержит три квантиля соответствующей строки в X. Например, 30.5, 347.5, и 688.5 0.25, 0.5, и 0,75 квантиля, соответственно, первой строки в X.
Покажите аппроксимированные квантили X (по первому измерению) для интегральных вероятностей 0.25, 0.5, и 0.75.
Yapprox
Yapprox = 3×4
103 ×
-0.0070 1.1149 0.9322 0.0700
0 1.5220 1.3350 0.1020
0.0110 1.9180 1.7400 0.1510
Каждый столбец матричного Yapprox соответствует этим трем квантилям для каждого столбца матричного X. Например, первый столбец Yapprox с элементами (–7, 0, 11) содержит квантили для первого столбца X.
Вычислите точные и аппроксимированные квантили по различным измерениям высокой матрицы для N равномерно распределенные интегральные вероятности.
Когда вы выполняете вычисления на длинных массивах, MATLAB® использует любого параллельный пул (значение по умолчанию, если у вас есть Parallel Computing Toolbox™), или локальный сеанс работы с MATLAB. Если вы хотите запустить пример с помощью локального сеанса работы с MATLAB, когда у вас есть Parallel Computing Toolbox, можно изменить глобальную среду выполнения при помощи mapreducer функция.
Создайте высокий матричный X содержа подмножество переменных из airlinesmall набор данных. Смотрите Квантили Высокого Вектора для Данной Вероятности для получения дополнительной информации о шагах, чтобы извлечь данные из длинного массива.
varnames = {'ArrDelay','ArrTime','DepTime','ActualElapsedTime'}; % Subset of variables in the data set
ds = datastore('airlinesmall.csv','TreatAsMissing','NA',...
'SelectedVariableNames',varnames); % Datastore
t = tall(ds); % Tall tableStarting parallel pool (parpool) using the 'local' profile ... Connected to the parallel pool (number of workers: 12).
X = t{:,varnames}X =
Mx4 tall double matrix
8 735 642 53
8 1124 1021 63
21 2218 2055 83
13 1431 1332 59
4 746 629 77
59 1547 1446 61
3 1052 928 84
11 1134 859 155
: : : :
: : : :
Чтобы найти равномерно распределенные квантили по первому измерению, необходимо использовать алгоритм аппроксимации на основе T-обзора. Используя основанный на сортировке алгоритм (см. Алгоритмы), чтобы найти квантили по первому измерению длинного массива в вычислительном отношении интенсивно.
Вычислите три равномерно расположенных с интервалами квантиля по первому измерению X. Поскольку размерность по умолчанию равняется 1, вы не должны задавать значение для dim. Задайте 'Method','approximate' использовать алгоритм аппроксимации.
N = 3; % Number of quantiles Yapprox = quantile(X,N,'Method','approximate')
Yapprox =
MxNx... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Найти равномерно распределенные квантили по любому другому измерению (dim не 1), quantile вычисляет точные квантили только, так, чтобы это могло выполнить расчет эффективно при помощи основанного на сортировке алгоритма.
Вычислите три равномерно расположенных с интервалами квантиля вдоль второго измерения X. Поскольку dim не 1, quantile возвращает точные квантили по умолчанию.
Yexact = quantile(X,N,2)
Yexact =
MxNx... tall double array
? ? ? ...
? ? ? ...
? ? ? ...
: : :
: : :
Оцените длинные массивы и загрузите результаты в память при помощи gather.
[Yapprox,Yexact] = gather(Yapprox,Yexact);
Evaluating tall expression using the Parallel Pool 'local': - Pass 1 of 1: Completed in 5.9 sec Evaluation completed in 7.4 sec
Покажите аппроксимированные квантили X (по первому измерению) для трех равномерно расположенных с интервалами интегральных вероятностей.
Yapprox
Yapprox = 3×4
103 ×
-0.0070 1.1149 0.9322 0.0700
0 1.5220 1.3350 0.1020
0.0110 1.9180 1.7400 0.1510
Каждый столбец матричного Yapprox соответствует трем равномерно расположенным с интервалами квантилям для каждого столбца матричного X. Например, первый столбец Yapprox с элементами (–7, 0, 11) содержит квантили для первого столбца X.
Покажите первые пять строк точных квантилей X (вдоль второго измерения) для трех равномерно расположенных с интервалами интегральных вероятностей.
Yexact(1:5,:)
ans = 5×3
103 ×
0.0305 0.3475 0.6885
0.0355 0.5420 1.0725
0.0520 1.0690 2.1365
0.0360 0.6955 1.3815
0.0405 0.3530 0.6875
Каждая строка матричного Yexact содержит три равномерно расположенных с интервалами квантиля соответствующей строки в X. Например, 30.5, 347.5, и 688.5 0.25, 0.5, и 0,75 квантиля, соответственно, первой строки в X.
X — Входные данныеВходные данные, заданные как вектор или массив.
Типы данных: double | single
p — Интегральные вероятностиИнтегральные вероятности, для которых можно вычислить квантили, заданные как скаляр или вектор скаляров от 0 до 1.
Пример: 0.3
Пример: [0.25, 0.5, 0.75]
Пример: (0:0.25:1)
Типы данных: double | single
N — Количество квантилейКоличество квантилей, чтобы вычислить, заданный как положительное целое число. quantile возвращает N квантили, которые делят набор данных на равномерно распределенный N+1 сегмент.
Типы данных: double | single
dim — Размерность Размерность, вдоль который квантили матричного X требуются, задаются как положительное целое число. Например, для матричного X, когда dim = 1, quantile возвращает квантиль (квантили) столбцов X; когда dim = 2, quantile возвращает квантиль (квантили) строк X. Для многомерного массива X, длина dimразмерность th Y совпадает с длиной p.
Типы данных: single | double
vecdim — Вектор размерностейВектор размерностей, заданных как положительный целочисленный вектор. Каждый элемент vecdim представляет размерность входного массива X. В самой маленькой заданной операционной размерности (то есть, размерность min(vecdim)), выход Y имеет длину, равную количеству квантилей, которые требуют (любой N или length(p)). В каждой из остающихся операционных размерностей, Y имеет длину 1. Другие длины размерности являются тем же самым для X и Y.
Например, считайте 2 3х3 массивом X с p = [0.2 0.4 0.6 0.8]. В этом случае, quantile(X,p,[1 2]) возвращает массив, где каждая страница массива содержит 0.2, 0.4, 0.6, и 0,8 квантиля элементов на соответствующей странице X. Поскольку 1 и 2 операционные размерности, с min([1 2]) = 1 и length(p) = 4, выход является 4 1 3 массивами.
Типы данных: single | double
method — Метод для вычисления квантилей'exact' (значение по умолчанию) | 'approximate'Метод для вычисления квантилей, заданных как 'exact' или 'approximate'. По умолчанию, quantile возвращает точные квантили путем реализации алгоритма, который использует сортировку. Можно задать 'method','approximate' для quantile возвратить аппроксимированные квантили путем реализации алгоритма, который использует T-обзор.
Типы данных: char | string
Y — КвантилиКвантили вектора данных или массива, возвращенного как скаляр или массив для один или несколько значений интегральных вероятностей.
Если X вектор, затем Y скаляр или вектор с той же длиной как количество квантилей, которые требуют (N или length(p)). Y(i) содержит p(i) квантиль.
Если X массив размерности d, затем Y массив с длиной самой маленькой операционной размерности, равной количеству квантилей, которые требуют (N или length(p)).
Многомерный массив является массивом больше чем с двумя размерностями. Например, если X 1 массивом 3 на 4, затем X трехмерный массив.
Неодноэлементная размерность массива является размерностью, размер которой не равен 1. Первая неодноэлементная размерность массива является первой размерностью, которая удовлетворяет неодноэлементному условию. Например, если X 1 1 2 4 массивами, затем третья размерность является первой неодноэлементной размерностью X.
Линейная интерполяция использует линейные полиномы, чтобы найти yi = f (xi), значения базового функционального Y = f (X) в точках в векторе или массиве x. Учитывая точки данных (x 1, y 1) и (x 2, y 2), где y 1 = f (x 1) и y 2 = f (x 2), линейная интерполяция находит y = f (x) для данного x между x 1 и x 2 можно следующим образом:
Точно так же, если 1.5/n квантилем является y 1.5/n, и 2.5/n квантилем является y 2.5/n, то линейная интерполяция находит 2.3/n квантиль y 2.3/n как
T-обзор [2] является вероятностной структурой данных, которая является разреженным представлением эмпирической кумулятивной функции распределения (CDF) набора данных. T-обзор полезен для вычислительных приближений основанной на ранге статистики (таких как процентили и квантили) из онлайновых или распределенных данных способом, которые допускают управляемую точность, особенно около хвостов распределения данных.
Для данных, которые распределяются в различных разделах, t-обзор вычисляет оценки квантиля (и оценки процентили) для каждого раздела данных отдельно, и затем комбинирует оценки при поддержании постоянной памяти связанная и постоянная относительная точность расчета ( для q th квантиль). По этим причинам t-обзор практичен для работы с длинными массивами.
Чтобы оценить квантили, массив, который распределяется в различных разделах, сначала создайте t-обзор в каждом разделе данных. T-обзор кластеризирует данные в разделе и обобщает каждый кластер центроидным значением и накопленным весом, который представляет количество выборок, способствующих кластеру. T-обзор использует большие кластеры (широко расставленные центроиды), чтобы представлять области CDF, которые являются около q = 0.5 и использует небольшие кластеры (плотно распределенные центроиды), чтобы представлять области CDF, которые являются около q = 0 или q = 1.
T-обзор управляет размером кластера при помощи масштабирующейся функции, которая сопоставляет квантиль q с индексом k параметром сжатия . Таким образом,
где отображение k является монотонным с минимальным значением k (0, δ) = 0 и максимальное значение k (1, δ) = δ. Следующий рисунок показывает масштабирующуюся функцию для δ = 10.
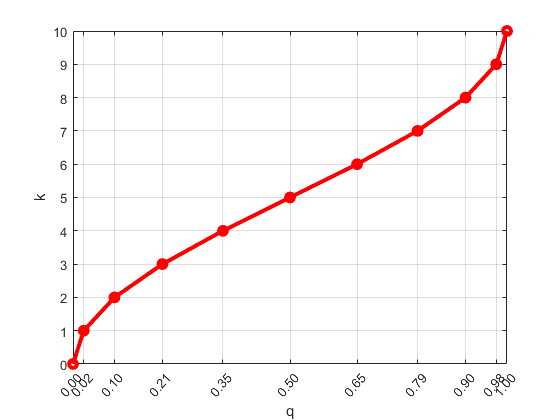
Масштабирующаяся функция переводит квантиль q в масштабный коэффициент k для того, чтобы дать переменные шаги размера в q. В результате размеры кластера неравны (больше вокруг центральных квантилей и меньший около q = 0 или q = 1). Меньшие кластеры допускают лучшую точность около ребер данных.
Чтобы обновить t-обзор с новым наблюдением, которое имеет вес и местоположение, найдите кластер самым близким к новому наблюдению. Затем добавьте вес и обновите центроид кластера на основе взвешенного среднего, при условии, что обновленный вес кластера не превышает ограничение размера.
Можно объединить независимые t-обзоры от каждого раздела данных путем взятия объединения t-обзоров и слияния их центроидов. Объединить t-обзоры, первый вид кластеры из всех независимых t-обзоров в порядке убывания кластерных весов. Затем объедините соседние кластеры, когда они будут соответствовать ограничению размера, чтобы сформировать новый t-обзор.
Если вы формируете t-обзор, который представляет набор полных данных, можно оценить конечные точки (или контуры) каждого кластера в t-обзоре и затем использовать интерполяцию между конечными точками каждого кластера, чтобы найти точные оценки квантиля.
Для n - вектор элемента X, quantile вычисляет квантили при помощи основанного на сортировке алгоритма можно следующим образом:
Отсортированные элементы в X взяты в качестве (0.5/n), (1.5/n)..., ([n – 0.5]/n) квантили. Например:
Для вектора данных пяти элементов такой как {6, 3, 2, 10, 1}, отсортированные элементы {1, 2, 3, 6, 10} соответственно соответствуют 0.1, 0.3, 0.5, 0.7, 0,9 квантиля.
Для вектора данных шести элементов такой как {6, 3, 2, 10, 8, 1}, отсортированные элементы {1, 2, 3, 6, 8, 10} соответственно соответствуют (0.5/6), (1.5/6), (2.5/6), (3.5/6), (4.5/6), (5.5/6) квантили.
quantile Линейная интерполяция использования, чтобы вычислить квантили для вероятностей между (0.5/n) и ([n – 0.5]/n).
Для квантилей, соответствующих вероятностям вне той области значений, quantile присваивает минимальные или максимальные значения элементов в X.
quantile обработки NaNs как отсутствующие значения и удаляет их.
[1] Лэнгфорд, E. “Квартили в элементарной статистике”, журнал образования статистики. Издание 14, № 3, 2006.
[2] Причинение беспокойства, T. и О. Эртл. “Вычисляя чрезвычайно Точные квантили Используя T-обзоры”. Август 2017.
Указания и ограничения по применению:
Y = quantile(X,p) и Y = quantile(X,N) возвратите точные квантили (использующий основанный на сортировке алгоритм) только если X высокий вектор-столбец.
Y = quantile(__,dim) возвращает точные квантили только, когда одно из этих условий существует:
X высокий вектор-столбец.
X длинный массив и dim не 1. Например, quantile(X,p,2) возвращает точные квантили вдоль строк длинного массива X.
Если X длинный массив и dim 1, затем необходимо задать 'Method','approximate' использовать алгоритм аппроксимации на основе T-обзора для вычисления квантилей. Например, quantile(X,p,1,'Method','approximate') возвращает аппроксимированные квантили вдоль столбцов длинного массива X.
Y = quantile(__,vecdim) возвращает точные квантили только, когда одно из этих условий существует:
X высокий вектор-столбец.
X длинный массив и vecdim не включает 1. Например, если X 3 5 2 массивами, затем quantile(X,p,[2,3]) возвращает точные квантили элементов в каждом X(i,:,:) срез.
X длинный массив и vecdim включает 1 и все неодноэлементные размерности X. Например, если X 10 массивом 1 на 4, затем quantile(X,p,[1 3]) возвращает точные квантили элементов в X(:,1,:).
Если X длинный массив и vecdim включает 1 но не включает все неодноэлементные размерности X, затем необходимо задать 'Method','approximate' использовать алгоритм аппроксимации. Например, если X 10 массивом 1 на 4, можно использовать quantile(X,p,[1 2],'Method','approximate') найти аппроксимированные квантили каждой страницы X.
Для получения дополнительной информации смотрите Длинные массивы (MATLAB).
Указания и ограничения по применению:
'all' и vecdim входные параметры не поддержаны.
'Method' аргумент пары "имя-значение" не поддержан.
dim входной параметр должен быть постоянным временем компиляции.
Если вы не задаете dim входной параметр, работа (или работа) размерность может отличаться в сгенерированном коде. В результате ошибки времени выполнения могут произойти. Для получения дополнительной информации смотрите Автоматическое ограничение размерности (MATLAB Coder).
Если выход Y вектор, ориентация Y отличается от MATLAB®, когда все следующее верно:
Вы не предоставляете dim.
X массив переменного размера, и не вектор переменного размера, во время компиляции, но X вектор во время выполнения.
Ориентация векторного X не совпадает с ориентацией векторного p.
В этом случае, выход Y совпадает с ориентацией X, не ориентация p.
Для получения дополнительной информации о генерации кода смотрите Введение в Генерацию кода и Общий Рабочий процесс Генерации кода.
Указания и ограничения по применению:
'all' и vecdim входные параметры не поддержаны.
'Method' аргумент пары "имя-значение" не поддержан.
Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.