И обратные преобразования Фурье Фурье

Эта страница показывает рабочий процесс для и обратных преобразований Фурье Фурье в Symbolic Math Toolbox™. Для простых примеров смотрите fourier и ifourier. Здесь, рабочий процесс для преобразований Фурье продемонстрирован путем вычисления отклонения луча из-за силы. Связанное дифференциальное уравнение решено преобразованием Фурье.

Определение преобразования Фурье

Преобразование Фурье f (x) относительно x в w

$F (w) = \int_{- \infty}^{\infty} f (x) e^{- i w x} d x .$

Обратное преобразование Фурье

$f (x) = \frac{1}{2 π} \int_{- \infty}^{\infty} F (w) e^{i w x} d w .$

Концепция: Используя символьные рабочие процессы

Символьные рабочие процессы сохраняют вычисления в естественной символьной форме вместо числовой формы. Этот подход помогает вам изучить свойства своего решения и использовать точные символьные значения. Вы заменяете числами вместо символьных переменных только, когда вы требуете числового результата, или вы не можете продолжить символически. Для получения дополнительной информации смотрите, Выбирают Symbolic or Numeric Arithmetic. Как правило, шаги:

Объявите уравнения.
Решите уравнения.
Замените значениями.
Постройте результаты.
Анализ результатов.

Вычислите отклонение луча Используя преобразование Фурье

Определите уравнения

Преобразование Фурье может использоваться, чтобы решить обыкновенные дифференциальные уравнения и дифференциальные уравнения с частными производными. Например, можно смоделировать отклонение бесконечно долгой опоры луча на эластичную основу под силой точки. Соответствующим реальным примером являются железнодорожные пути на основе. Железнодорожные пути являются бесконечно длинным лучом, в то время как основа эластична.

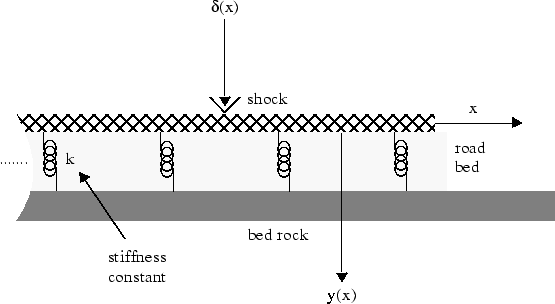
Пусть

E быть эластичностью луча (или железнодорожный путь).
I быть вторым моментом области поперечного сечения луча.
k быть пружинной жесткостью основы.

Дифференциальное уравнение

$\frac{d^{4} y}{d x^{4}} + \frac{k}{E I} y = \frac{1}{E I} δ (x), - \infty < x < \infty .$

Задайте функциональный y(x) и переменные. Примите Ei, и k положительны.

syms Y(x) w E I k f
assume([E I k] > 0)

Присвойте модули переменным при помощи symunit.

u = symunit;
Eu = E*u.Pa;    % Pascal
Iu = I*u.m^4;   % meter^4
ku = k*u.N/u.m^2;  % Newton/meter^2
X = x*u.m;
F = f*u.N/u.m;

Определите дифференциальное уравнение.

eqn = diff(Y,X,4) + ku/(Eu*Iu)*Y == F/(Eu*Iu)

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) == ...
            (f/(E*I))*([N]/([Pa]*[m]^5))

Представляйте силу f Дираком дельта функционируют δ (x).

eqn = subs(eqn,f,dirac(x))

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) ==...
           (dirac(x)/(E*I))*([N]/([Pa]*[m]^5))

Решите уравнения

Вычислите преобразование Фурье eqn при помощи fourier с обеих сторон eqn. Преобразование Фурье преобразует дифференцирование в экспоненты w.

eqnFT = fourier(lhs(eqn)) == fourier(rhs(eqn))

eqnFT =
w^4*fourier(Y(x), x, w)*(1/[m]^4) + ((k*fourier(Y(x), x, w))/(E*I))*([N]/([Pa]*[m]^6)) == (1/(E*I))*([N]/([Pa]*[m]^5))

Изолированный fourier(Y(x),x,w) в уравнении.

eqnFT = isolate(eqnFT, fourier(Y(x),x,w))

eqnFT =
fourier(Y(x), x, w) == (1/(E*I*w^4*[Pa]*[m]^2 + k*[N]))*[N]*[m]

Вычислите Y(x) путем вычисления обратного преобразования Фурье правой стороны. Упростите результат.

YSol = ifourier(rhs(eqnFT));
YSol = simplify(YSol)

YSol =
((exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) +...
 pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4)))*[m]

Проверяйте тот YSol имеет правильные размерности путем замены YSol в eqn и использование checkUnits функция. checkUnits возвращает логический 1 TRUE), значение eqn теперь имеет совместимые модули тех же физических размерностей.

checkUnits(subs(eqn,Y,YSol))

ans = 
  struct with fields:

    Consistent: 1
    Compatible: 1

Разделите выражение от модулей при помощи separateUnits.

YSol = separateUnits(YSol)

YSol =
(exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) + pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4))

Замените значениями

Используйте значения E = ^{106 Па}, I = ^{10-3 m4} и k = ¹⁰⁶ ^N/m2. Замените этими значениями в YSol и преобразуйте в плавающую точку при помощи vpa с 16 цифрами точности.

values = [1e6 1e-3 1e5];
YSol = subs(YSol,[E I k],values);
YSol = vpa(YSol,16)

YSol =
0.0000158113883008419*exp(-2.23606797749979*abs(x))*sin(2.23606797749979*abs(x) + 0.7853981633974483)

Постройте результаты

Постройте результат при помощи fplot.

fplot(YSol)
xlabel('x')
ylabel('Deflection y(x)')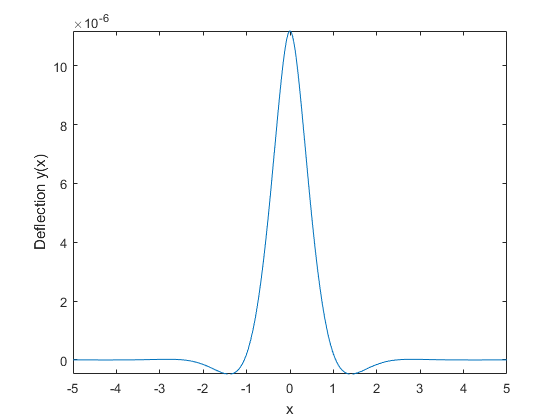

Анализ результатов

График показывает, что отклонение луча из-за силы точки высоко локализуется. Отклонение является самым большим при ударе и затем уменьшается быстро. Символьный результат позволяет вам анализировать свойства результата, который не возможен с числовыми результатами.

Заметьте тот YSol продукт условий. Термин с sin показывает, что ответ вибрирует колебательное поведение. Термин с exp показывает, что колебательное поведение быстро ослабляется экспоненциальным затуханием как расстояние от увеличений точки падений ракет.

Документация