Функция дельты Дирака
Вычислите производные и интегралы выражений, включающих дельту Дирака и функции Heaviside.
Найдите первые и вторые производные функции Heaviside. Результатом является функция дельты Дирака и ее первая производная.
syms x diff(heaviside(x), x) diff(heaviside(x), x, x)
ans = dirac(x) ans = dirac(1, x)
Найдите неопределенный интеграл функции дельты Дирака. Результаты возвращены int не включайте константы интегрирования.
int(dirac(x), x)
ans = sign(x)/2
Найдите интеграл этого выражения, включающего функцию дельты Дирака.
syms a int(dirac(x - a)*sin(x), x, -Inf, Inf)
ans = sin(a)
dirac учитывает предположения на переменных.
syms x real assumeAlso(x ~= 0) dirac(x)
ans = 0
Для дальнейших расчетов очистите предположения на x путем воссоздания его с помощью syms.
syms x
Вычислите функцию дельты Дирака x и его первые три производные.
Используйте векторный n = [0, 1, 2, 3] задавать порядок производных. dirac функция расширяет скаляр в вектор одного размера с n и вычисляет результат.
n = [0, 1, 2, 3]; d = dirac(n, x)
d = [ dirac(x), dirac(1, x), dirac(2, x), dirac(3, x)]
Замените x с 0.
subs(d, x, 0)
ans = [ Inf, -Inf, Inf, -Inf]
Чтобы обработать бесконечность в 0, используйте числовые значения вместо символьных значений. Продолжите строить все другие символьные входные параметры символически при помощи fplot.
Установите Inf значение к 1 и постройте при помощи stem.
x = -1:0.1:1; y = dirac(x); idx = y == Inf; % find Inf y(idx) = 1; % set Inf to finite value stem(x,y)
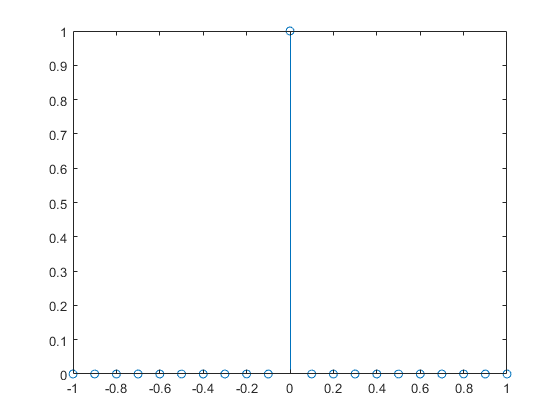
Для комплексных чисел x с ненулевыми мнимыми частями, dirac возвращает NaN.
dirac возвращает результаты с плавающей точкой для числовых аргументов, которые не являются символьными объектами.
dirac действия, поэлементные на нескалярных входных параметрах.
По крайней мере один входной параметр должен быть скаляром, или оба аргумента должны быть векторами или матрицами, одного размера. Если один входной параметр является скаляром, и другой является вектором или матрицей, то dirac расширяет скаляр в вектор или матрицу одного размера с другим аргументом со всеми элементами, равными тому скаляру.