export::stlЭкспортируйте данные о STL
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
export::stl(filename,[x, y, z],u = umin .. umax,v = vmin .. vmax,options) export::stl(n,[x, y, z],u = umin .. umax,v = vmin .. vmax,options) export::stl(filename,object1, <object2, …>,options) export::stl(n,object1, <object2, …>,options)
export::stl используется, чтобы создать триангуляцию параметрической поверхности и написать данные о триангуляции в формате STL к внешнему файлу.
Файлы STL содержат данные о триангуляции 3D поверхностей. Каждый треугольник хранится как нормальный модуль и три вершины. Нормальное и вершины заданы тремя координатами каждый, таким образом, существует в общей сложности 12 чисел, сохраненных для каждого треугольника. Считайте раздел “Background” этой страницы справки для получения дальнейшей информации.
Если поверхность закрывается, она рассматривается как контур 3D тела. Нормали треугольников, записанных в файл STL, должны указать с внутренней части тела к внешней стороне.
Обратите внимание на то, что направление нормалей, что export::stl записи в файл STL зависят от параметризации x (u, v), y (u, v), z (u, v)!
Если p1 = (x(u, v), y(u, v), z(u, v)), p2 = (x(u + du, v), y(u + du, v), z(u + du, v)), p3 = (x(u, v + dv), y(u, v + dv), z(u, v + dv)) углы треугольника, нормальным, сопоставленным с этим треугольником, является векторное произведение стороны p2 - p1 времена сторона p3 - p2. Стандартный export::stl выбирает соседние значения поверхностных параметров с du = (`u_{max}` - `u_{min}`)/(n_u - 1) и dv = (`v_{max}` - `v_{min}`)/(n_v - 1), соответственно.
Таким образом, если ваша параметризация такова что векторное произведение векторов p2 - p1 и p3 - p2 не указывает на за пределами вашего тела, только необходимо позволить одному из параметров (u, скажите), запуск от umax к umin вместо от umin к umax. Только замените свой вызов
export::stl(filename, [x,y,z], u = `u_{min}` .. `u_{max}`, v = `v_{min}` .. `v_{max}`)
export::stl(filename, [x,y,z], u = `u_{max}` .. `u_{min}`, v = `v_{min}` .. `v_{max}`).
До несоответствующего упорядоченного расположения в файле STL треугольники, сгенерированные этими вызовами, являются тем же самым кроме направления нормального, сопоставленного с каждым треугольником.
Если файл задан символьной строкой, соответствующий файл открыт и закрыт, автоматически.
Как альтернатива определению файла строкой, пользователь может открыть файл сам через fopen в Write режим и передача дескриптор файла, возвращенный fopen к export::stl. Если двоичные данные должны быть записаны в файл, убедитесь, что он открыт с Raw, т.е. вызовите fopen(filename, Write, Raw).
Обратите внимание на то, что export::stl не закрывает файл автоматически, если он задан дескриптором файла. Это остается открытым после export::stl закончил его задание. Файл должен быть закрыт явным образом пользователем, использующим fclose.
Если файл задан символьной строкой, имя может соответствовать абсолюту или относительному пути. В частности, переменная окружения WRITEPATH учтен. Детали о странице справки fopen содержите для export::stl, также.
С опцией Append, файл сначала открыт для чтения и, после чтения данных в файле, открылся для записи. Если никакой абсолютный путь не используется, чтобы задать файл, убедитесь что переменные окружения READPATH и WRITEPATH укажите на ту же папку. В качестве альтернативы это - хорошая идея поместить файл в ту же папку как блокнот MuPAD®, который вы в настоящее время используете. Если этот блокнот сохранен на диске вашего компьютера, абсолютный путь доступен как переменная окружения NOTEBOOKPATH. Таким образом, задавая файл с именем “myfile.stl”, скажем, абсолютным путем NOTEBOOKPATH."myfile.stl" гарантирует, что файл найден в той же папке как ваш блокнот.
Текстовые файлы сгенерировали с опцией Text или эквивалентный Ascii может быть открыт и считан с любым текстовым редактором. Однако двоичные файлы сгенерировали с опцией Bin или эквивалентные опции Binary или Raw быстрее, чтобы создать и обработать.
Файл сгенерирован export::stl может читаться и визуализироваться в MuPAD с помощью графика примитивный plot::SurfaceSTL.
Если имя файла, данное концы в “.gz”, export::stl записывает сжатый файл, который может быть считан любой программой, поддерживающей gzip сжатие.
Функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность. Текущее значение DIGITS определяет количество значительных десятичных цифр, с которыми данные о STL записаны в заданный файл. (Это содержит для текстовых файлов. В бинарных файлах STL все численные значения имеют точность приблизительно 7 десятичных цифр.) Для внутреннего расчета данных MuPAD, значением DIGITS временно увеличен на 10, чтобы минимизировать эффекты округления.
Данные о STL сгенерированы export::stl записаны в заданный файл.
Мы генерируем сферу, данную следующей параметризацией:
x:= cos(u)*sin(v): y:= sin(u)*sin(v): z:= cos(v):
Мы вызываем export::stl сгенерировать данные о STL и записать им в файл с именем “sphere.stl”. Файл должен быть сгенерирован в той же директории как текущий блокнот MuPAD, который мы используем. Следовательно, мы задаем абсолютный путь для файла с помощью пути текущего блокнота. Если этот блокнот был сохранен в диск вашего компьютера, этот путь доступен в переменной окружения NOTEBOOKPATH:
filename:= NOTEBOOKPATH."sphere.stl": export::stl(filename, [x, y, z], u = 0 .. 2*PI, v = 0 .. PI, Text)
Поскольку файл был создан в Text формат, это может быть открыто с любым текстовым редактором. Это должно выглядеть так:
solid MuPADtoSTL1 facet normal -0.06540070486 -0.008610166138 -0.9978219344 outer loop vertex 100.0 100.0 300.0 vertex 112.607862 103.3782664 298.7167292 vertex 113.0526192 100.0 298.7167292 endloop endfacet facet normal -0.1950260058 -0.02567566076 -0.9804619409 outer loop vertex 113.0526192 100.0 298.7167292 vertex 112.607862 103.3782664 298.7167292 vertex 125.0 106.6987298 294.8888739 endloop endfacet ... endsolid MuPADtoSTL1
Мы повторно импортируем данные о STL и визуализируем поверхность с помощью plot::SurfaceSTL:
plot(plot::SurfaceSTL(filename, MeshVisible))
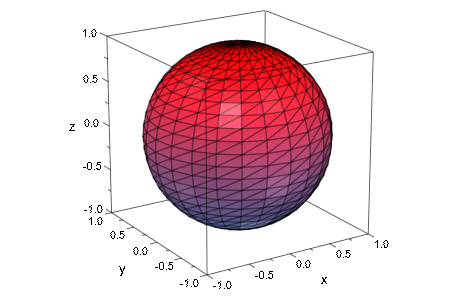
Мы сокращаем количество значительных выходных цифр к разумному размеру. Далее, мы задаем размер mesh и запрашиваем определенное окно для вывода:
DIGITS:= 7:
export::stl(filename, [x, y, z], u = 0..2*PI, v = 0..PI,
Mesh = [10, 10],
OutputBox = [-100..100, -100..100, -100..100],
Text):Файл теперь должен выглядеть так:
solid MuPADtoSTL2 facet normal -0.1733024 -0.06307691 -0.9828467 outer loop vertex -3.10912 0.000000002143114 100.0 vertex 24.32249 22.66816 93.96926 vertex 32.7003 0.000000002143114 93.96926 endloop endfacet ... endsolid MuPADtoSTL2
Мы визуализируем новое содержимое файла:
plot(plot::SurfaceSTL(filename, MeshVisible))
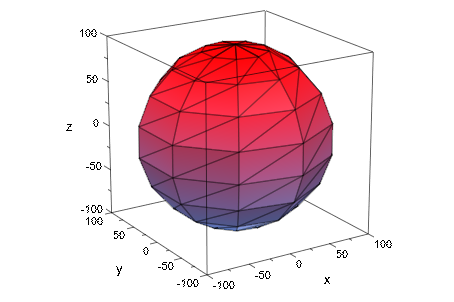
delete x, y, z, filename, DIGITS:
Мы задаем параметризацию поверхности смесью выражений и процедур:
x:= piecewise([0.1 < u < 0.9, u*cos(v)], [Otherwise, 0]):
y:= (u, v) -> piecewise([0.1 < u < 0.9, u*sin(v)], [Otherwise, 0]):
z:= (u, v) -> if u <= 0.1 then exp(-0.1)
elif u < 0.9 then exp(-u)
else exp(-0.9)
end_if:Это - поверхность, которую мы хотим экспортировать в STL:
plot(plot::Surface([x, y, z], u = 0..1, v = 0..2*PI,
Mesh = [100, 36])):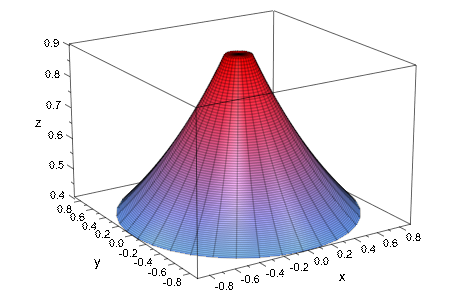
Мы принимаем, что нет никакого внешнего файла “sample.stl”. Мы создаем его путем открытия его в Write режим в той же директории как текущий блокнот MuPAD, который мы используем. Следовательно, мы задаем абсолютный путь для файла с помощью пути текущего блокнота. Если этот блокнот был сохранен в дисковод вашего компьютера, этот путь доступен в переменной окружения NOTEBOOKPATH. Дескриптор файла n возвращенный fopen передается export::stl:
filename:= NOTEBOOKPATH."sample.stl":
DIGITS:= 7:
export::stl(filename, [x, y, z], u = 0..1, v = 0..2*PI,
Mesh = [30, 36])Мы повторно импортируем данные о STL и визуализируем поверхность с помощью plot::SurfaceSTL:
plot(plot::SurfaceSTL(filename, MeshVisible))
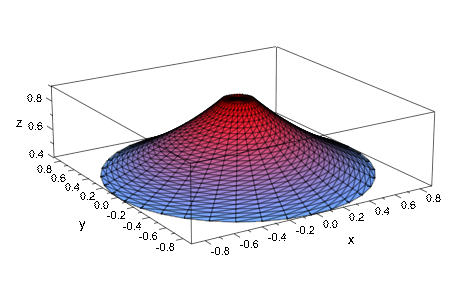
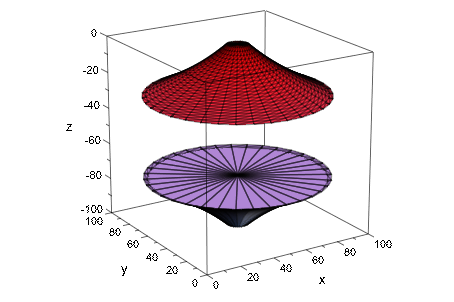
Мы можем добавить дальнейшую поверхность к файлу с помощью опции Append:
export::stl(filename, [x, y, -z], u = 0..1, v = 0..2*PI,
Mesh = [30, 36],
OutputBox = [0..100, 0..100, -100..0],
Append)Мы визуализируем новое содержимое файла через plot::SurfaceSTL:
plot(plot::SurfaceSTL(filename, MeshVisible))
delete x, y, z, filename, DIGITS:
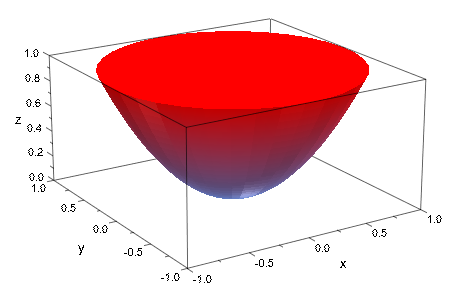
Мы хотим создать закрытую поверхность, состоящую из “миски” с “крышкой”.
bowl:= [u*cos(v), u*sin(v), u^2], u = 0 .. 1, v = 0 .. 2*PI: lid:= [u*cos(v), u*sin(v), 1 ], u = 0 .. 1, v = 0 .. 2*PI:
filename:= NOTEBOOKPATH."sample.stl": DIGITS:= 7: export::stl(filename, bowl, Mesh = [30, 36]): export::stl(filename, lid, Mesh = [30, 36], Append): plot(plot::SurfaceSTL(filename), Scaling = Constrained):
delete filename, DIGITS:
Мы демонстрируем опции Scaling = Constrained и Scaling = Unconstrained. С Scaling = Constrained, координаты, данные параметризацией x, y, z масштабируются тем же фактором, чтобы вместить поверхность в окно для вывода. Здесь, мы создаем сферу радиуса 1. Окно для вывода не является кубом: область значений для z координата особенно больше, чем для x и y. Тем не менее, сфера остается сфера при использовании Scaling = Constrained. Однако окно для вывода не абсолютно заполнено сферой:
x:= cos(u)*sin(v):
y:= sin(u)*sin(v):
z:= cos(v):
DIGITS:= 7:
filename:= NOTEBOOKPATH."sphere.stl":
export::stl(filename, [x, y, z], u = 0 .. 2*PI, v = 0 .. PI,
OutputBox = [-1 .. 1, -1 .. 1, -3 .. 3],
Scaling = Constrained):
plot(plot::SurfaceSTL(filename,
Scaling = Constrained,
MeshVisible))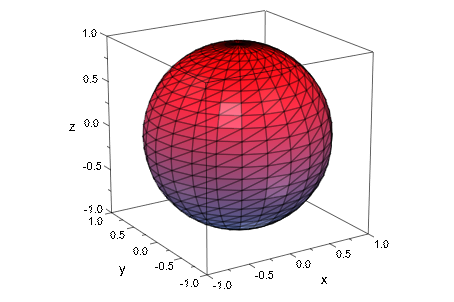
С Scaling = Unconstrained, сфера деформирована к эллипсоиду, заполняющему окно для вывода:
export::stl(filename, [x, y, z], u = 0..2*PI, v = 0..PI,
OutputBox = [-1..1, -1..1, -3..3],
Scaling = Unconstrained):
plot(plot::SurfaceSTL(filename,
Scaling = Constrained,
MeshVisible))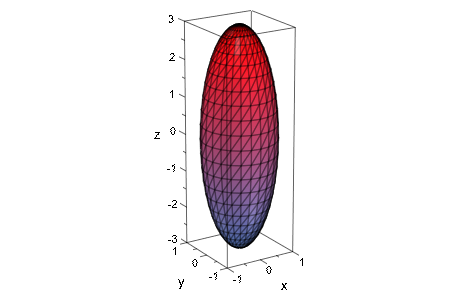
delete x, y, z, filename, DIGITS:
| |
|
Дескриптор файла обеспечивается |
|
3D графические объекты |
|
Координатные функции: арифметические выражения или |
|
Первый поверхностный параметр: идентификатор или индексируемый идентификатор. |
|
Область значений для параметра u: |
|
Второй поверхностный параметр: идентификатор или индексируемый идентификатор. |
|
Область значений для параметра v: |
|
Опция, заданная как Наборы размер mesh: целочисленный |
|
Опция, заданная как По умолчанию координаты точек mesh, задающих объект STL, записаны в файл в соответствии с параметризацией поверхности. Таким образом, если несколько объектов записаны в файл с помощью опции Опция ПримечаниеЕсли несколько объектов записаны в файл с помощью опции Эта последняя возможность переключает и масштабирует все координаты всех поверхностей в файле, таким образом, что целая сцена объектов помещается в окно для вывода. Относительный размер и положения объектов сохраняются. Смотрите пример 3. Эта опция является довольно дорогой, поскольку все данные в файле STL должны быть изменены! Эта опция не доступна, если файл был открыт вне |
|
Опция, заданная как С С Эта опция проигнорирована если не используемый в сочетании с |
|
С синонимичными флагами |
|
С этим флагом данные о STL поверхности добавлены в существующий файл с именем STL “имя файла”. Если никакой такой файл не существует, это создается и обрабатывается как без |
null() объект.
Существует два формата устройства хранения данных, доступные для файлов STL, которые являются ASCII и ДВОИЧНЫМ ФАЙЛОМ. ASCII-файлы человекочитаемы, в то время как Двоичные файлы меньше и быстрее к процессу. Оба ASCII, а также Двоичные файлы могут быть сгенерированы export::stl. Типичный файл STL ASCII выглядит так:
solid sample
facet normal -4.470293E-02 7.003503E-01 -7.123981E-01
outer loop
vertex -2.812284E+00 2.298693E+01 0.000000E+00
vertex -2.812284E+00 2.296699E+01 -1.960784E-02
vertex -3.124760E+00 2.296699E+01 0.000000E+00
endloop
endfacet
...
endsolid sample
Двоичные файлы STL имеют следующий формат:
Bytes Type Description
80 ASCII header, no data significance
4 uint number of facets in file
4 float normal x - start of facet
4 float normal y
4 float normal z
4 float vertex1 x
4 float vertex1 y
4 float vertex1 z
4 float vertex2 x
4 float vertex2 y
4 float vertex2 z
4 float vertex3 x
4 float vertex3 y
4 float vertex3 z
2 byte not used - end of facet
...
Фасетная ориентация: фасеты задают поверхность 3D объекта. По сути, каждый фасет является частью контура между внутренней частью и внешним видом объекта. Ориентация фасетов (какой путь отсутствует и в котором находится путь) задана избыточно двумя способами, которые должны быть сопоставимыми. Во-первых, направление нормального является исходящим. Во-вторых, который обычно используется в наше время, фасетные вершины перечислены в против часовой стрелки порядке при рассмотрении объекта от внешнего (правило правой руки).
Правило от вершины к вершине: Каждый треугольник должен совместно использовать две вершины с каждым из его смежных треугольников. Другими словами, вершина одного треугольника не может лечь на сторону другого.
Оси: формат указывает, что все координаты вершины должны быть строго положительными числами. Однако кажется, что – за немногим исключением – большая часть программного обеспечения, используемого сегодня (включенный MuPAD), позволяет отрицательные координаты также.
Модули: файл STL не содержит информации о шкале; координаты могут быть интерпретированы в произвольных модулях.
Более подробная информация о формате файла STL доступна в сети, например, в:
www.ennex.com/fabbers/StL.asp,
www.math.iastate.edu/burkardt/data/stl/stl.html и
rpdrc.ic.polyu.edu.hk/content/stl/stl_introduction.htm.
Наборы файлов примера STL могут быть найдены в сети, например, в:
www.wohlersassociates.com/Software-for-Rapid-Prototyping.html и
www.cs.duke.edu / ~ edels/Tubes.
Информация о технологиях быстрого прототипирования доступна в сети, например, в:
www.cs.hut.fi / ~ ado/rp/rp.html.