numeric::rationalizeАппроксимируйте число с плавающей запятой рациональным числом
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numeric::rationalize(object, <Exact | Minimize | Restore>, <digits>)
numeric::rationalize(object) замены все числа с плавающей запятой в object рациональными числами.
Объект области библиотеки, охарактеризованной domtype(extop(object,0))=DOM_DOMAIN возвращен неизменный. Для всех других объектов, numeric::rationalize применяется рекурсивно ко всем операндам. Объекты областей библиотеки могут быть рационализированы, если область имеет соответствующий map метод. Смотрите Пример 5.
Число с плавающей запятой f аппроксимировано рациональным числом r, удовлетворяющий |f - r | <ε | f |.
С опциями Exact и Minimize, гарантируемая точность![]() . С
. С Restore, гарантируемая точность только![]() .
.
Точностью по умолчанию является digits = DIGITS.
Определяемая пользователем точность не должна быть больше, чем внутренняя точность с плавающей точкой, установленная DIGITS: ошибка происходит для digits > DIGITS.
Функция чувствительна к переменной окружения DIGITS.
numeric::rationalize применяется к каждому операнду составного объекта:
numeric::rationalize(0.2*a+b^(0.7*I))
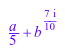
numeric::rationalize([{poly(0.2*x, [x]), sin(7.2*PI) + 1.0*I},
exp(3 + ln(2.0*x))])![]()
Мы демонстрируем стратегию по умолчанию Exact:
numeric::rationalize(12.3 + 0.5*I), numeric::rationalize(0.33333), numeric::rationalize(1/3.0)
![]()
numeric::rationalize(10^12/13.0), numeric::rationalize(10^(-12)/13.0)
![]()
Мы уменьшаем точность приближения к 5 цифрам:
numeric::rationalize(10^12/13.0, 5), numeric::rationalize(10^(-12)/13.0, 5)
![]()
Мы демонстрируем стратегию Minimize для минимизации сложности получившегося рационального числа:
numeric::rationalize(1/13.0, 5), numeric::rationalize(1/13.0, Minimize, 5), numeric::rationalize(0.333331, 5), numeric::rationalize(0.333331, Minimize, 5), numeric::rationalize(14.285, 5), numeric::rationalize(14.2857, Minimize, 5), numeric::rationalize(1234.1/56789.2), numeric::rationalize(1234.1/56789.2, Minimize)
![]()
Мы вычисляем рациональные приближения π с различной точностью:
numeric::rationalize(float(PI), Minimize, i) $ i = 1..10
![]()
Мы демонстрируем стратегию Restore для восстановления рациональных чисел после элементарных операций плавающих. Во многих случаях, также Minimize восстановления стратегии:
numeric::rationalize(1/7.3, Exact), numeric::rationalize(1/7.3, Minimize), numeric::rationalize(1/7.3, Restore)
![]()
Однако использование Restore улучшает возможности восстановления с эффектов округления:
numeric::rationalize(10^9/13.0, Minimize), numeric::rationalize(10^9/13.0, Restore)
![]()
DIGITS:= 11: numeric::rationalize(1234.56/12345.67, Minimize), numeric::rationalize(1234.56/12345.67, Restore)
![]()
В некоторых случаях, Restore умеет восстановиться с распространения ошибки округления в составных арифметических операциях:
DIGITS:= 10: x:= float(122393/75025): y:= float(121393/75025): z := (x^2 - y^2)/(x + y)
![]()
numeric::rationalize(z, Restore)
![]()
Результат с Restore соответствует точной арифметике:
rx := numeric::rationalize(x, Restore): ry := numeric::rationalize(y, Restore): rx, ry, (rx^2 - ry^2)/(rx + ry)
![]()
Обратите внимание на то, что приближение с Restore может иметь уменьшаемую точность только digits/2:
x := 1.0 + 1/10^6: numeric::rationalize(x, Exact), numeric::rationalize(x, Restore)
![]()
delete x, y, z, rx, ry:
Плавания в объектах областей библиотеки не рационализированы непосредственно. Однако для большинства областей соответствующий map метод может передать numeric::rationalize к операндам:
Dom::Multiset(0.2, 0.2, 1/5, 0.3)
![]()
numeric::rationalize(%), map(%, numeric::rationalize, Restore)
![]()
|
Произвольный объект MuPAD® |
|
Положительное целое число (количество десятичных цифр) не больше, чем переменная окружения |
|
Задает стратегию аппроксимации чисел с плавающей запятой рациональными числами. Это - стратегия по умолчанию, таким образом, нет никакой действительной потребности передать Любое действительное число с плавающей запятой f ≠ 0.0 имеет уникальное представление
С целочисленной экспонентой и 1,0 ≤ mantissa <10.0. С опцией
Это гарантирует относительную точность |
|
Задает стратегию аппроксимации чисел с плавающей запятой рациональными числами. Эта стратегия пытается минимизировать сложность рационального приближения, т.е. числители и знаменатели быть малыми. Гарантируемой точностью рационального приближения является Смотрите пример 3. |
|
Задает стратегию аппроксимации чисел с плавающей запятой рациональными числами. Эта стратегия пытается восстановить рациональные числа, полученные после того, как элементарные арифметические операции применились к числам с плавающей запятой. Например, для рационального ПримечаниеГарантируемой точностью рационального приближения является только Смотрите пример 4. |
Если аргумент является объектом некоторой области ядра, то это возвращено со всеми операндами с плавающей точкой, замененными рациональными числами. Объект некоторой области библиотеки возвращен неизменный.
object
Расширение непрерывной дроби (CF) используется с опциями Minimize и Restore.
С Minimize, первое приближение CF, удовлетворяющее критерию точности, возвращено.
Restore остановки алгоритма, когда большие коэффициенты расширения CF найдены.