ode::dAlembertДаламберово сокращение линейного гомогенного обыкновенного дифференциального уравнения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
ode::dAlembert(Ly, y(x), v)
ode::dAlembert(Ly, y(x), v) возвращает уменьшаемое дифференциальное уравнение Ly использование метода сокращения Даламбера и функционального v. Если v решение Ly и u решение уменьшаемого дифференциального уравнения затем, v ∈ t u является другим решением Ly.
Рассмотрите следующее дифференциальное уравнение:
Ly := 2/x^3*y(x)-2/x^2*diff(y(x),x)+1/x*diff(y(x),x$2)+
diff(y(x),x$3)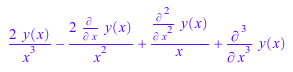
Мы легко проверяем тот x конкретное решение Ly:
ode::evalOde(Ly, y(x)=x)
Затем мы уменьшаем уравнение Ly использование этого специального решения:
R := ode::dAlembert(Ly, y(x), x)
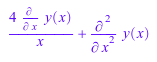
Решения уравнения R не слишком тверды, чтобы найти:
ode::evalOde(R, y(x)=1), ode::evalOde(R, y(x)=1/x^3)
Так основание решений Ly поэтому
, который может проверяться непосредственно:
ode::solve(Ly, y(x))
|
Гомогенное линейное дифференциальное уравнение. |
|
Зависимая функция |
|
Выражение. |
Выражение.