ode::isFuchsian
Тесты, если гомогенное линейное обыкновенное дифференциальное уравнение имеет тип Fuchsian
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
ode::isFuchsian(Ly, y(x), <AllExponents>)
Описание
ode::isFuchsian возвращает TRUE если Ly имеет тип Fuchsian, т.е. все особые точки (включая бесконечно удаленную точку) Ly являются регулярными. Это возвращает FALSE если по крайней мере одна особая точка неправильна. Когда опция AllExponents дан, любой FALSE возвращен или список, где каждый элемент является таблицей, содержащей в каждой регулярной особой точке Ly место, определяющее уравнение и экспоненты.
Примеры
Пример 1
Мы тестируем, если следующим дифференциальным уравнением является Fuchsian:
Ly:=x*(1-x)*diff(y(x),x$2)+(1-x)*diff(y(x),x)+10*y(x)
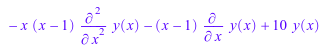
ode::isFuchsian(Ly, y(x))
Мы можем взглянуть определяющих уравнений, экспонент в каждой регулярной особой точке Ly:
ode::isFuchsian(Ly, y(x), AllExponents)
Пример 2
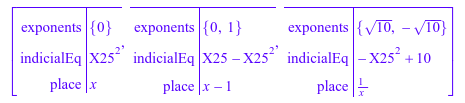
В этом примере, уравнении Эйри, единственная особая точка в бесконечности и неправильна:
ode::isFuchsian(diff(y(x),x$2)-x*y(x), y(x))
Параметры
|
Гомогенное линейное обыкновенное дифференциальное уравнение с коэффициентами в поле ℚ (x) рациональных функций по rationals. |
|
Зависимая функция |
Опции
|
Возвратите список таблиц indical уравнений и экспонент для регулярных особых точек. |