Взаимодействия среды

Функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.

Пример 1

Мы делим действительную линию на 4 интервала, которые равновероятны относительно стандартного нормального распределения:

k:= 4: q := stats::normalQuantile(0, 1):
cells := stats::equiprobableCells(k, q)

Мы проверяем кривую равных вероятностей путем применения функционального stats::normalCDF(0, 1) к границам ячейки:

cdf := stats::normalCDF(0, 1):
p := map(cells, map, cdf)

Вероятности ячейки даны различиями функции CDF, применился к границам ячейки:

(p[i][2] - p[i][1]) $ i = 1..k

Мы используем эти ячейки в тесте хи-квадрата для нормальности некоторых случайных данных:

r := stats::normalRandom(0, 1, Seed = 0):
data := [r() $ i = 1..1000]:
stats::csGOFT(data, cells, CDF = cdf)

С наблюдаемым уровнем значения данные проходят этот тест хорошо. Мы экспериментируем с другими равновероятными разделениями ячейки:

for k in [20, 30, 40, 50] do
    cells := stats::equiprobableCells(k, q);
    print(stats::csGOFT(data, cells, CDF = cdf));
end_for:

delete k, cells, p, cdf, r, data:

Пример 2

Мы создаем выборку 1 000 случайных целых чисел между 0 и 100:

SEED := 10^2: r := random(0 .. 100): 
data := [r() $ i = 1..1000]:

Мы создаем 'равновероятное' разделение ячейки 10 ячеек с помощью (дискретного) эмпирического распределения данных. Т.е. каждая из следующих ячеек должна содержать приблизительно то же количество данных из случайной выборки:

k := 10:
quantile := stats::empiricalQuantile(data):
cells := stats::equiprobableCells(k, quantile)

Для дискретных распределений 'кривая равных вероятностей' может только быть достигнута приблизительно. Мы вычисляем вероятности ячейки относительно эмпирической кумулятивной функции распределения (CDF) путем вычитания значения CDF левого контура от значения CDF правильного контура:

cdf := stats::empiricalCDF(data):
map(cells, cell -> cdf(cell[2]) - cdf(cell[1]))

Фактическая эмпирическая частота данных в каждой ячейке является временами вероятности ячейки объем выборки (1000):

map(cells, cell -> 1000*(cdf(cell[2]) - cdf(cell[1])))

При вычислении вероятности ячейки [b[i-1], b[i]] через cdf (b _i) - cdf (b _{i - 1}), ячейка рассматривается как полуоткрытый интервал математически. Поэтому точки данных 0 содержавшийся в выборке не считаются, и частоты ячейки действительно не совсем составляют в целом объем выборки:

_plus(op(%))

Для Символа:: тест chi^2, это не имеет значения, потому что он заменяет левый контур первой ячейки -infinity, так или иначе. С наблюдаемым уровнем значения данные проходят тест для равномерного распределения на уровнях настолько же высоко как:

stats::csGOFT(data, cells, CDF = stats::uniformCDF(0, 100))

Мы тестируем ли совпадение данных нормальное распределение с эмпирическим средним значением и отклонением:

[m, v] := [stats::mean(data), stats::variance(data)];
stats::csGOFT(data, cells, CDF = stats::normalCDF(m, v))

С наблюдаемым уровнем значения ясно должна быть отклонена гипотеза нормального распределения.

delete r, data, k, quantile, cells, cdf, m, v:

Пример 3

Мы считаем биномиальное распределение 'испытательным параметром' n = 100 и 'параметром вероятности'. Это - распределение количества успехов в n = 100 независимых Бернуллиевых экспериментов, каждый с вероятностью успеха. Эта случайная переменная может достигнуть дискретных значений 0, 1, …, 100. Мы создаем разделение ячейки 4 ячеек:

n := 100: p := 1/2:
quantile := stats::binomialQuantile(n, p):
cells := stats::equiprobableCells(4, quantile)

Из-за дискретности не существует точное равновероятное разделение ячейки. Мы вычисляем ожидаемые частоты ячейки таким же образом как в предыдущем примере:

cdf := stats::binomialCDF(n, p):
map(cells, cell -> n*(cdf(cell[2]) - cdf(cell[1])))

Мы создаем случайную выборку и применяем Символ:: тест chi^2:

r := stats::binomialRandom(n, p, Seed = 123):
data := [r() $ i = 1..100]:
stats::csGOFT(data, cells, CDF = cdf)

Наблюдаемый уровень значения не мал, т.е. данные проходят тест хорошо.

'Испытательный параметр' n = 100 является достаточно большим для биномиального распределения, которое будет аппроксимировано нормальным распределением со средним n  p и отклонение n  p   (1 - p). Данные проходят тест для нормального распределения, также:

cdf := stats::normalCDF(n*p, n*p*(1 - p)):
stats::csGOFT(data, cells, CDF = cdf)

Мы повторяем тест с другим разделением ячейки:

quantile :=  stats::normalQuantile(n*p, n*p*(1 - p)):
cells := stats::equiprobableCells(4, quantile)

stats::csGOFT(data, cells, CDF = cdf)

delete k, quantile, cells, cdf, r, data:

Пример 4

Мы демонстрируем пользовательские функции квантиля. Мы считаем следующее распределение случайной переменной X поддерживаемый на интервале [0, 1]:

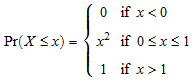
Функцией квантиля q дают для 0 ≤ x ≤ 1:

quantile := x -> sqrt(x):

Мы тестируем гипотезу, что следующие данные распределяются, как задано выше.

cells := stats::equiprobableCells(6, quantile)

data := [sqrt(frandom()) $ i = 1..10^3]:
cdf := proc(x)
       begin
         if x <= 0 then return(0)
         elif x <= 1 then return(x^2)
         else return(1)
         end_if
       end_proc:
stats::csGOFT(data, cells, CDF = cdf)

Данные проходят тест хорошо. На самом деле, для универсальной формы отклоняют Y на интервале [0, 1] (как произведено frandom), кумулятивная функция распределения действительно дана cdf.

delete quantile, cells, data, cdf:

Возвращаемые значения

Список k “ячейки”

со значениями с плавающей точкой. Это 'разделение ячейки' подходит как входной параметр для stats::csGOFT.