stats::csGOFTКлассический критерий согласия Хи-квадрат
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
stats::csGOFT(x1, x2, …,[[a1, b1], [a2, b2], …],CDF = f | PDF = f | PF = f) stats::csGOFT([x1, x2, …],[[a1, b1], [a2, b2], …],CDF = f | PDF = f | PF = f) stats::csGOFT(s, <c>,[[a1, b1], [a2, b2], …],CDF = f | PDF = f | PF = f)
stats::csGOFT(data, cells, CDF = f) применяет классический критерий согласия Хи-квадрат для нулевой гипотезы: “данные являются f-distributed”.
Критерий согласия Хи-квадрат делит действительную линию на интервалы k![]() ('ячейки'). Это вычисляет количество данных x j, попадающий в ячейки c i, и сравнивает эти 'эмпирические частоты ячейки' с 'ожидаемыми частотами ячейки' n pi, где n является объемом выборки и p i =, Pr (a i <x ≤ b i) является 'вероятностями ячейки' случайной переменной с предполагавшимся распределением, заданным
('ячейки'). Это вычисляет количество данных x j, попадающий в ячейки c i, и сравнивает эти 'эмпирические частоты ячейки' с 'ожидаемыми частотами ячейки' n pi, где n является объемом выборки и p i =, Pr (a i <x ≤ b i) является 'вероятностями ячейки' случайной переменной с предполагавшимся распределением, заданным X = f.
Все данные x1x2 и т.д. должно быть конвертируемым к действительным числам с плавающей запятой. Данные не должны быть отсортированы на входе: stats::csGOFT автоматически преобразует данные в плавания и сортирует их внутренне.
Внешние статистические данные, сохраненные в ASCII-файле, могут быть импортированы в сеанс MuPAD® через import::readdata. В частности, смотрите Пример 1 из соответствующей страницы справки.
Конечные границы ячейки a i, b i должен быть конвертируемым к действительным числам с плавающей запятой, удовлетворяющим a 1 <b 1 ≤ a 2 <b 2 ≤ a 3 <…. Они задают полуоткрытый меж-Вальс![]() .
.
Когда предполагавшееся распределение f задано как кумулятивная функция распределения (CDF = f), левый контур первой ячейки и правильный контур последней ячейки проигнорированы. Они заменяются - ∞ и infinity, соответственно, т.е. разделение ячейки
![]()
используется внутренне.
Ячейки должны быть непересекающимися. Их объединение должно покрыть область поддержки распределения, т.е. 'вероятности ячейки' p i =, Pr (a i <x ≤ b i) должен составить в целом 1 для случайной переменной x с предполагавшимся распределением, данным f. Для непрерывных распределений, соседних элементов с b 1 = a 2, b 2 = a 3, … являются соответствующими.
Можно использовать a 1 = - ∞ и b k = ∞ для распределений, поддержанных на целой действительной линии.
Ячейки должны быть выбраны таким образом, что никакая вероятность ячейки p i не исчезает!
Смотрите раздел 'Background' этой страницы справки для рекомендаций на разделении ячейки. В частности, использование равновероятных ячеек (с постоянным p i) рекомендуется. Для удобства, служебная функция stats::equiprobableCells обеспечивается, чтобы сгенерировать такие ячейки. Смотрите Пример 1, Пример 3 и Пример 4.
Распределение, на которое тестируются данные, задано уравнением X = f, где X один из флагов CDF, PDF или PF.
Для КПД рекомендуется задать кумулятивную функцию распределения (CDF = f).
Функциональный f может быть процедура, предоставленная MuPAD stats библиотека. Спецификации, такие как CDF = stats::normalCDF(m, v) или CDF = stats::poissonCDF(m) с подходящими численными значениями mV возможны и рекомендованы.
Распределения, которые не обеспечиваются stats- пакет может быть реализован легко пользователем. Определяемая пользователем процедура f может реализовать любую функцию распределения. В случае CDF, stats::csGOFT вызовы f с граничными значениями a i, b i ячеек, чтобы вычислить вероятности ячейки через p i = f (b i) - f (a i) (автоматически установка f (a 1) = 0 и f (b k) = 1).
Функциональный f должен возвратить числовое действительное значение между 0 и 1. Смотрите Пример 5 и Пример 6.
В качестве альтернативы функциональный f может быть задан одномерным арифметическим выражением g (x) в зависимости от символьной переменной x. Это интерпретировано как функция![]() . См. Пример 6.
. См. Пример 6.
Смотрите раздел 'Background' этой страницы справки для получения дополнительной информации о спецификации распределения через CDF = f, PDF = f или PF = f.
Вызов stats::csGOFT(data, cells, X = f) возвращает список [PValue = p, StatValue = s, MinimalExpectedCellFrequency = m]:
s наблюдаемая величина статистической величины хи-квадрата
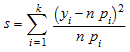 ,
,
где n является объемом выборки, k является количеством ячеек, y i является наблюдаемой частотой ячейки данных (т.е. y, i является количеством данных x j, попадающий в ячейку c i), и p, i является ячейкой probabilitiy соответствие предполагавшемуся распределению f.
p является наблюдаемым уровнем значения статистической величины хи-квадрата с k - 1 степенью свободы, т.е. p = 1 - stats:: chisquareCDF (k - 1) (s)
![]() минимум ожидаемых частот ячейки n pi. Эта информация предоставляется тестом, чтобы убедиться, что граничные условия для “разумного” разделения ячейки соблюдают (см. раздел “Background” этой страницы справки).
минимум ожидаемых частот ячейки n pi. Эта информация предоставляется тестом, чтобы убедиться, что граничные условия для “разумного” разделения ячейки соблюдают (см. раздел “Background” этой страницы справки).
Наиболее релевантная информация возвращена stats::csGOFT наблюдаемый уровень значения PValue = p. Это должно быть интерпретировано следующим образом: По нулевой гипотезе, статистической величине хи-квадрата
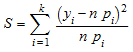
приблизительно распределенный хи-квадрат (для больших выборок):
![]() .
.
По нулевой гипотезе вероятность p = Pr (S> s) не должен быть малым, где s значение статистической величины, достигнутой выборкой.
А именно, p = Pr (S> s) ≥ α должен содержать для данного уровня 0 значения <α <1, Если это условие нарушено, гипотеза может быть отклонена на уровне α.
Таким образом, если PValue (наблюдаемый уровень значения) p = Pr (S> s) удовлетворяет p <α, демонстрационное продвижение к наблюдаемой величине s из статистического S представляет маловероятное событие, и нулевая гипотеза может быть отклонена на уровне α.
С другой стороны, значения p близко к 1 должны вызвать подозрение о случайности данных: они указывают на подгонку, которая слишком хороша.
Функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.
Мы рассматриваем случайные данные, которые должны быть нормально распределены со средним значением 15 и отклонение 2:
f := stats::normalRandom(15, 2, Seed = 0): data := [f() $ i = 1..1000]:
Согласно рекомендациям в разделе 'Background' этой страницы справки, количество ячеек должно быть приблизительно![]() , где n = 1000 является объемом выборки.
, где n = 1000 является объемом выборки.
Мы хотим использовать 32 ячейки, которые равновероятны относительно предполагавшегося нормального распределения. Мы оцениваем средний m и отклонение v данных:
[m, v] := [stats::mean(data), stats::variance(data, Sample)]
![]()
Служебная функция stats::equiprobableCells используется для расчета равновероятное разделение ячейки через функцию квантиля нормального распределения эмпирическими параметрами:
cells := stats::equiprobableCells(32, stats::normalQuantile(m, v)): stats::csGOFT(data, cells, CDF = stats::normalCDF(m, v))
![]()
Наблюдаемый уровень значения![]() , достигнутый выборкой, не мал. Следовательно, не нужно отклонять гипотезу, что выборка нормально распределена со средним значением
, достигнутый выборкой, не мал. Следовательно, не нужно отклонять гипотезу, что выборка нормально распределена со средним значением![]() и отклонением
и отклонением![]() .
.
В следующем, мы impurify выборка путем добавления некоторых равномерно распределенных чисел. Вычисляется новая равновероятная ячейка, делящая подходящий для новых данных:
r := stats::uniformRandom(10, 20, Seed = 0): data := append(data, r() $ 40): [m, v] := [stats::mean(data), stats::variance(data, Sample)]: k := round(2*nops(data)^(2/5)): cells := stats::equiprobableCells(k, stats::normalQuantile(m, v)): stats::csGOFT(data, cells, CDF = stats::normalCDF(m, v))
![]()
Изменяемые данные могут быть отклонены как нормально распределенная выборка на уровнях, столь же небольших как![]() .
.
delete f, data, m, v, k, cells, r:
Мы создаем выборку случайных данных, которые должны быть биномиальным образом распределены испытательным параметром 70 и параметром вероятности![]() :
:
r := stats::binomialRandom(70, 1/2, Seed = 123): data := [r() $ k = 1..1000]:
Со значением ожидания 35 и стандартным отклонением![]() этого распределения, мы ожидаем, что большинство данных будет иметь значения между 30 и 40. Таким образом, разделение ячейки, состоящее из 12 ячеек, соответствующих интервалам
этого распределения, мы ожидаем, что большинство данных будет иметь значения между 30 и 40. Таким образом, разделение ячейки, состоящее из 12 ячеек, соответствующих интервалам
![]()
должно быть соответствующим. Обратите внимание на то, что все ячейки интерпретированы как интервалы![]() , т.е. левый контур не включен в интервал. Строго говоря значение 0 не покрыто этими ячейками. Однако с
, т.е. левый контур не включен в интервал. Строго говоря значение 0 не покрыто этими ячейками. Однако с CDF спецификация, stats::csGOFT игнорирует крайний левый контур и заменяет его -infinity. Таким образом объединение ячеек действительно покрывает все целые числа 0, …, 70, который может быть достигнут предполагавшимся биномиальным распределением 'испытательным параметром' 70:
cells := [[0, 30], [i, i + 1] $ i = 30..39, [40, 70]]
![]()
Мы применяем χ 2 теста с различными спецификациями биномиального распределения. Они все приводят к тому же результату. Однако первый вызов с помощью CDF спецификация является самым эффективным (самым быстрым) вызовом:
stats::csGOFT(data, cells, CDF = stats::binomialCDF(70, 1/2));
![]()
stats::csGOFT(data, cells, PF = stats::binomialPF(70, 1/2));
![]()
f := binomial(70, x)*(1/2)^x*(1/2)^(70 - x): stats::csGOFT(data, cells, PF = f)
![]()
Наблюдаемый уровень значения![]() указывает, что данные проходят тест хорошо.
указывает, что данные проходят тест хорошо.
Затем мы любим до безумия выборку путем добавления значения 35 сорок раз:
data := data . [35 $ 40]: stats::csGOFT(data, cells, CDF = stats::binomialCDF(70, 1/2));
![]()
Теперь данные могут быть отклонены как биномиальная выборка заданными параметрами на уровнях, столь же небольших как![]() .
.
delete r, data, cells, f:
Мы тестовые данные, которые подразумевают быть выборкой беты, распределили числа с масштабными коэффициентами 3 и 2. Поскольку бета отклоняется, достигают значений между 0 и 1, мы выбираем равноотстоящее разделение ячейки интервала [0, 1] состоящий из 10 ячеек. Различные эквивалентные вызовы stats::csGOFT продемонстрированы:
r := stats::betaRandom(3, 2, Seed = 1): data := [r() $ i = 1..100]: cells := [[(i - 1)/10, i/10] $ i = 1..10]: stats::csGOFT(data, cells, CDF = stats::betaCDF(3, 2)); stats::csGOFT(data, cells, CDF = (x -> stats::betaCDF(3, 2)(x)))
![]()
![]()
В качестве альтернативы бета распределение может быть передано PDF спецификация. Это, однако, менее эффективно, чем CDF спецификация, используемая прежде:
stats::csGOFT(data, cells, PDF = stats::betaPDF(3, 2)); stats::csGOFT(data, cells, PDF = (x -> stats::betaPDF(3, 2)(x)));
![]()
![]()
Наблюдаемый уровень значения![]() не мал. Следовательно, этот тест не указывает, что данные должны быть отклонены как бета распределенная выборка заданными параметрами. Обратите внимание, однако, что минимальная ожидаемая частота ячейки, данная третьим элементом возвращенного списка, скорее мала. Это указывает, что разделение ячейки не очень удачно. Мы исследуем ожидаемые частоты ячейки путем вычисления n pi = n (f (b i) - f (a i)), где f является кумулятивной функцией распределения бета распределения, и n является объемом выборки:
не мал. Следовательно, этот тест не указывает, что данные должны быть отклонены как бета распределенная выборка заданными параметрами. Обратите внимание, однако, что минимальная ожидаемая частота ячейки, данная третьим элементом возвращенного списка, скорее мала. Это указывает, что разделение ячейки не очень удачно. Мы исследуем ожидаемые частоты ячейки путем вычисления n pi = n (f (b i) - f (a i)), где f является кумулятивной функцией распределения бета распределения, и n является объемом выборки:
f:= stats::betaCDF(3, 2): map(cells, cell -> 100*(f(cell[2]) - f(cell[1])))
![]()
Эти значения показывают, что первые две или три ячейки должны быть соединены с отдельной ячейкой. Мы изменяем разделение ячейки путем присоединения первых трех и последних двух ячеек:
cells := [[0, 3/10], [(i - 1)/10, i/10] $ i = 4..8, [8/10, 1]]
![]()
Для этого разделения ячейки ожидаемые частоты в случайной выборке размера 100 являются достаточно большими для всех ячеек:
map(cells, cell -> 100*(f(cell[2]) - f(cell[1])))
![]()
Мы применяем другой χ 2 теста с этим улучшенным разделением:
stats::csGOFT(data, cells, CDF = f)
![]()
Снова, с наблюдаемым уровнем значения![]() , тест не дает подсказки, что данные не являются бетой, распределенной заданными параметрами.
, тест не дает подсказки, что данные не являются бетой, распределенной заданными параметрами.
Теперь мы тестируем, могут ли данные быть расценены как являющийся нормально распределенным. Во-первых, мы оцениваем параметры (среднее значение и отклонение) требуемый для нормального распределения:
[m, v] := [stats::mean(data), stats::variance(data, Sample)]
![]()
Разделение ячейки, используемое прежде, было разделением интервала [0, 1], потому что бета отклоняется, достигают значений в этом интервале. Теперь мы создаем разделение 7 равновероятных ячеек с помощью функции квантиля нормального распределения:
k := 7: cells := stats::equiprobableCells(7, stats::normalQuantile(m, v))

Действительно, ячейки тезисов равновероятны:
f:= stats::normalCDF(m, v): map(cells, cell -> f(cell[2]) - f(cell[1]))
![]()
Мы тестируем на нормальность с предполагаемым средним значением и отклонением:
stats::csGOFT(data, cells, CDF = f)
![]()
С наблюдаемым уровнем значения ![]() данные не должны быть отклонены как нормально распределенная выборка. Мы отмечаем, что непараметрический тест Шапиро-Вилка реализовал в
данные не должны быть отклонены как нормально распределенная выборка. Мы отмечаем, что непараметрический тест Шапиро-Вилка реализовал в stats::swGOFT действительно обнаруживает ненормальность выборки:
stats::swGOFT(data)
![]()
С наблюдаемым уровнем значения ![]() нормальность может быть отклонена на уровнях настолько же низко как
нормальность может быть отклонена на уровнях настолько же низко как![]() .
.
delete r, data, cells, f, m, v, k, boundaries:
Мы демонстрируем использование выборок типа stats::sample. Мы создаем выборку, состоящую из одного столбца строки и двух столбцов нестроки:
s := stats::sample( [["1996", 1242, 156], ["1997", 1353, 162], ["1998", 1142, 168], ["1999", 1201, 182], ["2001", 1201, 190], ["2001", 1201, 190], ["2001", 1201, 205], ["2001", 1201, 210], ["2001", 1201, 220], ["2001", 1201, 213], ["2001", 1201, 236], ["2001", 1201, 260], ["2001", 1201, 198], ["2001", 1201, 236], ["2001", 1201, 245], ["2001", 1201, 188], ["2001", 1201, 177], ["2001", 1201, 233], ["2001", 1201, 270]])
"1996" 1242 156 "1997" 1353 162 "1998" 1142 168 "1999" 1201 182 "2001" 1201 190 "2001" 1201 190 "2001" 1201 205 "2001" 1201 210 "2001" 1201 220 "2001" 1201 213 "2001" 1201 236 "2001" 1201 260 "2001" 1201 198 "2001" 1201 236 "2001" 1201 245 "2001" 1201 188 "2001" 1201 177 "2001" 1201 233 "2001" 1201 270
Мы рассматриваем данные в третьем столбце. Среднее значение и отклонение этих данных вычисляются:
[m, v] := float([stats::mean(s, 3),
stats::variance(s, 3, Sample)])![]()
Мы проверяем, нормально распределены ли данные третьего столбца с эмпирическим средним значением и отклонением, вычисленным выше. Мы вычисляем соответствующую ячейку, делящую таким же образом, как объяснено в Примере 1:
samplesize := s::dom::size(s): k := round(2*samplesize^(2/5)): cells := stats::equiprobableCells(k, stats::normalQuantile(m, v)): stats::csGOFT(s, 3, cells, CDF = stats::normalCDF(m, v))
![]()
Таким образом данные проходят тест.
delete s, m, v, samplesize, k, cells:
Мы демонстрируем, как могут использоваться пользовательские функции распределения. Умирание прокручивается 60 раз. Следующие частоты баллов 1, 2, …, 6 наблюдаются:
score | 1 | 2 | 3 | 4 | 5 | 6 ----------+---+----+---+----+---+-- frequency | 7 | 16 | 8 | 17 | 3 | 9
Мы тестируем нулевую гипотезу, что dice справедлив. В соответствии с этой гипотезой, переменная X, данная счетом одного списка, достигает значений 1 - 6 с постоянной вероятностью![]() . В настоящее время,
. В настоящее время, stats- пакет не обеспечивает дискретное равномерное распределение, таким образом, мы реализуем соответствующую совокупную функцию дискретного распределения f:
f := proc(x)
begin
if x < 0 then
0
elif x <= 6 then
trunc(x)/6
else 1
end_if;
end_proc:Мы создаем данные, представляющие 60 списков:
data := [ 1 $ 7, 2 $ 16, 3 $ 8, 4 $ 17, 5 $ 3, 6 $ 9]:
Мы выбираем набор ячеек, каждая из которых содержит точно одно из целых чисел 1, …, 6:
Wir wählen sodann eine Zellzerlegung, таким образом, dass jede Zelle genau eine der ganzen Zahlen 1, …, 6 enthält:
cells := [[i - 1/2, i + 1/2] $ i = 1..6]
![]()
stats::csGOFT(data, cells, CDF = f)
![]()
На уровне значения всего![]() , нулевая гипотеза 'dice справедлива', должен быть отклонен.
, нулевая гипотеза 'dice справедлива', должен быть отклонен.
delete f, data, cells:
Мы даем дальнейшую демонстрацию пользовательских функций распределения. Следующая процедура представляет кумулятивную функцию распределения![]() переменной X, поддержанной на интервале
переменной X, поддержанной на интервале![]() . Это будет вызвано значениями от границ ячейки и должно возвратить численные значения между 0 и 1:
. Это будет вызвано значениями от границ ячейки и должно возвратить численные значения между 0 и 1:
f := proc(x)
begin
if x <= 0 then return(0)
elif x <= 1 then return(x^2)
else return(1)
end_if
end_proc:Мы тестируем гипотезу, что следующими данными является f - распределенный. Ячейки формируют равноотстоящее разделение интервала [0, 1]:
data := [sqrt(frandom()) $ i = 1..10^3]: k := 10: cells := [[(i - 1)/k, i/k] $ i = 1..k]: stats::csGOFT(data, cells, CDF = f)
![]()
Тест не дисквалифицирует выборку, как являющуюся f - распределенный. Действительно, для универсальной формы отклоняют Y на интервале [0, 1] (как произведено frandom), кумулятивная функция распределения![]() действительно дана f.
действительно дана f.
Мы отмечаем, что предыдущая функция дает к правильным значениям CDF для всех действительных аргументов. Выбранное разделение ячейки указывает, что только значения от интервала![]() рассматриваются. Начиная с
рассматриваются. Начиная с stats::csGOFT только оценивает CDF на границах ячейки, чтобы вычислить вероятность ячейки ячейки![]() f (b) - f (a), это достаточно, чтобы ограничить f интервалом
f (b) - f (a), это достаточно, чтобы ограничить f интервалом![]() . Следовательно, для выбранных ячеек, символьное выражение
. Следовательно, для выбранных ячеек, символьное выражение f = x^2 может также использоваться, чтобы задать распределение:
stats::csGOFT(data, cells, CDF = x^2)
![]()
delete f, data, k, cells:
|
Статистические данные: действительные численные значения |
|
Выборка доменного типа |
|
Целое число, представляющее индекс столбца демонстрационного |
|
Границы ячейки: вещественные числа, удовлетворяющие a 1 <b 1 ≤ a 2 <b 2 ≤ a 3 <…. Также |
|
Процедура, представляющая предполагавшееся распределение: любой кумулятивная функция распределения ( |
|
Это определяет как процедура |
список трех уравнений
[PValue = p, StatValue = s, MinimalExpectedCellFrequency = m]
со значениями с плавающей точкой pSM. Смотрите раздел “Details” ниже для интерпретации этих значений.
В Р.Б. Д'Агостино и М.А. Стивенсе, “Методы Качества подгонки”, Марсель Деккер, 1986, p. 70-71, каждый находит следующие рекомендации для выбора разделения ячейки:
Количество используемых ячеек должно быть приблизительно![]() , где n является объемом выборки.
, где n является объемом выборки.
Ячейки должны иметь равные вероятности p i при предполагавшемся распределении.
С равновероятными ячейками средним значением ожидаемых частот ячейки n pi должен быть по крайней мере 1 при тестировании на уровне значения α = 0.05. Для α = 0.01, средней ожидаемой частотой ячейки должен быть, по крайней мере, 2. Когда ячейки не приблизительно равновероятны, средняя ожидаемая частота ячейки для уровней значения выше должна быть удвоена. Например, средней ожидаемой частотой ячейки на уровне значения α = 0.01 должен быть, по крайней мере, 4.
Функция распределения f передала stats::csGOFT через X = f только используется для расчета вероятности ячейки p i = Pr (a i <x ≤ b i) ячеек![]() .
.
Кумулятивная функция распределения f заданный CDF = f используется для расчета вероятности ячейки через p i = f (b i) - f (a i).
Функция плотности вероятности f заданный через PDF = f используется для расчета вероятности ячейки через численное интегрирование![]() :. это довольно дорого!
:. это довольно дорого!
Функция дискретной вероятности задана через PF = f используется для расчета вероятности ячейки через суммирование![]() .
.
Таким образом, со спецификацией PF = f, распределение, как неявно предполагается, поддерживается на целых числах в ячейках![]() . Не используйте
. Не используйте PF = f если функция дискретной вероятности не поддерживается на целых числах! Используйте CDF = f с соответствующей (дискретной) кумулятивной функцией распределения вместо этого!
Со спецификацией PF = f, значение - ∞ не допускают для левого контура a 1 из первой ячейки c 1 = Intval ([a 1], [b 1]).