stats::normalRandomСгенерируйте генератор случайных чисел для нормальных отклонений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
stats::normalRandom(m, v, <Seed = s>)
stats::normalRandom(m, v) возвращает процедуру, которая производит нормальные отклонения (случайные числа) со средним m и отклонением v> 0.
Процедура f := stats::normalRandom(m, v) может быть назван в форме f(). Возвращаемое значение f() или число с плавающей запятой или символьное выражение:
Если m и v может быть преобразован в числа с плавающей запятой, f() возвращает действительное число с плавающей точкой. В противном случае, символьный вызов stats::normalRandom(m, v)() возвращен.
Численные значения m и v только приняты, если они действительны, и v положителен.
Значения X = f() распределяются случайным образом согласно кумулятивной функции распределения нормального распределения параметрами m и v. Для любого действительного x, вероятность, что X ≤ x дают
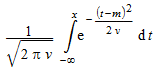 .
.
Без опции Seed = s, начальный seed выбран внутренне. Этот начальный seed установлен в значение по умолчанию, когда MuPAD® запускается. Таким образом каждый раз MuPAD запускается или повторно инициализируется с reset функция, случайные генераторы производят те же последовательности чисел.
В отличие от функционального random, генераторы производятся stats::normalRandom не реагируйте на переменную окружения SEED.
Для КПД рекомендуется произвести последовательности случайных чисел K через
f := stats::normalRandom(m, v): f() $k = 1..K;
вместо
stats::normalRandom(m, v)() $k = 1..K;
Последний вызов производит последовательность генераторов, каждый из которых называется однажды. Также отметьте это
stats::normalRandom(m, v, Seed = n)() $k = 1..K;
не производит случайную последовательность, потому что последовательность недавно инициализированных генераторов была бы создана каждый из них производящий тот же номер.
Функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.
Мы генерируем нормальные отклонения со средним значением 2 и отклонение![]() :
:
f := stats::normalRandom(2, 3/4): f() $ k = 1..4
![]()
delete f:
Символьными параметрами никакие случайные числа с плавающей запятой не могут быть произведены:
f := stats::normalRandom(m, v): f()
![]()
Когда m и v оценивают к вещественным числам, f начинает производить случайные числа с плавающей точкой:
m := PI: v := 1/8: f() $ k = 1..4
![]()
delete f, m, v:
Мы используем опцию Seed = s воспроизвести последовательность случайных чисел:
f := stats::normalRandom(PI, 3, Seed = 1): f() $ k = 1..4
![]()
g := stats::normalRandom(PI, 3, Seed = 1): g() $ k = 1..4
![]()
f() = g(), f() = g()
![]()
delete f, g:
|
Среднее значение: арифметическое выражение, представляющее действительное значение |
|
Отклонение: арифметическое выражение, представляющее положительное действительное значение |
|
Опция, заданная как Инициализирует случайный генератор с целочисленным seed Эта опция служит для генерации генераторов, которые возвращают предсказуемые последовательности псевдослучайных чисел. Генератор инициализируется с seed Когда эта опция используется, параметры |
Реализованный алгоритм для расчета нормальных отклонений использует метод Поля-Mueller. Для получения дополнительной информации см.: Д. Нут, Получисловые Алгоритмы (1998), Издание 2, стр 122.