Документация

Параллельный набор

Предположим данные, которые вы хотите собрать, сгенерирован поэлементно, и вы знаете заранее, сколько элементов будет сгенерировано. Интуитивный подход для сбора таких данных должен создать пустой список и добавить каждый новый элемент в конец списка. Например, эта процедура использует этот подход, чтобы собрать случайные целые числа, сгенерированные random:

col :=
proc(n)
  local L, i;
begin
  L := [];
  for i from 1 to n do
    L := L.[random()];
  end_for;
end:

Процедура генерирует случайные целые числа и собирает их в списке:

col(5)

Чтобы оценить производительность этого подхода, используйте процедуру col сгенерировать список 50 000 случайных чисел:

time(col(50000))

time функция возвращает результаты, измеренные в миллисекундах.

Теперь проверяйте, сколько времени процедура на самом деле проводит генерирующиеся случайные числа:

time(random() $ i = 1..50000)

Таким образом процедура тратит наиболее часто добавление недавно сгенерированных чисел к списку. В MuPAD^®, добавляя новую запись в список n записи занимают время пропорциональные n. Поэтому время выполнения col(n) пропорционально n ². Можно визуализировать эту зависимость путем графического вывода времен что col(n) тратит при создании списков 1 - 50 000 записей:

plotfunc2d(n -> time(col(n)), n = 1..50000,
               Mesh = 20, AdaptiveMesh = 0)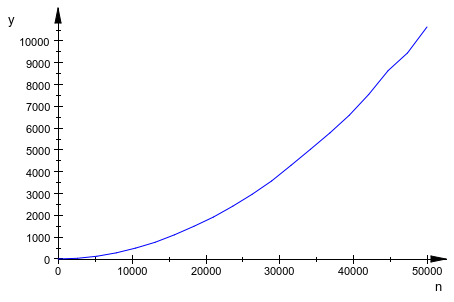

При добавлении новой записи в список MuPAD выделяет место для нового, более длинного списка. Затем это копирует все записи старого списка плюс новая запись в этот новый список. Более быстрый подход должен создать целый список целиком, не добавляя каждую новую запись отдельно. Этот подход называется параллельным набором, потому что вы создаете и собираете данные одновременно. Используйте оператор последовательности $ реализовывать этот подход:

col := proc(n)
  local i;
begin
  [random() $ i = 1..n];
end:

Эта процедура проводит большую часть своего времени, генерируя случайные числа:

time(col(50000))

Набор фиксированной длины

Предположим, что вы знаете, сколько элементов вы сгенерируете, но вы не можете сгенерировать их целиком. В этом случае лучшая стратегия состоит в том, чтобы создать список необходимой длины, заполняющей его некоторой константой, такой как 0 или NIL. Затем можно заменить любую запись этого списка со сгенерированным значением. В этом случае вы не должны генерировать элементы в порядке, в котором вы хотите, чтобы они появились в списке.

Например, используйте эту процедуру, чтобы сгенерировать список первого n Лукас нумерует. Процедура создает список n записи, где каждая запись 0. Затем это присваивает значения первым двум записям. Чтобы заменить все другие записи списка с числами Лукаса, процедура использует for цикл:

lucas :=
proc(n)
  local L, i;
begin
  L := [0 $ n];
  L[1] := 1;
  L[2] := 3;
  for i from 3 to n do
    L[i] := L[i-1] + L[i-2];
  end_for;
  L
end:

Измерьтесь время должно было создать список 10 000 чисел Лукаса:

time(lucas(10000))

Если вы используете процедуру, которая создает пустой список и добавляет, каждый сгенерировал номер Лукаса к этому списку, то создание списка 10 000 чисел Лукаса берет намного дольше:

lucas :=
proc(n)
  local L, i;
begin
  L := [];
  L :=L.[1];
  L := L.[3];
  for i from 3 to n do
    L := L.[L[i-1] + L[i-2]];
  end_for;
  L
end:

time(lucas(10000))

Набор "известная максимальная длина"

Если вы не можете предсказать число элементов, которое вы сгенерируете, но иметь разумный верхний предел этого номера, использовать эту стратегию:

Например, используйте следующую процедуру, чтобы создать список. Записи этого списка являются модульными квадратами номера a (a ² ультрасовременных n). Вы не можете предсказать количество записей в получившемся списке, потому что это зависит от параметров a и n. Тем не менее, вы видите, что в этом случае количество записей в списке не может превысить n:

modPowers :=
proc(a, n)
  local L, i;
begin
  L := [0 $ n];
  L[1] := a;
  L[2] := a^2 mod n;
  i := 2;
  while L[i] <> a do
    L[i + 1] := a*L[i] mod n;
    i := i + 1;
  end_while;
  L := L[1..i - 1];
end:

Когда вы вызываете modPowers для a = 3 и a = 2, это создает два списка различных длин:

modPowers(3, 14);
modPowers(2, 14)

Набор неизвестной максимальной длины

Часто, вы не можете предсказать число элементов и не можете оценить верхний предел этого номера, прежде чем вы начнете генерировать фактические данные. Один способ иметь дело с этой проблемой состоит в том, чтобы выбрать некоторый верхний предел и использовать стратегию, описанную в Известном Максимальном Наборе Длины. Если тот предел достигнут, то:

Как правило, увеличение длины списка постоянным множителем приводит к лучшей производительности, чем увеличение его постоянным количеством записей:

rndUntil42 :=
proc()
  local L, i;
begin
  i := 1;
  L := [random()];
  while L[i] mod 42 <> 0 do
    if i = nops(L) then
      L := L.L;
    end_if;
    i := i+1;
    L[i] := random();
  end_while;
  L[1..i];
end:

SEED := 123456789:
rndUntil42()

SEED := 123456789:
time(rndUntil42() $ i = 1..500)

В качестве альтернативы, если вы не можете предсказать число элементов, которое необходимо будет собрать, затем использовать table это растет автоматически (хэш-таблица):

rndUntil42 :=
proc()
  local L, i, j;
begin
  i := 1;
  L := table(1 = random());
  while L[i] mod 42 <> 0 do
    i := i+1;
    L[i] := random();
  end_while;
  [L[j] $ j=1..i];
end:

SEED := 123456789:
time(rndUntil42() $ i = 1..500)

В данном примере использование таблицы немного быстрее. Если вы изменяете значение 42 в другое значение, использование списка может быть быстрее. В общем случае таблицы предпочтительны, когда вы собираете большие объемы данных. Выберите подход, который работает лучше всего на решение вашей задачи.