Документация

Дифференцируйте функции

Чтобы вычислить производные функций, используйте дифференциальный оператор D. Этот оператор дифференцирует и стандартные математические функции и ваши собственные функции, созданные в MuPAD^®. Например, найдите первые производные следующих стандартных математических функций реализованными в MuPAD:

D(sin), D(exp), D(cosh), D(sqrt), D(heaviside)

Создайте свою собственную функцию с одной переменной и вычислите производную этой функции:

f := x -> x^3:
D(f)

В качестве альтернативы используйте ' как ярлык для дифференциального оператора D:

f := x -> sin(x)/x^2:
f';
f'(x)

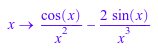
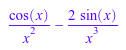
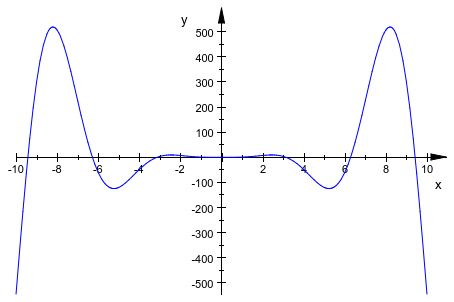
Вычисление первых производных функции позволяет вам найти ее локальные экстремальные значения (минимумы и максимумы). Например, создайте эту функцию и постройте ее на интервале -10 < x < 10:

F := x -> x^3*sin(x);
plot(F, x = -10..10)

Найдите локальные экстремальные значения F на интервале -10 < x < 10. Если точка является локальным экстремальным значением (или минимум или максимум), первая производная функции в той точке равняется 0. Поэтому найти локальные экстремальные значения F, решите уравнение F'(x) = 0. Используйте AllRealRoots опция, чтобы возвратить больше чем одно решение.

extrema := numeric::solve(F'(x) = 0, x = -10..10, AllRealRoots)

Теперь вычислите соответствующие значения F. Например, вычислите F для третьего элемента, -2.455643863, в наборе решения:

F(extrema[3])

Вычислить значения F для всех локальных минимумов и максимумов, используйте следующую команду. Здесь, $ используется, чтобы оценить F для каждого элемента extrema набор.

points := {[x, F(x)] $ x in extrema}

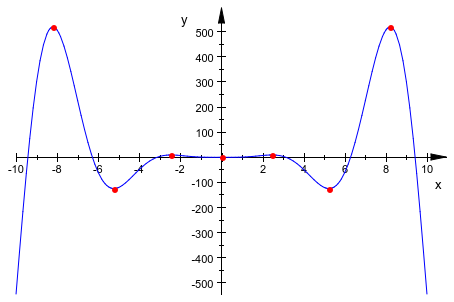
Функция построения графика F с экстремальными точками:

plot(F, points, x = -10..10)

Чтобы вычислить производную многомерной функции, задайте переменную дифференцирования. Оператор D не принимает имена переменных. Вместо того, чтобы обеспечить имя переменной, обеспечьте его индекс. Например, интегрируйте следующую функцию относительно ее первой переменной x. Затем интегрируйте функцию относительно ее второй переменной y:

f := (x, y) -> x^2 + y^3:
D([1], f);
D([2], f)

Список индексов, принятых оператором D относится к порядку, в котором вы обеспечили переменные при создании функции:

f := (x, y) -> x^2 + y^3:
D([1], f);
f := (y, x) -> x^2 + y^3:
D([1], f)

Чтобы найти вторым - и частные производные высшего порядка функции, используйте тот же индекс два или больше раза. Например, вычислите частные производные второго порядка относительно x и относительно y:

f := (x, y) -> x^3*sin(y):
D([1, 1], f);
D([2, 2], f)

Чтобы вычислить второй - и производные высшего порядка относительно нескольких переменных (смешанные производные), предоставьте список индексов переменных дифференцирования:

f := (x, y) -> x^3*sin(y):
D([1, 2], f);