Взаимодействия среды

D использование option remember.

Пример 1

D(f) вычисляет производную функционального f:

D(sin), D(x -> x^2), D(id)

D также работает на более комплексные функциональные выражения:

D(sin @ exp + 2*(x -> x*ln(x)) + id^2)

Если f идентификатор без значения, символьного D на звонок отвечают:

delete f: D(f + sin)

То же самое содержит для объектов типа ядра, который не может рассматриваться как функции:

D(NIL)

f' сокращение для D(f):

(f + sin)', (x -> x^2)', id'

Пример 2

Константы рассматриваются как постоянные функции:

PI', 3', (1/2)'

Пример 3

Обычные правила дифференцирования реализованы. Обратите внимание на то, что списки и наборы могут также быть взяты в качестве входа; в этом случае, D применяется к каждому элементу списка или устанавливается:

delete f, g: D([f+g, f*g]); D({1/f, f@g})

Пример 4

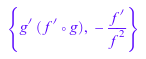
Производные большинства специальных функций библиотеки могут быть вычислены. Снова, id обозначает тождественное отображение:

D(tan); D(sin*cos); D(1/sin); D(sin@cos); D(2*sin + ln)

Пример 5

D может также вычислить производные процедур:

f := x -> x^2:
g := proc(x) begin tan(ln(x)) end:
D(f), D(g)

Мы дифференцируем функцию двух аргументов путем передачи списка индексов в качестве первого аргумента к D. В примере ниже, мы сначала дифференцируемся относительно второго аргумента и затем дифференцируем результат относительно первого аргумента:

D([1, 2], (x, y) -> sin(x*y))

Порядок частных производных не релевантен:

D([2, 1], (x, y) -> sin(x*y))

delete f, g:

Пример 6

Полином рассматривается как полиномиальная функция:

D(poly(x^2 + 3*x + 2, [x]))

Мы дифференцируем следующий двумерный полиномиальный f дважды относительно его второй переменной y и однажды относительно его первой переменной x:

f := poly(x^3*y^3, [x, y]):
D([1, 2, 2], f) = diff(f, y, y, x)

delete f:

Пример 7

Вложенные вызовы D сглажены:

D([1], D([2], f))

Однако это не содержит для вызовов только с одним аргументом, начиная с D(f) и D([1], f) не считаются тем же самым:

D(D(f))

Пример 8

D май только быть примененным к функциям, тогда как diff имеет только смысл для выражений:

D(sin), diff(sin(x), x)

Применение D к выражениям и diff к функциям не имеет никакого смысла:

D(sin(x)), diff(sin, x)

rewrite позволяет переписывать выражения с D в diffВыражение:

rewrite(D(f)(y), diff), rewrite(D(D(f))(y), diff)

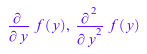
Обратная конверсия возможна также:

map(%, rewrite, D)

Пример 9

Иногда вам, возможно, понадобится n-th производная функции, где n неизвестен. Это может быть достигнуто с помощью повторного оператора состава. Например, давайте запишем функцию, которая вычисляет k-th полином Тейлора функционального f в точке x ₀ и использует x в качестве переменной для того полинома:

kthtaylorpoly:=
(f, k, x, x0) -> _plus(((D@@n)(f)(x0) * (x - x0)^n / n!) $ n = 0..k):
kthtaylorpoly(sin, 7, x, 0)

delete kthtaylorpoly:

Пример 10

Опытные пользователи могут расширить D к их собственным специальным математическим функциям (см. раздел “Background” ниже). С этой целью встройте свою математическую функцию f, скажем, в функцию environmentf и реализуйте поведение D для этой функции как "D" паз функциональной среды. Паз должен обработать два случая: это может быть или вызвано только одним аргументом, который равняется f, или с двумя аргументами, где второй равняется f. В последнем случае первый аргумент является списком произвольных много индексов; то есть, паз должен смочь обработать более высокие частные производные также.

Предположим, например, что нам дают функциональный f (t, x, y), и что мы ничего не знаем о f за исключением того, что это дифференцируемо бесконечно часто и удовлетворяет дифференциальному уравнению с частными производными. Заставить MuPAD устранить производные относительно t, мы можем сделать следующее:

f := funcenv(f):
f::D :=
proc(indexlist, ff)
  local
    n        : DOM_INT,   // Number of t-derivatives.
    list_2_3 : DOM_LIST;  // List of indices of 2's and 3's.
                          // These remain unchanged.
begin
  if args(0) <> 2 then
    error("Wrong number of arguments")
  end_if;
  n        :=  nops(select(indexlist, _equal, 1));
  list_2_3 :=  select(indexlist, _unequal, 1);
  // rewrite (d/dt)^n = (d^2/dx^2 + d^2/dy^2)^n
  _plus(binomial(n, k) *
        hold(D)(sort([2 $ 2*(n-k), 3 $ 2*k].list_2_3), ff)
        $ k = 0..n)
end_proc:

Теперь частные производные относительно первого аргумента t переписаны производными относительно второго и третьего аргумента:

D([1], f^2)(t, x, y)

D([1, 2, 1], f)

delete f:

Возвращаемые значения

функционируйте или функциональное выражение. Если f массив или список и т.д., соответствующий объект, содержащий производные записей, возвращен.

Перегруженный

f