Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Символьные решения могут быть возвращены в различных, но математически эквивалентных формах. MuPAD® постоянно улучшает свою функциональность, включая решатели и simplifiers. Эти улучшения могут заставить различные релизы MuPAD возвращать различные формы тех же символьных выражений. Например, когда вы решаете уравнение
eq := ode({y''(t)=-a^2*y(t), y(0)=1, y'(PI/a)=0}, y(t)):MuPAD 5.1 (R2008b) возвращается:
solution := solve(eq): eval(solution) assuming a <> 0
![]()
Для того же уравнения возвращается MuPAD 5.2 (R2009a):
solution := solve(eq): eval(solution) assuming a <> 0
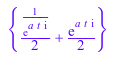
testeq не может сравнить наборы. Чтобы протестировать математическое равенство решений, возвращенных как наборы, сравните каждую пару решений индивидуально.
Если возвращенное решение отличается от того, что вы ожидаете, тестируете математическое равенство решений:
testeq(cos(a*t), (1/exp(a*t*I))/2 + exp(a*t*I)/2)
![]()
Проверка решений с произвольными постоянными может быть намного более сложной, чем проверка простых решений без констант. В таких решениях рассмотрите произвольные постоянные как символьные параметры. В простых случаях можно принять, что параметры равны. Например, решите следующее обыкновенное дифференциальное уравнение. Форма возвращенного решения зависит от типа уравнения. Решатель может идентифицировать уравнение с различными типами уравнения:
reset()
o:= ode(y'(x) = (- 1/x + 2*I)*y(x) + 1/x*y(x)^2, y(x)): o1 := solve(o)
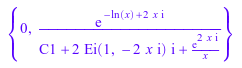
Если вы явным образом задаете тип как Бернулли, решатель возвращает другую форму результата:
o2 := solve(o, Type = Bernoulli)
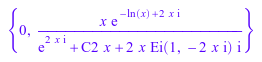
Проверяйте равенство этих двух решений путем вызова testeq команда для каждой пары решений. Помните тот testeq не может сравнить наборы.
testeq(o1[1], o2[1]), testeq(o1[2], o2[2])
![]()
Второе решение возвращает FALSE потому что testeq не знает тот C2 и C3 произвольные постоянные. Когда вы явным образом принимаете равенство констант, testeq подтверждает, что решения математически равны:
testeq(o1[1], o2[1]) assuming C1 = C2, testeq(o1[2], o2[2]) assuming C1 = C2
![]()
Проверка математического равенства результатов путем предположения, что произвольные постоянные равны, не всегда работает. Решатель может выбрать произвольные постоянные, чтобы представлять различные выражения. Например, одна форма решения может включать C1, и другая форма того же решения может включать![]() . В этом случае необходимо принять это
. В этом случае необходимо принять это![]() .
.
Если результаты включают произвольные постоянные, число элементов в наборе решения может зависеть от формы, в которой MuPAD возвращает результаты. Например, если вы задаете тип следующего обыкновенного дифференциального уравнения как Chini, решатель возвращает три разных решения:
o:= ode(y'(x) = x*y(x)^2 + x*y(x) + x, y(x)): L:= solve(o, Type = Chini)
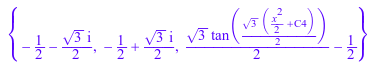
При определении типа того же обыкновенного дифференциального уравнения, когда Riccati дает вам два разных решения:
M := solve(o, Type = Riccati)
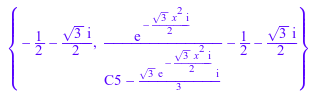
Когда вы задаете тип уравнения как Riccati, решатель возвращает более общий результат. Этот результат комбинирует вторые и третьи элементы набора, возвращенного для типа Chini. Дополнительное решение для уравнения Chini появляется в особом значении интегрирования, постоянного для уравнения Riccati. Найдите значение константы, в которой более общее решение для уравнения Riccati обращается к второму решению для уравнения Chini:
solve(L[2] = M[2], C5)
![]()
Используйте evalAt чтобы проверить, что, если постоянное интегрирование 0, решение для уравнения Riccati дает дополнительное решение, что вы видите тип Chini:
evalAt(M[2], C5 = 0)
![]()
Можно найти зависимость между константами в решениях возвращенной для типов Riccati и Chini. Как первый шаг, перепишите результаты, использующие подобные термины. Например, перепишите выражение с экспонентами в терминах касательных:
m2 := rewrite(M[2], tan)
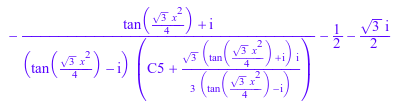
Задайте постоянный C5 в терминах C4:
C5 := simplify(solve(L[3] = m2, C5, IgnoreSpecialCases))
![]()
Теперь, если вы хотите проверить, что две формы решения эквивалентны, заменяют константой в решении Riccati с этим выражением.
Для получения дополнительной информации о тестировании математической эквивалентности решений смотрите Результаты Тестирования.
Возвращенные результаты могут отличаться от того, что вы ожидали из-за неполноты ожидаемого или возвращенного набора решения. Полные наборы решений составляют все особые случаи для всех символьных параметров и переменных, включенных в уравнение. Полные решения могут быть очень большими и сложными. Часто вам нужно только одно практическое решение от длинного или бесконечного набора решения. Некоторые решатели спроектированы, чтобы возвратить неполные, но практические решения. Например, считайте уравнение a x + b = y. При решении этого уравнения в Командном окне MATLAB® тулбокс игнорирует особые регистры:
>> решают ('a*x + b = y')
ans =
- (b - y)/a
MuPAD возвращает полный набор решений, составляющих все возможные значения символьных параметров aB, и y:
solve(a*x + b = y, x)
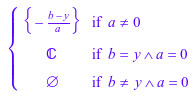
Решение уравнения в MuPAD с IgnoreSpecialCases опция, вы получаете тот же короткий результат как в Окне Команды MATLAB:
solve(a*x + b = y, x, IgnoreSpecialCases)
![]()
Некоторые уравнения имеют бесконечное число решений. При решении того же уравнения в Окне Команды MATLAB вы получаете только одно решение от бесконечного множества:
>> syms x;
>> решают (sin (x))
ans =
0
По умолчанию решатель MuPAD возвращает все решения:
S := solve(sin(x), x)
![]()
Чтобы получить один элемент набора решения, используйте solvelib::getElement команда:
solvelib::getElement(S)
![]()
Если вы хотите, чтобы решатель возвратил всего одно решение, используйте PrincipalValue опция:
S := solve(sin(x), x, PrincipalValue)
![]()
PrincipalValue может помочь вам сократить результаты, не использующие все решения, кроме одного. Опция не позволяет вам выбирать конкретное решение.