Документация

Одномерная нелинейная регрессия

Нелинейная регрессия может принять любой тип отношения между зависимой переменной y и независимыми переменными x _j. Для нелинейной регрессии MuPAD^® обеспечивает stats::reg функция. Эта функция использует подход наименьших квадратов в вычислении регрессии. stats::reg выбирает параметры p ₁, ..., p _n путем попытки минимизировать квадратичную ошибку:

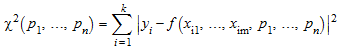Здесь x _ij является iизмерение th независимой переменной x _j. stats::reg функция также может выполнить метод взвешенных наименьших квадратов нелинейная регрессия. По умолчанию веса равны 1.

stats::reg возвращает список оптимизированных параметров [p ₁, ..., p _n] и минимизированное значение квадратичной ошибки для заданной модели. Предположим, вы хотите найти модель для следующих данных:

sampleX := [1, 2, 3, 4, 5, 6, 7, 8, 9]:
sampleY := [36.97666099, 54.14911101, 131.3852077,
            30.43939553, 202.2004454, 129.5801972,
            321.0663718, 411.3959961, 929.597986]:

Отображение на графике данных может помочь вам выбрать модель:

plot1 := plot::Scatterplot(sampleX, sampleY,
                      LinesVisible = FALSE):
plot(plot1)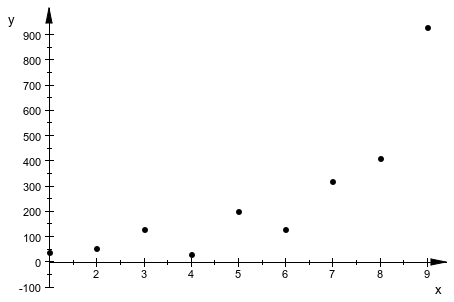

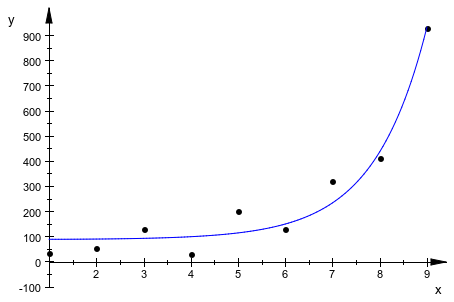
График рассеивания ясно показывает, что линейные модели не соответствуют данным. Зависимость выглядит похожей на экспоненциал. Поэтому можно попытаться соответствовать данным к различным моделям, включающим показательные функции. Предположим, вы хотите попробовать подгонку данных к выражению:

fit := stats::reg(sampleX, sampleY, p1 + p2^2*exp(x1)/x1,
                                          [x1], [p1, p2])

stats::reg функция возвращает параметры модели и квадратичной ошибки как вложенный список. Чтобы получить доступ к параметрам отдельно, используйте следующие команды:

a := fit[1][1];
b := fit[1][2];
chi2 := fit[2]

Теперь отобразите на графике данные и выражение, что вы раньше соответствовали данным по тому же графику. Этот график показывает, как выражение модели соответствует данным:

plot2 := plot::Function2d(a + b^2*exp(x)/x, x = 1..9):
plot(plot1, plot2)