Документация

Создайте временные предположения

Используйте временные предположения, чтобы указать, что объект содержит математические свойства для конкретного вычисления. Временные предположения также помогают вам сузить общее решение и получить определенные решения. Например, следующее уравнение описывает линейное движение с постоянным ускорением:. здесь, r расстояние объектные перемещения, r ₀ является начальным расстоянием, v ₀ является начальной скоростью, a постоянное ускорение и t время перемещения. Если вы знаете все другие параметры и хотите вычислить время, когда объект перемещался, решите уравнение для переменной t:

t = solve(r = r_0 + v_0*t + a*t^2/2, t)

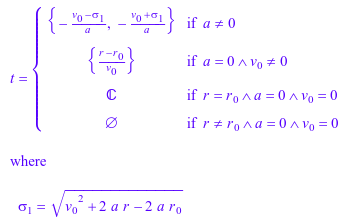
Предположим, вы хотите сохранить общее решение для всех возможных случаев линейного движения с постоянным ускорением. Вы также хотите вывести несколько особых случаев этого движения и получить конкретные решения для этих случаев. Например, один из объектов вы рассматриваете перемещения с постоянной скоростью. Выведите решение для этого объекта из общего решения в течение времени движения путем принятия ускорения a = 0:

t = solve(r = r_0 + v_0*t + a*t^2/2, t)
    assuming a = 0 and r > r_0 and v_0 > 0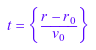

Предположение a = 0 сохраняется только для этого конкретного вызова solve. Предположение не влияет на другие вычисления:

is(a = 0)

Если вы устанавливаете предположение в форме неравенства, обе стороны неравенства должны представлять действительные значения. Неравенства с комплексными числами недопустимы, потому что поле комплексных чисел не является упорядоченным полем. Например, при попытке использовать следующее предположение, MuPAD^® возвращает ошибку:

y + 1 assuming y > 2*I

Error: Inconsistent assumptions. [property::_assume]

Можно использовать комплексные числа в предположениях, представленных в формах уравнений:

y + 1 assuming y = 2*I

Присвойте временные ценности параметрам

Чтобы решить линейное уравнение движения для особых значений параметров, присвойте значения параметрам:

r := 4:
r_0 := 0:
v_0 := 3:
a := 2:
t = solve(r = r_0 + v_0*t + a*t^2/2, t) assuming t > 0

Если вы используете присвоения, MuPAD оценивает переменные к их значениям во всех дальнейших расчетах:

r, r_0, v_0, a

Чтобы смочь снова использовать переменные в дальнейших расчетах, используйте delete команда:

delete r, r_0, v_0, a

Используя предположения, можно временно присвоить значения параметрам. Например, решите уравнение для следующих значений:

t = solve(r = r_0 + v_0*t + a*t^2/2, t)
assuming r = 4 and r_0 = 0 and v_0 = 3 and a = 2 and t > 0

Переменные остаются свободными для дальнейших вычислений, потому что временные предположения не сохраняются:

r, r_0, v_0, a, t

Если предположения содержат линейные уравнения с одной переменной, MuPAD решает эти уравнения, вставляет решения в выражение, и затем выполняет выражение:

r = r_0 + v_0*t + a*t^2/2 assuming  a + 5 = 5
                          and 2*v_0 + 4 = 14
                          and t = 3 and r_0 = 0

Взаимодействия между временными и постоянными предположениями

assuming команда временно перезаписывает весь постоянный набор предположений на объекте:

assume(z in R_);
z assuming z = -2*I

После оценки оператора с временным предположением MuPAD восстанавливает постоянное предположение:

is(z in R_)

Смотрите, как использовать временные предположения в сочетании с постоянными предположениями в Использовании Временных Предположений сверх Постоянных Предположений.

Используйте временные предположения сверх постоянных предположений

Предположим, что вы устанавливаете постоянные предположения на объекте MuPAD. Если вы оцениваете объект с временным предположением, установленным assuming команда, MuPAD игнорирует постоянные предположения в этой оценке:

assume(x in R_);
solve(x^3 + x = 0, x) assuming (x <> 0)

Чтобы использовать постоянные предположения и временное предположение вместе, добавьте временное предположение с помощью assumingAlso команда:

assume(x in R_);
solve(x^3 + x = 0, x) assumingAlso (x <> 0)

Когда вы используете временные предположения сверху постоянных единиц, всегда проверяйте, что предположения не противоречат друг другу. Противоречие предположениям может привести к противоречивым и непредсказуемым результатам. В некоторых случаях MuPAD обнаруживает конфликтные предположения и выпускает следующую ошибку:

assume(x < 0);
x assumingAlso (x > 0);

Error: Inconsistent assumptions. [property::_assume]

MuPAD не гарантирует, что обнаружил предположения противоречия:

assume(x, Type::Even);
x assumingAlso (x + 1, Type::Even)