Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Z-преобразование функционального F(z) определяется следующим образом:
Если R положительное число, такое что функциональный F(Z) аналитично на и вне кругового |z| = R, затем обратное Z-преобразование определяется следующим образом:
Можно рассмотреть Z-преобразование как дискретный эквивалент Преобразования Лапласа.
Чтобы вычислить Z-преобразование арифметического выражения, используйте ztrans функция. Например, вычислите Z-преобразование следующего выражения:
S := ztrans(sinh(n), n, z)
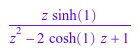
Если вы знаете Z-преобразование выражения, можно найти исходное выражение или математически эквивалентную форму путем вычисления обратного Z-преобразования. Чтобы вычислить обратное Z-преобразование, используйте iztrans функция. Например, вычислите обратное Z-преобразование выражения S:
iztrans(S, z, n)
![]()
Предположим, вы вычисляете Z-преобразование выражения, и затем вычисляете обратное Z-преобразование результата. В этом случае MuPAD® может возвратить выражение, которое математически эквивалентно исходному, но представленное в другой форме. Например, вычислите Z-преобразование следующего выражения:
C := ztrans(exp(n), n, z)
![]()
Теперь вычислите обратное Z-преобразование получившегося выражения C. Результат отличается от исходного выражения:
invC := iztrans(C, z, n)
![]()
Упрощение получившегося выражения invC дает исходное выражение:
simplify(invC)
![]()
Помимо арифметических выражений, ztrans и iztrans функции также принимают матрицы арифметических выражений. Например, вычислите Z-преобразование следующей матрицы:
A := matrix(2, 2, [1, n, n + 1, 2*n + 1]): ZA := ztrans(A, n, z)
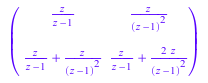
Вычисление обратного Z-преобразования ZA дает исходный матричный A:
iztrans(ZA, z, n)
![]()
ztrans и iztrans функции позволяют вам оценить преобразования выражения или матрицы в конкретной точке. Например, оцените Z-преобразование следующего выражения для значения z = 2:
ztrans(1/n!, n, 2)
![]()
Оцените обратное Z-преобразование следующего выражения для значения n = 10:
iztrans(z/(z - exp(x)), z, 10)
![]()
Если MuPAD не может вычислить Z-преобразование или обратное Z-преобразование выражения, это возвращается, неразрешенный преобразуйте:
ztrans(f(n), n, z)
![]()
iztrans(F(z), z, n)
![]()