ldaModel

Модель Latent Dirichlet allocation (LDA)

Описание

Модель скрытого выделения Дирихле (LDA) является моделью темы, которая обнаруживает базовые темы в наборе документов и выводит вероятности слова в темах. Если модель была подходящим использованием мешка n модели граммов, то программное обеспечение обрабатывает N-граммы как отдельные слова.

Создание

Создайте модель LDA с помощью fitlda функция.

Свойства

развернуть все

`NumTopics` — Количество тем
положительное целое число

Количество тем в модели LDA, заданной как положительное целое число.

`TopicConcentration` — Концентрация темы
положительная скалярная величина

Концентрация темы, заданная как положительная скалярная величина. Функция устанавливает концентрацию на тему к TopicConcentration/NumTopics. Для получения дополнительной информации смотрите Скрытое Выделение Дирихле.

`WordConcentration` — Концентрация Word
1 (значение по умолчанию) | неотрицательный скаляр

Концентрация Word, заданная как неотрицательный скаляр. Программное обеспечение устанавливает концентрацию на слово к WordConcentration/numWords, где numWords размер словаря входных документов. Для получения дополнительной информации смотрите Скрытое Выделение Дирихле.

`CorpusTopicProbabilities` — Вероятности темы входного документа установлены
вектор

Вероятности темы входного набора документа, заданного как вектор. Корпусные вероятности темы модели LDA являются вероятностями наблюдения, что каждая тема в целом наборе данных раньше подбирала модель LDA. CorpusTopicProbabilities 1 K вектором, где K является количеством тем. k th запись CorpusTopicProbabilities соответствует вероятности наблюдения темы k.

`DocumentTopicProbabilities` — Вероятности темы на входной документ
матрица

Вероятности темы на входной документ, заданный как матрица. Вероятности тематики документа модели LDA являются вероятностями наблюдения, что каждая тема в каждом документе раньше подбирала модель LDA. DocumentTopicProbabilities D-by-K матрица, где D является количеством документов, используемых, чтобы подбирать модель LDA, и K является количеством тем. (d,k) th запись DocumentTopicProbabilities соответствует вероятности наблюдения темы k в документе d.

Если у кого-либо темы есть нулевая вероятность (CorpusTopicProbabilities содержит нули), затем соответствующие столбцы DocumentTopicProbabilities и TopicWordProbabilities нули.

Порядок строк в DocumentTopicProbabilities соответствует порядку документов в обучающих данных.

`TopicWordProbabilities` — Вероятности Word на тему
матрица

Вероятности Word на тему, заданную как матрица. Вероятности слова темы модели LDA являются вероятностями наблюдения каждого слова в каждой теме модели LDA. TopicWordProbabilities V-by-K матрица, где V является количеством слов в Vocabulary и K является количеством тем. (v,k) th запись TopicWordProbabilities соответствует вероятности наблюдения слова v в теме k.

Порядок строк в TopicWordProbabilities соответствует порядку слов в Vocabulary.

`TopicOrder` — Порядок темы
`'initial-fit-probability'` (значение по умолчанию) | `'unordered'`

Порядок темы, заданный как одно из следующего:

'initial-fit-probability' – Сортировка тем корпусными вероятностями темы начальной подгонки модели. Этими вероятностями является CorpusTopicProbabilities свойство начального ldaModel объект возвращен fitlda. resume функция не переупорядочивает темы получившегося ldaModel объекты.
'unordered' – Не заказывайте темы.

`FitInfo` — Информация зарегистрирована, подбирая модель LDA
struct ()

Информация зарегистрирована, подбирая модель LDA, заданную как struct со следующими полями:

TerminationCode – Состояние оптимизации на выход
- 0 – Предел итерации достигнут.
- 1 – Допуск на логарифмической правдоподобности, которой удовлетворяют.
TerminationStatus – Объяснение возвращенного кода завершения
NumIterations – Количество итераций выполняется
NegativeLogLikelihood – Отрицательная логарифмическая правдоподобность для данных передала fitlda
Perplexity – Недоумение для данных передало fitlda
Solver – Имя решателя используется
History – Struct, содержащий историю оптимизации
StochasticInfo – Информация содержащего Struct для стохастических решателей

Типы данных: struct

`Vocabulary` — Список слов в модели
вектор строки

Список слов в модели, заданной как вектор строки.

Типы данных: string

Функции объекта

`logp`	Логарифмические вероятности документа и качество подгонки модели LDA
`predict`	Предскажите главные темы LDA документов
`resume`	Продолжите подбирать модель LDA
`topkwords`	Большинство важных слов в модели сумки слов или теме LDA
`transform`	Преобразуйте документы в более низкое мерное пространство
`wordcloud`	Создайте график облака слова из текста, модели сумки слов, мешка n модели граммов или модели LDA

Примеры

свернуть все

Подбирайте модель LDA

Скрипт Open Live Script

Чтобы воспроизвести результаты в этом примере, установите rng к 'default'.

rng('default')

Загрузите данные в качестве примера. Файл sonnetsPreprocessed.txt содержит предварительно обработанные версии сонетов Шекспира. Файл содержит один сонет на строку со словами, разделенными пробелом. Извлеките текст из sonnetsPreprocessed.txt, разделите текст в документы в символах новой строки, и затем маркируйте документы.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель сумки слов использование bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Подбирайте модель LDA с четырьмя темами.

numTopics = 4;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.107614 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.03 |            |  1.215e+03 |         1.000 |             0 |
|          1 |       0.04 | 1.0482e-02 |  1.128e+03 |         1.000 |             0 |
|          2 |       0.01 | 1.7190e-03 |  1.115e+03 |         1.000 |             0 |
|          3 |       0.02 | 4.3796e-04 |  1.118e+03 |         1.000 |             0 |
|          4 |       0.02 | 9.4193e-04 |  1.111e+03 |         1.000 |             0 |
|          5 |       0.02 | 3.7079e-04 |  1.108e+03 |         1.000 |             0 |
|          6 |       0.02 | 9.5777e-05 |  1.107e+03 |         1.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 4
             WordConcentration: 1
            TopicConcentration: 1
      CorpusTopicProbabilities: [0.2500 0.2500 0.2500 0.2500]
    DocumentTopicProbabilities: [154x4 double]
        TopicWordProbabilities: [3092x4 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Визуализируйте темы с помощью облаков слова.

figure
for topicIdx = 1:4
    subplot(2,2,topicIdx)
    wordcloud(mdl,topicIdx);
    title("Topic: " + topicIdx)
end

Самые высокие слова вероятности темы LDA

Скрипт Open Live Script

Составьте таблицу слов с самой высокой вероятностью темы LDA.

Чтобы воспроизвести результаты, установите rng к 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель сумки слов использование bagOfWords.

bag = bagOfWords(documents);

Подбирайте модель LDA с 20 темами. Чтобы подавить многословный выход, установите 'Verbose' к 0.

numTopics = 20;
mdl = fitlda(bag,numTopics,'Verbose',0);

Найдите лучшие 20 слов первой темы.

k = 20;
topicIdx = 1;
tbl = topkwords(mdl,k,topicIdx)

tbl=20×2 table
      Word        Score  
    ________    _________

    "eyes"        0.11155
    "beauty"      0.05777
    "hath"       0.055778
    "still"      0.049801
    "true"       0.043825
    "mine"       0.033865
    "find"       0.031873
    "black"      0.025897
    "look"       0.023905
    "tis"        0.023905
    "kind"       0.021913
    "seen"       0.021913
    "found"      0.017929
    "sin"        0.015937
    "three"      0.013945
    "golden"    0.0099608
      ⋮

Найдите лучшие 20 слов первой темы и используйте среднее значение инверсии масштабироваться на баллах.

tbl = topkwords(mdl,k,topicIdx,'Scaling','inversemean')

tbl=20×2 table
      Word       Score  
    ________    ________

    "eyes"        1.2718
    "beauty"     0.59022
    "hath"        0.5692
    "still"      0.50269
    "true"       0.43719
    "mine"       0.32764
    "find"       0.32544
    "black"      0.25931
    "tis"        0.23755
    "look"       0.22519
    "kind"       0.21594
    "seen"       0.21594
    "found"      0.17326
    "sin"        0.15223
    "three"      0.13143
    "golden"    0.090698
      ⋮

Создайте облако слова с помощью масштабированных баллов в качестве данных о размере.

figure
wordcloud(tbl.Word,tbl.Score);

Вероятности тематики документа модели LDA

Скрипт Open Live Script

Доберитесь вероятности тематики документа (также известный как смеси темы) документов раньше подбирали модель LDA.

Чтобы воспроизвести результаты, установите rng к 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель сумки слов использование bagOfWords.

bag = bagOfWords(documents);

Подбирайте модель LDA с 20 темами. Чтобы подавить многословный выход, установите 'Verbose' к 0.

numTopics = 20;
mdl = fitlda(bag,numTopics,'Verbose',0)

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [1x20 double]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Просмотрите вероятности темы первого документа в обучающих данных.

topicMixtures = mdl.DocumentTopicProbabilities;
figure
bar(topicMixtures(1,:))
title("Document 1 Topic Probabilities")
xlabel("Topic Index")
ylabel("Probability")

Предскажите главные темы LDA документов

Скрипт Open Live Script

Чтобы воспроизвести результаты в этом примере, установите rng к 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель сумки слов использование bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Подбирайте модель LDA с 20 темами.

numTopics = 20;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.172684 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.18 |            |  1.159e+03 |         5.000 |             0 |
|          1 |       0.10 | 5.4884e-02 |  8.028e+02 |         5.000 |             0 |
|          2 |       0.06 | 4.7400e-03 |  7.778e+02 |         5.000 |             0 |
|          3 |       0.09 | 3.4597e-03 |  7.602e+02 |         5.000 |             0 |
|          4 |       0.07 | 3.4662e-03 |  7.430e+02 |         5.000 |             0 |
|          5 |       0.08 | 2.9259e-03 |  7.288e+02 |         5.000 |             0 |
|          6 |       0.05 | 6.4180e-05 |  7.291e+02 |         5.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [1x20 double]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Предскажите главные темы для массива новых документов.

newDocuments = tokenizedDocument([
    "what's in a name? a rose by any other name would smell as sweet."
    "if music be the food of love, play on."]);
topicIdx = predict(mdl,newDocuments)

topicIdx = 2×1

    19
     8

Визуализируйте предсказанные темы с помощью облаков слова.

figure
subplot(1,2,1)
wordcloud(mdl,topicIdx(1));
title("Topic " + topicIdx(1))
subplot(1,2,2)
wordcloud(mdl,topicIdx(2));
title("Topic " + topicIdx(2))

Больше о

развернуть все

Скрытое выделение Дирихле

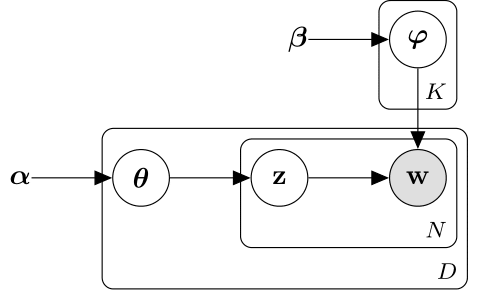
Модель скрытого выделения Дирихле (LDA) является моделью тематики документа, которая обнаруживает базовые темы в наборе документов и выводит вероятности слова в темах. LDA моделирует набор документов D как смеси темы $θ_{1}, \dots, θ_{D}$ , по темам K, охарактеризованным векторами вероятностей слова $φ_{1}, \dots, φ_{K}$ . В модели принимается, что смеси темы $θ_{1}, \dots, θ_{D}$ , и темы $φ_{1}, \dots, φ_{K}$ следуйте за распределением Дирихле параметрами концентрации $α$ и $β$ соответственно.

Смеси темы $θ_{1}, \dots, θ_{D}$ векторы вероятности длины K, где K является количеством тем. Запись $θ_{d i}$ вероятность темы i, появляющийся в d th документ. Смеси темы соответствуют строкам DocumentTopicProbabilities свойство ldaModel объект.

Темы $φ_{1}, \dots, φ_{K}$ векторы вероятности длины V, где V является количеством слов в словаре. Запись $φ_{i v}$ соответствует вероятности v th слово словаря, появляющегося в i th тема. Темы $φ_{1}, \dots, φ_{K}$ соответствуйте столбцам TopicWordProbabilities свойство ldaModel объект.

Учитывая темы $φ_{1}, \dots, φ_{K}$ и предшествующий Дирихле $α$ на смесях темы LDA принимает следующий порождающий процесс для документа:

Произведите смесь темы $θ ~ Дирихле (α)$ . Случайная переменная $θ$ вектор вероятности длины K, где K является количеством тем.
Для каждого слова в документе:
1. Произведите список тем $z ~ Категориальный (θ)$ . z случайной переменной является целым числом от 1 до K, где K является количеством тем.
2. Произведите слово $w ~ Категориальный (φ_{z})$ . w случайной переменной является целым числом от 1 до V, где V является количеством слов в словаре и представляет соответствующее слово в словаре.

При этом порождающем процессе, совместном распределении документа со словами $w_{1}, \dots, w_{N}$ , со смесью темы $θ$ , и с индексами темы $z_{1}, \dots, z_{N}$ дают

$p (θ, z, w | α, φ) = p (θ | α) \prod_{n = 1}^{N} p (z_{n} | θ) p (w_{n} | z_{n}, φ),$

где N является количеством слов в документе. Подведение итогов совместного распределения по z и затем интеграция $θ$ дает к предельному распределению документа w:

$p (w | α, φ) = \int_{θ} p (θ | α) \prod_{n = 1}^{N} \sum_{z_{n}} p (z_{n} | θ) p (w_{n} | z_{n}, φ) d θ .$

Следующая схема иллюстрирует модель LDA как вероятностную графическую модель. Теневые узлы являются наблюдаемыми переменными, незаштрихованные узлы являются скрытыми переменными, узлы без основ являются параметрами модели. Стрелы подсвечивают, что зависимости между случайными переменными и пластинами указывают на повторенные узлы.

Распределение Дирихле

Распределение Дирихле является непрерывным обобщением распределения многочлена. Учитывая количество категорий $K \geq 2$ , и параметр концентрации $α$ , где $α$ вектор положительных реалов длины K, функцией плотности вероятности распределения Дирихле дают

$p (θ ∣ α) = \frac{1}{B (α)} \prod_{i = 1}^{K} θ_{i}^{α_{i} - 1},$

где B обозначает многомерную Бета-функцию, данную

$B (α) = \frac{\prod_{i = 1}^{K} Γ (α_{i})}{Γ (\sum_{i = 1}^{K} α_{i})} .$

Особый случай распределения Дирихле является симметричным распределением Дирихле. Симметричное распределение Дирихле характеризуется параметром концентрации $α$ , где все элементы $α$ то же самое.

Документация

ldaModel

Описание

Создание

Свойства

`NumTopics` — Количество тем
положительное целое число

`TopicConcentration` — Концентрация темы
положительная скалярная величина

`WordConcentration` — Концентрация Word
1 (значение по умолчанию) | неотрицательный скаляр

`CorpusTopicProbabilities` — Вероятности темы входного документа установлены
вектор

`DocumentTopicProbabilities` — Вероятности темы на входной документ
матрица

`TopicWordProbabilities` — Вероятности Word на тему
матрица

`TopicOrder` — Порядок темы
`'initial-fit-probability'` (значение по умолчанию) | `'unordered'`

`FitInfo` — Информация зарегистрирована, подбирая модель LDA
struct ()

`Vocabulary` — Список слов в модели
вектор строки

Функции объекта

Примеры

Подбирайте модель LDA

Самые высокие слова вероятности темы LDA

Вероятности тематики документа модели LDA

Предскажите главные темы LDA документов

Больше о

Скрытое выделение Дирихле

Распределение Дирихле

Смотрите также

Темы

Введенный в R2017b

Документация Text Analytics Toolbox

Поддержка

Документация

ldaModel

Описание

Создание

Свойства

NumTopics — Количество тем положительное целое число

TopicConcentration — Концентрация темы положительная скалярная величина

WordConcentration — Концентрация Word1 (значение по умолчанию) | неотрицательный скаляр

CorpusTopicProbabilities — Вероятности темы входного документа установлены вектор

DocumentTopicProbabilities — Вероятности темы на входной документ матрица

TopicWordProbabilities — Вероятности Word на тему матрица

TopicOrder — Порядок темы 'initial-fit-probability' (значение по умолчанию) | 'unordered'

FitInfo — Информация зарегистрирована, подбирая модель LDA struct ()

Vocabulary — Список слов в модели вектор строки

Функции объекта

Примеры

Подбирайте модель LDA

Самые высокие слова вероятности темы LDA

Вероятности тематики документа модели LDA

Предскажите главные темы LDA документов

Больше о

Скрытое выделение Дирихле

Распределение Дирихле

Смотрите также

Темы

Введенный в R2017b

Документация Text Analytics Toolbox

Поддержка

`NumTopics` — Количество тем
положительное целое число

`TopicConcentration` — Концентрация темы
положительная скалярная величина

`WordConcentration` — Концентрация Word
1 (значение по умолчанию) | неотрицательный скаляр

`CorpusTopicProbabilities` — Вероятности темы входного документа установлены
вектор

`DocumentTopicProbabilities` — Вероятности темы на входной документ
матрица

`TopicWordProbabilities` — Вероятности Word на тему
матрица

`TopicOrder` — Порядок темы
`'initial-fit-probability'` (значение по умолчанию) | `'unordered'`

`FitInfo` — Информация зарегистрирована, подбирая модель LDA
struct ()

`Vocabulary` — Список слов в модели
вектор строки