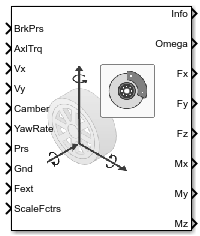
Combined Slip Wheel 2DOF

Объединенный промах 2DOF колесо с диском, барабаном или сопоставленным тормозом

Библиотека:
Vehicle Dynamics Blockset / Колеса и Шины

Описание

Блок Combined Slip Wheel 2DOF реализует продольное и боковое поведение колеса, охарактеризованного Волшебной ^{Формулой [1] и [2]}. Используйте блок в автомобильной трансмиссии и симуляциях транспортного средства, где низкочастотная дорога шины и тормозные усилия обязаны определять ускорение транспортного средства, торможение и сопротивление качению колеса. Блок подходит для приложений, которые требуют объединенного бокового промаха, например, в боковом движении и исследованиях устойчивости отклонения от курса.

На основе крутящего момента автомобильной трансмиссии, тормозного давления, дорожной высоты, угла изгиба колеса и давления инфляции, блок определяет уровень вращения колеса, вертикальное движение, силы, и моменты во всех шести степенях свободы (DOF). Используйте вертикальную степень свободы, чтобы изучить резонансы приостановки шины от дорожных профилей или движения шасси.

Чтобы реализовать Волшебную Формулу, блок использует эмпирические уравнения ^{[1] и [2]}. Подходящие коэффициенты использования уравнений, которые соответствуют параметрам блоков.

Обновить параметры блоков с подходящими коэффициентами из файла:

На Wheel and Tire Parameters> панель Tire, выберите Select file.
Выберите содействующий файл шины.
Выберите Apply.
Выберите Update mask values from file. В диалоговом окне, которое предлагает вам подтверждение, нажмите OK. Блок обновляет параметры.

Используйте параметр Brake Type, чтобы выбрать тормоз.

Тормозите установку типа	Тормозите реализацию
`None`	'none'
`Disc`	Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие
`Drum`	Симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной момент
`Mapped`	Интерполяционная таблица, которая является функцией скорости колеса и примененного тормозного давления

Вращательная динамика колеса

Блок вычисляет инерционный ответ колеса, удовлетворяющего:

Потери оси
Тормозите и управляйте крутящим моментом
Утомите сопротивление качению
Оснуйте контакт через дорожный шиной интерфейс

Чтобы реализовать Волшебную Формулу, блок использует эти уравнения.

Вычисление	Уравнения
Продольная сила	Шина и Динамика аппарата ^[2] уравнения 4. E9 до 4. E57
Боковая сила - чистый занос	Шина и Динамика аппарата ^[2] уравнения 4. E19 до 4. E30
Боковая сила - объединенный промах	Шина и Динамика аппарата ^[2] уравнения 4. E58 до 4. E67
Вертикальная динамика	Шина и Динамика аппарата ^[2] уравнения 4. E68, 4. E1, 4. E2a, и 4. 2 миллиарда евро
Опрокидывание пары	Шина и Динамика аппарата ^[2] уравнение 4. E69
Сопротивление качению	Улучшенная Волшебная модель шины Формулы / Свифта, которая может обработать скачки давления инфляции ^[1] уравнение 6.1.2 Шина и Динамика аппарата ^[2] уравнение 4. E70
Выравнивание момента	Шина и Динамика аппарата ^[2] уравнение 4. E31 до 4. E49
Выравнивание крутящего момента - объединенный промах	Шина и Динамика аппарата ^[2] уравнение 4. E71 до 4. E78

Входной крутящий момент является суммированием прикладного крутящего момента оси, тормозного момента, и момент, являющийся результатом объединенного крутящего момента шины.

$T_{i} = T_{a} - T_{b} + T_{d}$

В настоящий момент являясь результатом объединенного крутящего момента шины, блок реализует тяговые силы колеса и сопротивление качению с динамикой первого порядка. Сопротивлению качению параметризовали постоянную времени в терминах релаксационной длины.

$T_{d} (s) = \frac{1}{\frac{| ω | R_{e}}{L_{e}} s + 1} (F_{x} R_{e} + M_{y})$

Если тормоза включены, блок определяет торможение заблокированное или разблокированное условие на основе идеализированной сухой модели трения муфты. На основе условия тупика блок реализует их трение и динамические модели.

Если	Условие тупика	Модель трения	Динамическая модель
$\begin{array}{l} ω \neq \\ 0or \\ T_{S} < \| T_{i} + T_{f} - ω b \| \end{array}$	Разблокированный	$\begin{array}{l} T_{f} = T_{k} \\ где, \\ T_{k} = F_{c} R_{e f f} μ_{k} \tanh [4 (- ω_{d})] \\ T_{s} = F_{c} R_{e f f} μ_{s} \\ R_{e f f} = \frac{2 (R_{o}^{3} - R_{i}^{3})}{3 (R_{o}^{2} - R_{i}^{2})} \end{array}$	$\dot{ω} J = - ω b + T_{i} + T_{o}$
$\begin{array}{l} ω = \\ 0and \\ T_{S} \geq \| T_{i} + T_{f} - ω b \| \end{array}$	Заблокированный	$T_{f} = T_{s}$	$ω = 0$

Уравнения используют эти переменные.

ω	Скорость вращения колеса
a	Скорость независимый компонент силы
b	Линейный скоростной компонент силы
c	Квадратичный скоростной компонент силы
_Le	Утомите релаксационную длину
J	Момент инерции
_My	Крутящий момент сопротивления качению
_Ta	Прикладной крутящий момент оси об оси вращения колеса
_Tb	Тормозной момент
_Td	Объединенный крутящий момент шины
_Tf	Фрикционный крутящий момент
_Ti	Сетевой входной крутящий момент
_Tk	Кинетический фрикционный крутящий момент
_To	Сетевой выходной крутящий момент
_Ts	Статический фрикционный крутящий момент
_Fc	Прикладывавшая сила муфты
_Fx	Продольная сила, разработанная дорогой шины, взаимодействует через интерфейс должный уменьшиться
_Reff	Эффективный радиус муфты
_Ro	Кольцевой диск внешний радиус
_Ri	Кольцевой диск внутренний радиус
_Re	Эффективный радиус шины, в то время как при загрузке и при данном давлении
_Vx	Продольная скорость оси
_Fz	Транспортное средство нормальная сила
ɑ	Экспонента давления воздуха в шине
β	Нормальная экспонента силы
_pi	Давление воздуха в шине
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения

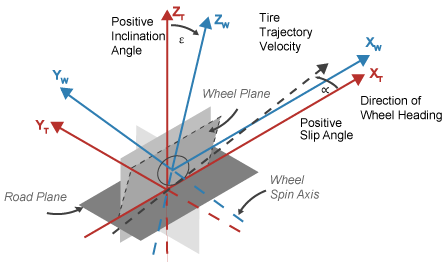
Шина и системы координат колеса

Чтобы разрешить силы и моменты, блок использует ориентацию Z-Up систем координат шины и колеса.

Утомите оси системы координат (_XT, _YT, _ZT) фиксируются в системе координат, присоединенной к шине. Источник в контакте шины с землей.
Оси системы координат колеса (_XW, _YW, _ZW) фиксируются в системе координат, присоединенной к колесу. Источник стоит у руля центр.

Ориентация Z-Up ^[1]

Тормоза

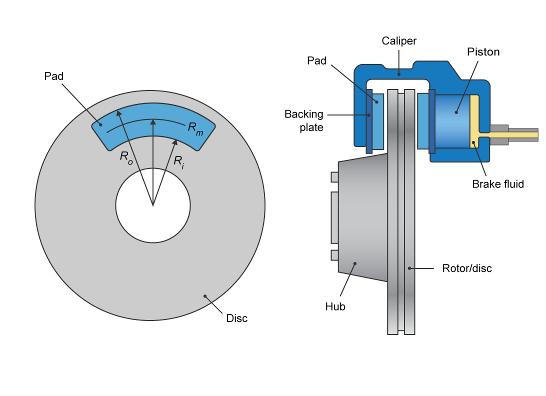
Диск

Если вы задаете параметр Brake Type Disc, блок реализует дисковый тормоз. Этот рисунок показывает виды сбоку и виды спереди дискового тормоза.

Дисковый тормоз преобразует давление в тормозном цилиндре от тормозного цилиндра в силу. Дисковый тормоз прикладывает силу в среднем радиусе тормозной колодки.

Блок использует эти уравнения, чтобы вычислить момент привода для дискового тормоза.

$T = {\begin{matrix} \frac{μ P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N \neq 0 \\ \frac{μ_{s t a t i c} P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N = 0 \end{matrix}$

$R m = \frac{R o + R i}{2}$

Уравнения используют эти переменные.

T	Момент привода
P	Прикладное тормозное давление
N	Скорость колеса
_Npads	Количество тормозных колодок в блоке дискового тормоза
_μstatic	Коэффициент ротора клавиатуры диска статического трения
μ	Коэффициент ротора клавиатуры диска кинетического трения
_Ba	Тормозите внутренний диаметр привода
_Rm	Средний радиус тормозной колодки обеспечивает приложение на тормозном роторе
_Ro	Внешний радиус тормозной колодки
_Ri	Внутренний радиус тормозной колодки

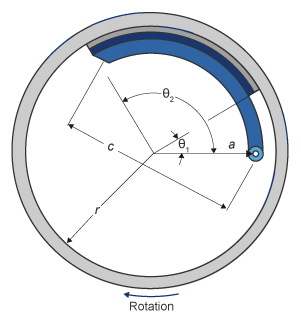
Барабан

Если вы задаете параметр Brake Type Drum, блок реализует статический (установившийся) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двухстороннего гидравлического привода и двух тормозных колодок. Тормозные колодки не совместно используют общий контакт стержня.

Симплексная модель барабанного тормоза использует приложенную силу и геометрию тормоза, чтобы вычислить крутящий момент привода для каждой тормозной колодки. Модель барабана принимает, что приводы и геометрия обуви симметричны для обеих сторон, позволяя одному набору геометрии и параметров трения использоваться в обоих ботинках.

Блок реализует уравнения, которые выведены из этих уравнений в Основных принципах Элементов Машины.

$\begin{array}{l} T_{r s h o e} = (\frac{π μ c r (потому что θ_{2} - потому что θ_{1}) B_{a}^{2}}{2 μ (2 r (потому что θ_{2} - потому что θ_{1}) + a ({потому что}^{2} θ_{2} - {потому что}^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \\ T_{l s h o e} = (\frac{π μ c r (потому что θ_{2} - потому что θ_{1}) B_{a}^{2}}{- 2 μ (2 r (потому что θ_{2} - потому что θ_{1}) + a ({потому что}^{2} θ_{2} - {потому что}^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \end{array}$

$T = {\begin{matrix} T_{r s h o e} + T_{l s h o e} когда N \neq 0 \\ (T_{r s h o e} + T_{l s h o e}) \frac{μ_{s t a t i c}}{μ} когда N = 0 \end{matrix}$

Уравнения используют эти переменные.

T	Момент привода
P	Прикладное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент ротора клавиатуры диска статического трения
μ	Коэффициент ротора клавиатуры диска кинетического трения
_Trshoe	Момент привода правого ботинка
_Tlshoe	Момент привода левого ботинка
a	Расстояние от барабана центрируется к центру контакта стержня обуви
c	Расстояние от стержня обуви прикрепляет центр, чтобы тормозить связь привода на тормозной колодке
r	Барабан внутренний радиус
_Ba	Тормозите внутренний диаметр привода
Θ1	Угол от стержня обуви прикрепляет центр, чтобы запуститься материала тормозной колодки по обуви
Θ2	Угол от стержня обуви прикрепляет центр к концу материала тормозной колодки по обуви

Сопоставленный

Если вы задаете параметр Brake Type Mapped, блок использует интерполяционную таблицу, чтобы определить момент привода.

$T = {\begin{matrix} f_{b r a k e} (P, N) когда N \neq 0 \\ (\frac{μ_{s t a t i c}}{μ}) f_{b r a k e} (P, N) когда N = 0 \end{matrix}$

Уравнения используют эти переменные.

T	Момент привода
$f_{b r a k e}^{} (P, N)$	Интерполяционная таблица момента привода
P	Прикладное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент трения поверхности клавиатуры барабана взаимодействует через интерфейс при статических условиях
μ	Коэффициент трения интерфейса ротора клавиатуры диска

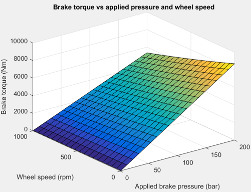
Интерполяционная таблица для момента привода, $f_{b r a k e}^{} (P, N)$ , функция прикладного тормозного давления и скорости колеса, где:

T является моментом привода в N · m.
P является примененным тормозным давлением в панели.
N является скоростью колеса в об/мин.

Порты

Входной параметр

развернуть все

`BrkPrs` — Тормозное давление
`scalar`

Тормозное давление, в Па.

Зависимости

Чтобы создать этот порт, для параметра Brake Type, задают один из этих типов:

Disc
Drum
Mapped

`AxlTrq` — Крутящий момент оси
`scalar`

Крутящий момент оси, _Ta, об оси вращения колеса, в N · m.

`Vx` — Продольная скорость
`scalar`

Ось продольная скорость, _Vx, вдоль зафиксированной шиной оси X, в m/s.

`Vy` — Боковая скорость
`scalar`

Скорость ответвления оси, _Vy, вдоль зафиксированной шиной оси Y, в m/s.

`Camber` — Угол изгиба
`scalar`

Угол изгиба, ɣ, в рад.

`YawRate` — Утомите скорость вращения
`scalar`

Утомите скорость вращения, r, о зафиксированной шиной оси z (уровень отклонения от курса), в rad/s.

`Prs` — Давление накачивания шин
`scalar`

Давление накачивания шин, _pi, в Па.

`Gnd` — Оснуйте смещение
`scalar`

Оснуйте смещение вдоль зафиксированного шиной z - ось в m. Положительный вход производит лифт колеса.

`Fext` — Сила оси прикладывается к шине
`scalar`

Сила оси применялась к шине, _Fext, вдоль зафиксированной транспортным средством оси z (положительный вход сжимает шину), в N · m.

`ScaleFctrs` — Масштабные коэффициенты
`array`

Волшебный массив масштабного коэффициента Формулы. Измерениями массива является 27 1.

Волшебные уравнения Формулы используют масштабные коэффициенты, чтобы составлять статический или изменения времени выполнения симуляции. Номинально, большинство установлено в 1.

Элемент массива	Переменная	ScaleFactor
`ScaleFctrs(1,1)`	`lam_Fzo`	Номинальная загрузка
`ScaleFctrs(2,1)`	`lam_mux`	Продольный пиковый коэффициент трения
`ScaleFctrs(3,1)`	`lam_muy`	Боковой пиковый коэффициент трения
`ScaleFctrs(4,1)`	`lam_muV`	Подсуньте скорость По сравнению с затухающим трением
`ScaleFctrs(5,1)`	`lam_Kxkappa`	Тормозите жесткость промаха
`ScaleFctrs(6,1)`	`lam_Kyalpha`	Движение на повороте жесткости
`ScaleFctrs(7,1)`	`lam_Cx`	Продольный масштабный фактор
`ScaleFctrs(8,1)`	`lam_Cy`	Боковой масштабный фактор
`ScaleFctrs(9,1)`	`lam_Ex`	Продольный фактор искривления
`ScaleFctrs(10,1)`	`lam_Ey`	Боковой фактор искривления
`ScaleFctrs(11,1)`	`lam_Hx`	Продольный горизонтальный сдвиг
`ScaleFctrs(12,1)`	`lam_Hy`	Боковой горизонтальный сдвиг
`ScaleFctrs(13,1)`	`lam_Vx`	Продольный вертикальный сдвиг
`ScaleFctrs(14,1)`	`lam_Vy`	Боковой вертикальный сдвиг
`ScaleFctrs(15,1)`	`lam_Kygamma`	Жесткость силы изгиба
`ScaleFctrs(16,1)`	`lam_Kzgamma`	Жесткость крутящего момента изгиба
`ScaleFctrs(17,1)`	`lam_t`	Пневматический след (производящий выравнивающий жесткость крутящего момента)
`ScaleFctrs(18,1)`	`lam_Mr`	Остаточный крутящий момент
`ScaleFctrs(19,1)`	`lam_xalpha`	Альфа-влияние на Fx (каппа)
`ScaleFctrs(20,1)`	`lam_ykappa`	Влияние каппы на Fy (альфа)
`ScaleFctrs(21,1)`	`lam_Vykappa`	Вызванный сгиб регулирует Fy
`ScaleFctrs(22,1)`	`lam_s`	Рука момента Fx
`ScaleFctrs(23,1)`	`lam_Cz`	Радиальная жесткость шины
`ScaleFctrs(24,1)`	`lam_Mx`	Опрокидывание жесткости пары
`ScaleFctrs(25,1)`	`lam_VMx`	Опрокидывание пары вертикальный сдвиг
`ScaleFctrs(26,1)`	`lam_My`	Момент сопротивления качению
`ScaleFctrs(27,1)`	`lam_Mphi`	Парковка крутящего момента Mz

Вывод

развернуть все

`Info` — Сигнал шины
шина

Сигнал шины, содержащий эти вычисления блока.

Сигнал	Описание	Модули
`AxlTrq`	Крутящий момент оси о зафиксированной колесом оси Y	N·
`Omega`	Скорость вращения колеса о зафиксированной колесом оси Y	rad/s
`Fx`	Продольная сила транспортного средства вдоль зафиксированной шиной оси X	N
`Fy`	Боковая сила транспортного средства вдоль зафиксированной шиной оси Y	N
`Fz`	Вертикальная сила транспортного средства вдоль зафиксированной шиной оси z	N
`Mx`	Опрокидывание момента о зафиксированной шиной оси X	N·
`My`	Крутящий момент сопротивления качению о зафиксированной шиной оси Y	N·
`Mz`	Выравнивание момента о зафиксированной шиной оси z	N·
`Vx`	Транспортное средство продольная скорость вдоль зафиксированной шиной оси X	m/s
`Vy`	Скорость ответвления транспортного средства вдоль зафиксированной шиной оси Y	m/s
`Re`	Загруженный эффективный радиус	m
`Kappa`	Продольное отношение промаха	Нет данных
`Alpha`	Угол заноса	рад
`a`	Свяжитесь с закрашенной фигурой половина длины	m
`b`	Свяжитесь с полушириной закрашенной фигуры	m
`Gamma`	Угол изгиба	рад
`psidot`	Утомите скорость вращения о зафиксированной шиной оси z (уровень отклонения от курса)	rad/s
`BrkTrq`	Момент привода о зафиксированной транспортным средством оси Y	N·
`BrkPrs`	Тормозное давление	Па
`z`	Ось вертикальное смещение вдоль зафиксированной шиной оси z	m
`zdot`	Ось вертикальная скорость вдоль зафиксированной шиной оси z	m/s
`Gnd`	Оснуйте смещение вдоль зафиксированной шиной оси z (положительный вход производит лифт колеса),	m
`GndFz`	Вертикальная сила боковой стены на земле вдоль зафиксированной шиной оси z	N
`Prs`	Давление накачивания шин	Па

`Omega` — Скорость вращения колеса
`scalar`

Скорость вращения колеса, ω, о зафиксированной колесом оси Y, в rad/s.

`Fx` — Продольная сила оси
`scalar`

Продольная сила, действующая на ось, _Fx, вдоль зафиксированной шиной оси X, в N. Положительная сила действует, чтобы переместить транспортное средство вперед.

`Fy` — Боковая сила оси
`scalar`

Боковая сила, действующая на ось, _Fy, вдоль зафиксированной шиной оси Y, в N.

`Fz` — Вертикальная сила оси
`scalar`

Вертикальная сила, действующая на ось, _Fz, вдоль зафиксированной шиной оси z, в N.

`Mx` — Опрокидывание момента
`scalar`

Продольный момент, действуя на ось, _Mx, о зафиксированной шиной оси X, в N · m.

`My` — Прокрутка резистивного момента
`scalar`

Боковой момент, действуя на ось, _My, о зафиксированной шиной оси Y, в N · m.

`Mz` — Выравнивание момента
`scalar`

Вертикальный момент, действуя на ось, _Mz, о зафиксированной шиной оси z, в N · m.

Параметры

развернуть все

Блокируйте опции

`Brake Type` — Выберите тип
`None` | `Disc` | `Drum` | `Mapped`

Используйте параметр Brake Type, чтобы выбрать тормоз.

Тормозите установку типа	Тормозите реализацию
`None`	'none'
`Disc`	Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие
`Drum`	Симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной момент
`Mapped`	Интерполяционная таблица, которая является функцией скорости колеса и примененного тормозного давления

Тормоз

`Static friction coefficient, mu_static` — Статическое трение
`scalar`

Статический коэффициент трения, безразмерный.

Зависимости

Чтобы включить этот параметр, для параметра Brake Type, задают один из этих типов:

Disc
Drum
Mapped

`Kinetic friction coefficient, mu_kinetic` — Кинетическое трение
`scalar`

Кинематический коэффициент трения, безразмерный.

Зависимости

Чтобы включить этот параметр, для параметра Brake Type, задают один из этих типов:

Disc
Drum
Mapped

Диск

`Disc brake actuator bore, disc_abore` — Расстояние скуки
`scalar`

Привод дискового тормоза перенес в m.

Зависимости

Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.

`Brake pad mean radius, Rm` — Радиус
`scalar`

Средний радиус тормозной колодки, в m.

Зависимости

Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.

`Number of brake pads, num_pads` количество
`scalar`

Количество тормозных колодок.

Зависимости

Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.