Документация

Что такое Вейвлет?

Вейвлет является формой волны эффективно ограниченного срока действия, который имеет среднее значение нулевой и ненулевой нормы.

Много сигналов и изображений интереса предоставляют кусочно-гладкое поведение, акцентированное переходными процессами. Речевые сигналы характеризуются кратковременными вспышками, кодирующими согласные, сопровождаемые установившимися колебаниями, показательными из гласных. Естественные изображения имеют ребра. Финансовые временные ряды предоставляют переходное поведение, которые характеризуют быстрые подъемы и спады в экономических условиях. В отличие от основания Фурье, основы вейвлета владеют мастерством разреженного представления кусочных регулярных сигналов и изображений, которые включают переходное поведение.

Сравните вейвлеты с синусоидами, которые являются основанием анализа Фурье. Синусоиды не имеют ограниченного срока действия — они расширяют от минус до плюс бесконечность. В то время как синусоиды являются гладкими и предсказуемы, вейвлеты имеют тенденцию быть неправильными и асимметричными.

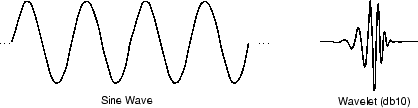
Анализ Фурье состоит из разбивания сигнала в синусоиды различных частот. Точно так же анализ вейвлета является разбиванием сигнала в переключенные и масштабированные версии оригинала (или родительский элемент) вейвлет.

Только смотря на изображения вейвлетов и синусоид, вы видите интуитивно, что сигналы с резкими изменениями могут лучше анализироваться с неправильным вейвлетом, чем со сглаженной синусоидой.

Это также целесообразно, что локальные функции могут быть описаны лучше с вейвлетами, которые имеют локальную степень. Следующий пример иллюстрирует это для простого сигнала, состоящего из синусоиды с разрывом.

t = linspace(0,1,100)';
x = sin(2*pi*t);
x1 = x-0.15;
y = zeros(size(x));
y(1:length(y)/2) = x(1:length(y)/2);
y(length(y)/2+1:end) = x1(length(y)/2+1:end);
stem(t,y,'markerfacecolor',[0 0 1]); 
xlabel('Seconds'); 
ylabel('Amplitude');

[swa,swd] = swt(y,1,'sym2');
subplot(211)
stem(t,y,'markerfacecolor',[0 0 1]); 
title('Original Signal');
subplot(212)
stem(t,swd,'markerfacecolor',[0 0 1]);
title('Level 1 Wavelet Coefficients');

dftsig = fft([x y]);
dftsig = dftsig(1:length(y)/2+1,:);
df = 100/length(y);
freq = 0:df:50;
stem(freq,abs(dftsig));
xlabel('Hz'); ylabel('Magnitude');
legend('sine wave','sine wave with discontinuity');

[swax,swdx] = swt(x,1,'sym2');
subplot(211)
stem(t,swd); title('Sine Wave with Discontinuity (Wavelet Coefficients)');
subplot(212)
stem(t,swdx); title('Sine Wave (Wavelet Coefficients)');