Вейвлет Daubechies фильтрует расчет
dbaux функция генерирует масштабирующиеся коэффициенты фильтра для "экстремальной фазы" вейвлеты Daubechies.
W = dbaux(N)N Daubechies, масштабирующий фильтр, таким образом, что sum(W) = 1.
Нестабильность может произойти когда N является слишком большим. Начиная со значений N в области значений 30-х функциональный выход больше не будет точно представлять масштабирующиеся коэффициенты фильтра.
Расчет dbN Daubechies, масштабирующий фильтр, требует экстракции корней полинома порядка 4N. Нестабильность может произойти, начавшись со значений N в 30-х.
Используемый алгоритм основан на результате, полученном Shensa [3], показывая соответствие между “лагранжевым à торусом” фильтры и сверточными квадратами фильтров вейвлета Daubechies.
Расчет порядка N Daubechies, масштабирующий фильтр w, продолжает на двух шагах: вычислите “лагранжев à торус”, фильтруют P и извлекают квадратный корень. Более точно:
P связанный “лагранжев à торус” фильтр является симметричным фильтром длины 4N-1. P задан
P = [a (N) 0 a (N-1) 0... 0 a (1) 1 a (1) 0 a (2) 0... 0 a (N)]
где
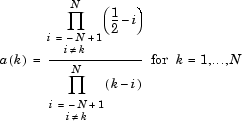
Затем если w обозначает dbN Daubechies, масштабирующий фильтр суммы![]() , w является квадратным корнем из P:
, w является квадратным корнем из P:
P = conv(wrev(w), w), где w является фильтром длины 2N.
Соответствующему полиному определили местоположение нулей N в −1 и нулях N−1 меньше чем 1 в модуле.
Обратите внимание на то, что другие методы могут использоваться; смотрите различные решения спектральной задачи разложения на множители в Странге-Нгуене [4] (p. 157).
[1] Daubechies, я. Десять Лекций по Вейвлетам, ряду конференции CBMS-NSF в прикладной математике, SIAM Эд., 1992.
[2] Оппенхейм, Алан V и Рональд В. Шафер. Обработка сигналов дискретного времени. Englewood Cliffs, NJ: Prentice Hall, 1989.
[3] Shensa, M.J. (1992), “Дискретный вейвлет преобразовывает: свадьба торус и Алгоритмы Mallat”, Сделка IEEE на Обработке сигналов, издании 40, 10, стр 2464-2482.
[4] Странг, G. и Т. Нгуен. Вейвлеты и наборы фильтров. Веллесли, MA: Wellesley-Кембриджское нажатие, 1996.