Прямая реконструкция от 1D коэффициентов вейвлета
Y = upcoef(O,X,wname,N)
Y = upcoef(O,X,wname,N,L)
Y = upcoef(O,X,Lo_R,Hi_R,N)
Y
= upcoef(O,X,Lo_R,Hi_R,N,L)
Y = upcoef(O,X,wname)
Y = upcoef(O,X,wname,1)
Y = upcoef(O,X,Lo_R,Hi_R)
Y = upcoef(O,X,Lo_R,Hi_R,1)
upcoef одномерная аналитическая функция вейвлета.
Y = upcoef(O,X, вычисляет wname,N)N- продвиньтесь восстановленные коэффициенты векторного X.
wname вектор символов или скаляр строки определение вейвлета. Смотрите wfilters для получения дополнительной информации.
N должно быть строго положительное целое число.
Если O = 'a', коэффициенты приближения восстановлены.
Если O = 'd', коэффициенты детали восстановлены.
Y = upcoef(O,X, вычисляет wname,N,L)N- продвиньтесь восстановленные коэффициенты векторного X и берет длину-L центральный фрагмент результата.
Вместо того, чтобы дать имя вейвлета, можно дать фильтры.
Для Y = upcoef(O,X,Lo_R,Hi_R,N) или Y
= upcoef(O,X,Lo_R,Hi_R,N,L), Lo_R реконструкция фильтр lowpass и Hi_R фильтр высоких частот реконструкции.
Y = upcoef(O,X, эквивалентно wname)Y = upcoef(O,X,.wname,1)
Y = upcoef(O,X,Lo_R,Hi_R) эквивалентно Y = upcoef(O,X,Lo_R,Hi_R,1).
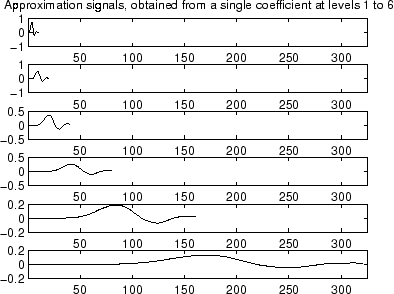
% The current extension mode is zero-padding (see dwtmode).
% Approximation signals, obtained from a single coefficient
% at levels 1 to 6.
cfs = [1]; % Decomposition reduced a single coefficient.
essup = 10; % Essential support of the scaling filter db6.
figure(1)
for i=1:6
% Reconstruct at the top level an approximation
% which is equal to zero except at level i where only
% one coefficient is equal to 1.
rec = upcoef('a',cfs,'db6',i);
% essup is the essential support of the
% reconstructed signal.
% rec(j) is very small when j is ≥ essup.
ax = subplot(6,1,i),h = plot(rec(1:essup));
set(ax,'xlim',[1 325]);
essup = essup*2;
end
subplot(611)
title(['Approximation signals, obtained from a single ' ...
'coefficient at levels 1 to 6'])
% Editing some graphical properties,
% the following figure is generated.
% The same can be done for details.
% Details signals, obtained from a single coefficient
% at levels 1 to 6.
cfs = [1];
mi = 12; ma = 30; % Essential support of
% the wavelet filter db6.
rec = upcoef('d',cfs,'db6',1);
figure(2)
subplot(611), plot(rec(3:12))
for i=2:6
% Reconstruct at top level a single detail
% coefficient at level i.
rec = upcoef('d',cfs,'db6',i);
subplot(6,1,i), plot(rec(mi*2^(i-2):ma*2^(i-2)))
end
subplot(611)
title(['Detail signals obtained from a single ' ...
'coefficient at levels 1 to 6'])
% Editing some graphical properties,
% the following figure is generated.

upcoef эквивалентно N время повторило, что использование обратного вейвлета преобразовывает.