Динамические сети могут быть разделены на две категории: те, которые имеют только связи feedforward и тех, которые имеют обратную связь, или текущий, связи. Чтобы изучить различия между статическими, динамическими feedforward, и текущими динамическими сетями, создайте некоторые сети и смотрите, как они отвечают на входную последовательность. (Сначала, вы можете хотеть рассмотреть Симуляцию с Последовательными Входными параметрами в Динамической Сети.)
Следующие команды создают импульсную входную последовательность и строят ее:
p = {0 0 1 1 1 1 0 0 0 0 0 0};
stem(cell2mat(p))

Теперь создайте статическую сеть и найдите сетевой ответ на импульсную последовательность. Следующие команды создают простую линейную сеть с одним слоем, одним нейроном, никаким смещением и весом 2:
net = linearlayer;
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = 2;
view(net)

Можно теперь симулировать сетевой ответ на импульсный вход и построить его:
a = net(p); stem(cell2mat(a))

Обратите внимание на то, что ответ статической сети длится пока входной импульс. Ответ статической сети в любое время точка зависит только от значения входной последовательности в том же самом моменте времени.
Теперь создайте динамическую сеть, но тот, который не имеет никаких связей обратной связи (единовременная сеть). Можно использовать ту же сеть, используемую в Симуляции с Параллельными Входными параметрами в Динамической Сети, которая была линейной сетью с коснувшейся линией задержки на входе:
net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = [1 1];
view(net)

Можно снова симулировать сетевой ответ на импульсный вход и построить его:
a = net(p); stem(cell2mat(a))

Ответ динамической сети длится дольше, чем входной импульс. Динамическая сеть имеет память. Его ответ в любой момент времени зависит не только от текущего входа, но и от истории входной последовательности. Если сеть не будет иметь никаких связей обратной связи, то только конечная сумма истории будет влиять на ответ. В этом рисунке вы видите, что ответ на импульс длится один временной шаг вне импульсной длительности. Это вызвано тем, что коснувшаяся линия задержки на входе имеет максимальную задержку 1.
Теперь рассмотрите простую текущую динамическую сеть, показанную в следующем рисунке.
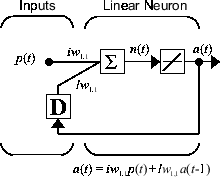
Можно создать сеть, просмотреть ее и симулировать ее со следующими командами. narxnet команда обсуждена в Ряду Времени проектирования Нейронные сети Обратной связи NARX.
net = narxnet(0,1,[],'closed');
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.LW{1} = .5;
net.IW{1} = 1;
view(net)

Следующие команды строят сетевой ответ.
a = net(p); stem(cell2mat(a))

Заметьте, что текущие динамические сети обычно имеют более длительный ответ, чем динамические feedforward сети. Для линейных сетей динамические feedforward сети называются конечной импульсной характеристикой (FIR), потому что ответ на импульсный вход станет нулевым после конечного количества времени. Линейные текущие динамические сети называются бесконечной импульсной характеристикой (IIR), потому что ответ на импульс может затухнуть, чтобы обнулить (для устойчивой сети), но это никогда не будет становиться точно равным нулю. Импульсная характеристика для нелинейной сети не может быть задана, но идеи конечных и бесконечных ответов действительно переносят.
Динамические сети обычно более мощны, чем статические сети (несмотря на то, что несколько более трудный, чтобы обучаться). Поскольку динамические сети имеют память, они могут быть обучены изучить последовательные или изменяющиеся во времени шаблоны. Это имеет приложения в таких разрозненных областях как предсказание на финансовых рынках [RoJa96], эквализация канала в системах связи [FeTs03], обнаружение фазы в энергосистемах [KaGr96], сортируя [JaRa04], обнаружение отказа [ChDa99], распознавание речи [Robin94], и даже предсказание структуры белка в генетике [GiPr02]. Можно найти обсуждение намного более динамических сетевых приложений в [MeJa00].
Одно основное приложение динамических нейронных сетей находится в системах управления. Это приложение обсуждено подробно в Системах управления Нейронной сети. Динамические сети также хорошо подходят для фильтрации. Вы будете видеть использование некоторых линейных динамических сетей для просачивания, и некоторые из тех идей расширены в этой теме, с помощью нелинейных динамических сетей.
Программное обеспечение Deep Learning Toolbox™ спроектировано, чтобы обучаться, класс сети вызвал Многоуровневую цифровую динамическую сеть (LDDN). Любая сеть, которая может быть расположена в форме LDDN, может быть обучена с тулбоксом. Вот основное описание LDDN.
Каждый слой в LDDN составлен из следующих частей:
Набор матриц веса, которые входят в тот слой (который может соединиться от других слоев или от внешних входных параметров), сопоставленное правило функции веса раньше комбинировал матрицу веса с ее входом (обычно стандартное умножение матриц, dotprod), и сопоставленная коснувшаяся линия задержки
Вектор смещения
Сетевое правило функции ввода, которое использовано, чтобы объединить выходные параметры различных функций веса со смещением, чтобы произвести сетевой вход (обычно соединение подведения итогов, netprod)
Передаточная функция
Сеть имеет входные параметры, которые соединены со специальными весами, названными входными весами, и обозначены IWi,j (net.IW{i,j} в коде), где j обозначает количество входного вектора, который вводит вес, и i обозначает количество слоя, с которым соединяется вес. Веса, соединяющие один слой с другим, называются весами слоя и обозначаются LWi,j (net.LW{i,j} в коде), где j обозначает, количество слоя, входя в вес и i обозначает количество слоя при выходе веса.
Следующая фигура является примером LDDN с тремя слоями. Первый слой имеет три веса, сопоставленные с ним: один входной вес, вес слоя от слоя 1 и вес слоя от слоя 3. Два веса слоя коснулись линий задержки, сопоставленных с ними.

Программное обеспечение Deep Learning Toolbox может использоваться, чтобы обучить любой LDDN, пока вес функционирует, сетевые функции ввода, и передаточные функции имеют производные. Большинство известных динамических сетевых архитектур может быть представлено в форме LDDN. В остатке от этой темы вы будете видеть, как использовать некоторые простые команды, чтобы создать и обучить несколько очень мощных динамических сетей. Другие сети LDDN, не покрытые этой темой, могут быть созданы с помощью типовой сетевой команды, как объяснено в Задают Мелкие Архитектуры Нейронной сети.
Динамические сети обучены в программном обеспечении Deep Learning Toolbox с помощью тех же основанных на градиенте алгоритмов, которые были описаны в Многоуровневых Мелких Нейронных сетях и Обучении Обратной связи. Можно выбрать из любой из учебных функций, которые были представлены в той теме. Примеры обеспечиваются в следующих разделах.
Несмотря на то, что динамические сети могут быть обучены с помощью тех же основанных на градиенте алгоритмов, которые используются в статических сетях, производительность алгоритмов в динамических сетях может очень отличаться, и градиент должен быть вычислен более комплексным способом. Считайте снова простую текущую сеть показанной в этом рисунке.

Веса оказывают два различных влияния на сетевой выход. Первым является прямое влияние, потому что изменение в весе вызывает мгновенное изменение в выходе на шаге текущего времени. (Этот первый эффект может быть вычислен с помощью стандартной обратной связи.) Вторым является косвенное воздействие, потому что некоторые входные параметры к слою, такие как a (t − 1), являются также функциями весов. Чтобы составлять это косвенное воздействие, необходимо использовать динамическую обратную связь, чтобы вычислить градиенты, который более в вычислительном отношении интенсивен. (См. [DeHa01a], [DeHa01b] и [DeHa07].) Ожидают, что динамическая обратная связь займет больше времени, чтобы обучаться, частично поэтому. Кроме того, ошибочные поверхности для динамических сетей могут быть более комплексными, чем те для статических сетей. Обучение, более вероятно, будет захвачено в локальных минимумах. Это предполагает, что вы можете должны быть обучить сеть несколько раз, чтобы достигнуть оптимального результата. См. [DHH01] и [HDH09] для некоторого обсуждения обучения динамических сетей.
Остающиеся разделы этой темы показывают, как создать, обучить, и применить определенные динамические сети к моделированию, обнаружению и прогнозированию проблем. Некоторые сети требуют динамической обратной связи для вычисления градиентов, и другие не делают. Как пользователь, вы не должны решать, необходима ли динамическая обратная связь. Это определяется автоматически программным обеспечением, которое также выбирает лучшую форму динамической обратной связи, чтобы использовать. Только необходимо создать сеть и затем вызвать стандартный train команда.