Многомерные форматы данных временных рядов

Первый шаг в многомерном анализе временных рядов должен получить, смотреть и предварительно обработать данные. Эта тема описывает следующее:

Как загрузить экономические данные в MATLAB^®
Соответствующие типы данных и структуры для многомерных аналитических функций временных рядов
Общие характеристики данных временных рядов, которые могут гарантировать преобразование набора перед продолжением анализа
Как разделить ваши данные в предварительную выборку, оценку, и предсказать выборки.

Многомерные данные временных рядов

Два основных типа многомерных данных временных рядов:

Данные об ответе – Наблюдения от n-D многомерный временной ряд ответов y _t (см. Типы Стационарных Многомерных Моделей Временных рядов).
Внешние данные – Наблюдения от m-D многомерные временные ряды предикторов _xt. Каждая переменная во внешних данных появляется во всех уравнениях ответа по умолчанию.

Прежде, чем задать любой набор данных, когда вход к Econometrics Toolbox™ функционирует, отформатируйте данные соответственно. Используйте стандартные команды MATLAB или предварительно обработайте данные с программой электронной таблицы, программой базы данных, Perl или другим инструментом.

Можно получить исторические данные временных рядов из нескольких источников в свободном доступе, таких как Экономическая База данных Федеральной резервной системы Сент-Луиса (известный как FRED^®): https://research.stlouisfed.org/fred2/. Если у вас есть лицензия Datafeed Toolbox™, можно использовать функции тулбокса, чтобы получить доступ к данным из различных источников.

Загрузите многомерные экономические данные

Файл Data_USEconModel поставки с Econometrics Toolbox. Это содержит временные ряды от FRED.

Загрузите данные в рабочее пространство MATLAB.

load Data_USEconModel

Переменные в рабочей области включают:

Data, 249 14 матрица, содержащая 14 макроэкономических временных рядов.
DataTable, 249 14 массив расписания MATLAB, содержащий данные, к которым добавляют метку времени.
dates, вектор с 249 элементами, содержащий MATLAB последовательные даты выборки представления чисел даты. Последовательный номер даты является номером дней с 1 января, 0000. (Эта "дата" не является действительной датой, но удобна для того, чтобы сделать вычисления даты. Для получения дополнительной информации смотрите Форматы даты (Financial Toolbox) в Руководстве пользователя Financial Toolbox™.)
Description, символьный массив, содержащий описание ряда данных и ключа к меткам для каждого ряда.
series, 1 14 массив ячеек меток для временных рядов.

DataTable содержит те же данные как Data. Однако как таблица, расписание позволяет вам использовать запись через точку, чтобы получить доступ к переменной. Например, DataTable.UNRATE задает временные ряды уровня безработицы. Все расписания содержат переменную Time, который является datetime вектор меток времени наблюдения. Для получения дополнительной информации см. Создание объекта Timetable (MATLAB) и Представления дат и времени в MATLAB (MATLAB). Можно также работать с MATLAB последовательные числа даты, сохраненные в dates.

Отобразите первое и последнее время выборки и имена переменных при помощи DataTable.

firstperiod = DataTable.Time(1)

firstperiod = datetime
   Q1-47

lastperiod = DataTable.Time(end)

lastperiod = datetime
   Q1-09

seriesnames = DataTable.Properties.VariableNames

seriesnames = 1x14 cell
  Columns 1 through 6

    {'COE'}    {'CPIAUCSL'}    {'FEDFUNDS'}    {'GCE'}    {'GDP'}    {'GDPDEF'}

  Columns 7 through 12

    {'GPDI'}    {'GS10'}    {'HOANBS'}    {'M1SL'}    {'M2SL'}    {'PCEC'}

  Columns 13 through 14

    {'TB3MS'}    {'UNRATE'}

Эта таблица описывает переменные в DataTable.

ФРЕД Вэриэбл	Описание
`COE`	Заплаченная компенсация сотрудников в $ миллиарды
`CPIAUCSL`	Индекс потребительских цен (CPI)
`FEDFUNDS`	Эффективная ставка по федеральным фондам
`GCE`	Правительственные расходы потребления и инвестиции в $ миллиарды
`GDP`	Валовой внутренний продукт (ВВП)
`GDPDEF`	Валовой внутренний продукт в $ миллиарды
`GPDI`	Грубые частные внутренние инвестиции в $ миллиарды
`GS10`	Десятилетняя доходность казначейских облигаций
`HOANBS`	Несельскохозяйственный индекс делового сектора часов работал
`M1SL`	Денежная масса M1 (узкие деньги)
`M2SL`	Денежная масса M2 (широкие деньги)
`PCEC`	Частные потребительские расходы в $ миллиарды
`TB3MS`	Трехмесячный доход по казначейским векселям
`UNRATE`	Уровень безработицы

Рассмотрите изучение динамики GDP, CPI и уровня безработицы, и предположите, что правительственные расходы потребления являются внешней переменной. Создайте массивы для данных о предикторе и ответа. Отобразите последнее наблюдение в каждом массиве.

Y = DataTable{:,["CPIAUCSL" "UNRATE" "GDP"]};
x = DataTable.GCE;

lastobsresponse = Y(end,:)

lastobsresponse = 1×3
10⁴ ×

    0.0213    0.0008    1.4090

lastobspredictor = x(end)

lastobspredictor = 2.8833e+03

Y и x представляйте один путь наблюдений, и соответственно отформатированы для передачи многомерным функциям объекта модели. Информация о метке времени не применяется к массивам, потому что исследования принимают, что время выборки равномерно расположено с интервалами.

Многомерный формат данных

Обычно, вы загружаете ответ и наборы данных предиктора в рабочее пространство MATLAB как числовые массивы, таблицы MATLAB или расписания MATLAB. Однако многомерные функции объекта временных рядов принимают 2D или 3-D числовые массивы только, и необходимо задать ответ и данные о предикторе как отдельные входные параметры.

Тип переменной и проблемного контекста определяет формат данных, которыми вы снабжаете. Для любого массива, содержащего многомерные данные временных рядов:

Строка t массива содержит наблюдения за всеми переменными во время t.
Столбец j массива содержит все наблюдения за переменной j. MATLAB обрабатывает каждую переменную в массиве как отличную.

Матрица A данных указывает на один демонстрационный путь. Чтобы создать переменную, представляющую один путь длины T данных об ответе, поместите данные в T-by-n матричный Y:

$[\begin{matrix} y_{1, 1} & y_{2, 1} & \dots & y_{n, 1} \\ y_{1, 2} & y_{2, 2} & \dots & y_{n, 2} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ y_{1, T} & y_{2, T} & \dots & y_{n, T} \end{matrix}] .$

Yt J) = _j,t y, который является наблюдением t переменной отклика j. Один путь данных, созданных из переменных предикторов или других переменных, имеет подобную форму.

Можно задать один путь наблюдений как вход ко всем многомерным функциям объекта модели, которые принимают данные. Примеры ситуаций, в которых вы предоставляете один путь, включают:

Подходящий ответ и данные о предикторе к модели VARX. Вы предоставляете и путь данных об ответе и путь данных о предикторе, видите estimate.
Инициализируйте модель VEC путем преддемонстрационных данных для прогнозирования или симуляции путей (см. forecast или simulate).
Получите один путь к ответу из пропущения пути инноваций через модель VAR (см. filter).
Сгенерируйте условные прогнозы из модели VAR, учитывая путь будущих данных об ответе (см. forecast).

3-D числовой массив указывает на несколько независимых демонстрационных путей данных. Можно создать T-by-n-by-p массив Y, представление демонстрационных путей p данных об ответе, путем укладки одного путей ответов (матрицы) по третьему измерению.

Yt JK) = _j y_{, t, k}, который является наблюдением t переменной отклика j от пути k, k = 1, …, p. Все пути должны иметь те же шаги расчета, и переменные среди путей должны соответствовать. Для получения дополнительной информации смотрите Многомерные массивы (MATLAB).

Можно задать массив разнообразных путей ответов или инноваций как вход к нескольким многомерным функциям объекта модели, которые принимают данные. Примеры ситуаций, в которых вы предоставляете разнообразные пути, включают:

Инициализируйте модель VEC разнообразными путями преддемонстрационных данных для прогнозирования или симуляции разнообразных путей. Каждый заданный путь может представлять различные начальные условия, от которых функции генерируют прогнозы или симуляции.
Получите пути ко множественному ответу из пропущения разнообразных путей инноваций через модель VAR. Этот процесс является альтернативным способом симулировать пути ко множественному ответу.
Сгенерируйте несколько условных путей к прогнозу из модели VAR, данной разнообразные пути будущих данных об ответе.

estimate не поддерживает спецификацию разнообразных путей данных об ответе.

Внешний формат данных

Все многомерные функции объекта модели, которые берут внешние данные в качестве входа, принимают матричный X, представляющий один путь наблюдений. MATLAB включает все внешние переменные в компонент регрессии каждого уравнения ответа. Для модели VAR (p) уравнения ответа:

$[\begin{matrix} y_{1, t} \\ y_{2, t} \\ ⋮ \\ y_{n, t} \end{matrix}] = c + δ t + [\begin{matrix} x_{1, t} β (1, 1) + \dots + x_{m, t} β (1, m) \\ x_{1, t} β (2, 1) + \dots + x_{m, t} β (2, m) \\ ⋮ \\ x_{1, t} β (n, 1) + \dots + x_{m, t} β (n, m) \end{matrix}] + \sum_{j = 1}^{p} Φ_{j} y_{t - j} + ε_{t} .$

Чтобы сконфигурировать компоненты регрессии уравнений ответа, работайте с матрицей коэффициента регрессии (сохраненный в Beta свойство объекта модели), а не данные. Для получения дополнительной информации смотрите, Создают Модель VAR и Выбирают Exogenous Variables for Response Equations.

Многомерные функции объекта модели не поддерживают разнообразные пути данных о предикторе. Однако, если вы задаете путь информационных каналов предиктора и разнообразные пути ответа или инновационных данных, функция сопоставляет те же данные о предикторе ко всем путям. Например, если вы симулируете пути ответов из модели VARX и задаете разнообразные пути преддемонстрационных значений, simulate применяет те же внешние данные к каждому сгенерированному пути к ответу.

Предварительная Обработка Данных

Ваши данные могут иметь характеристики, которые нарушают предположения модели. Например, у вас могут быть данные с экспоненциальным ростом или данные из многочисленных источников в различных периодичностях. В таких случаях предварительно обработайте или преобразуйте данные к приемлемой форме для анализа.

Смотрите данные для отсутствующих значений, которые обозначаются NaNs. По умолчанию объектные функции используют мудрое списком удаление, чтобы удалить наблюдения, содержащие по крайней мере одно отсутствующее значение. Если по крайней мере одна переменная отклика или переменный предиктор имеют отсутствующее значение, какое-то время указывают (строка), MATLAB удаляет все наблюдения в течение того времени (целая строка ответа и матриц данных о предикторе). Такое удаление может иметь последствия на основе времени и эффективном объеме выборки. Поэтому необходимо исследовать и обратиться к любым отсутствующим значениям прежде, чем запустить анализ.
Для данных из многочисленных источников необходимо решить, как синхронизировать данные. Синхронизация данных может включать агрегацию данных или дезагрегацию, и последний может создать шаблоны отсутствующих значений. Можно обратиться к этим типам вызванных отсутствующих значений путем приписывания предыдущих значений (то есть, отсутствующее значение неизменно от своего предыдущего значения), или путем интерполяции их от соседних значений.
Если временные ряды являются переменными в расписании, то можно синхронизировать данные при помощи synchronize.
Для временных рядов, показывающих экспоненциальный рост, можно предварительно обработать данные путем взятия логарифма растущего ряда. В некоторых случаях необходимо применить первое различие результата (см. price2ret). Для получения дополнительной информации о стабилизации временных рядов смотрите Модульную Корневую Нестационарность. Для примера смотрите Тематическое исследование Модели VAR.

Примечание

Если вы применяете первое различие ряда, получившийся ряд является одним наблюдением короче, чем исходный ряд. Если вы применяете первое различие только некоторых временных рядов в наборе данных, обрезаете другой ряд так, чтобы все имели ту же длину или заполнили differenced ряд начальными значениями.

Базовые разделы времени для оценки

То, когда вы подбираете модель временных рядов к данным, отстало, члены в модели требуют инициализации, обычно с наблюдениями в начале выборки. Кроме того, чтобы измерить качество прогнозов из модели, необходимо протянуть данные в конце выборки от оценки. Поэтому прежде, чем анализировать данные, разделите основу времени максимум в трех последовательных, непересекающихся интервалов:

Преддемонстрационный период – Содержит данные, используемые, чтобы инициализировать изолированные значения в модели. И VAR (p) и VEC (p –1) модели требуют преддемонстрационного периода, содержащего, по крайней мере, p многомерные наблюдения. Например, если вы подбираете модель VAR (4), условное ожидаемое значение y_{, t}, учитывая его историю, содержит y _{t – 1}, y _{t – 2}, y _{t – 3}, и y _{t – 4}. Условное ожидаемое значение y ₅ является функцией y ₁, y ₂, y ₃, и y ₄. Поэтому вклад вероятности y ₅ требует _1–y4 y, который подразумевает, что данные не существуют для вкладов вероятности _1–y4 y. В этом случае оценка модели требует преддемонстрационного периода по крайней мере четырех моментов времени.
Период оценки – Содержит наблюдения y _t и x _t, к которому модель является явным образом подходящей. Количество наблюдений в выборке оценки является эффективным объемом выборки. В идентификационных целях модели эффективный объем выборки должен быть, по крайней мере, количеством параметров модели.
Предскажите период – Период, в который прогнозы сгенерированы, или forecast horizon. Этот раздел, который является дополнительным, содержит данные о затяжке для валидации предсказуемости модели.

Предположим y_{, t} является 2D рядом ответа и x_{, t} является 1D внешним рядом. Считайте подбирать модель VARX(p) для y _t к данным об ответе в T-by-2 матричный Y и внешние данные в T-by-1 векторный x. Кроме того, вы хотите, чтобы горизонт прогноза имел длину K (то есть, вы хотите протянуть наблюдения K в конце выборки, чтобы выдержать сравнение с прогнозами от подобранной модели). Этот рисунок показывает базовые разделы времени для оценки модели.

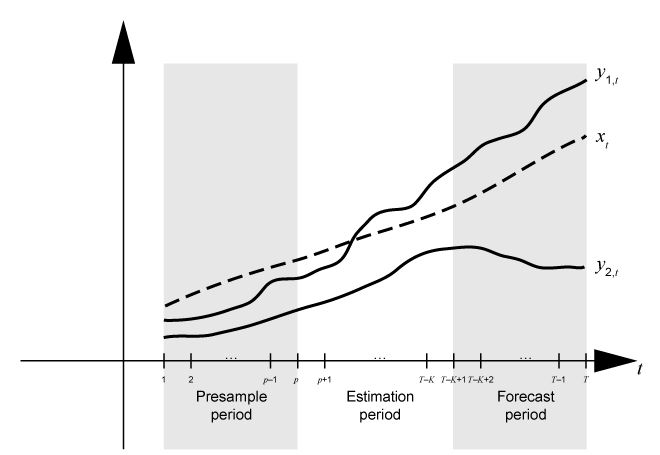
Этот рисунок показывает, какие фрагменты массивов соответствуют аргументам estimate.

В фигуре:

Y необходимый вход для определения данных об ответе, к которым модель является подходящей.
Y0 дополнительный аргумент пары "имя-значение" для определения преддемонстрационных данных об ответе. Y0 должен иметь, по крайней мере, строки p; estimate использование только последние наблюдения p Y0 ((конец – p + 1): конец инициализировать модель.
X дополнительный аргумент пары "имя-значение" для определения внешних данных для компонента регрессии модели.

Если вы не задаете Y0, estimate удаляет наблюдения 1 через p от Y инициализировать модель, и затем подбирает модель к остальной части данных Y ((p + 1): конец. Таким образом, estimate выводит периоды предварительной выборки и оценки из Y. Несмотря на то, что estimate извлекает предварительную выборку из Y по умолчанию можно извлечь предварительную выборку из данных и задать его с помощью Y0 аргумент пары "имя-значение", который гарантирует тот estimate инициализирует и подбирает модель к вашим техническим требованиям.

По умолчанию, estimate исключает компонент регрессии из модели, независимо от ли коэффициент регрессии Beta непустое свойство объекта модели. Если вы задаете X, estimate принимает эти меры:

Если вы задаете X, estimate синхронизирует X и Y относительно последнего наблюдения в массивах (T –K в предыдущей фигуре), и применяет только необходимое количество наблюдений к компоненту регрессии. Это действие подразумевает тот X может иметь больше строк что Y.
Если вы задаете X не задавайте Y0, estimate рассматривает первые строки p X как преддемонстрационные внешние данные и игнорирует их.

Если вы планируете подтвердить предсказательную силу подобранной модели, необходимо извлечь выборку прогноза из набора данных перед оценкой.

Раздел многомерные данные временных рядов для оценки

Считайте подбирать модель VAR (4) к данным и переменным в Загрузке Многомерными Экономическими данными и предложением прошлые 2 года данных, чтобы подтвердить предсказательную силу подобранной модели.

Идентифицируйте все строки в ответе и данных о предикторе, которые содержат по крайней мере одно отсутствующее значение.

catdata = [Y x];
whichmissing = any(isnan(catdata),2);
idxmissing = find(whichmissing)

idxmissing = 4×1

     1
     2
     3
     4

catdata(idxmissing,:)

ans = 4×4

   22.0000       NaN  237.2000   36.3000
   22.0800       NaN  240.5000   36.6000
   22.8400       NaN  244.6000   36.4000
   23.4100       NaN  254.4000   36.3000

Уровень безработицы имеет четыре ведущих отсутствующих значения.

Удалите все наблюдения, которые содержат ведущие отсутствующие значения из данных о предикторе и ответа.

Y = Y(~whichmissing,:);
x = x(~whichmissing);

Модель VAR (4) требует 4 преддемонстрационных ответов, и выборка прогноза требует 2 лет или 8 четвертей, данных. Разделите данные об ответе в предварительную выборку, оценку, и предскажите демонстрационные переменные. Разделите данные о предикторе в оценку и предскажите демонстрационные переменные (преддемонстрационные данные о предикторе не рассматриваются оценкой).

p = 4;
fh = 8;       
T = size(Y,1);

idxpre = 1:p;
idxest = (p + 1):(T - fh);
idxfor = (T - fh + 1):T;

Y0 = Y(idxpre,:);   % Presample
YF = Y(idxfor,:);   % Forecast sample
Y = Y(idxest,:);    % Estimation sample

xf = x(idxfor);
x = x(idxest);

При оценке модели с помощью estimate, задайте varm шаблон модели, представляющий модель VAR (4) и демонстрационные данные об ответе оценки Y как входные параметры. Задайте преддемонстрационные данные об ответе Y0 инициализировать модель при помощи 'Y0' аргумент пары "имя-значение", и задает демонстрационные данные о предикторе оценки x при помощи 'X' аргумент пары "имя-значение". Y и x синхронизируемые наборы данных, в то время как Y0 происходит в предыдущие четыре периода, прежде чем выборка оценки запустится.

После оценки можно предсказать модель с помощью forecast путем определения предполагаемого VARX (4) объект модели, возвращенный estimate, горизонт прогноза fh, и демонстрационные данные об ответе оценки Y инициализировать модель для прогнозирования. Задайте демонстрационные данные о предикторе прогноза xf для компонента регрессии модели при помощи 'X' аргумент пары "имя-значение". Определите предсказательную силу модели оценки путем сравнения прогнозов с демонстрационными данными об ответе прогноза YF.

Документация