Постройте данные временных рядов Используя приложение Econometric Modeler

Эти примеры показывают, как построить одномерные и многомерные данные временных рядов при помощи приложения Econometric Modeler. После графического вывода временных рядов можно взаимодействовать с графиками.

Постройте одномерные данные временных рядов

В этом примере показано, как построить одномерные данные временных рядов, затем наложите полосы рецессии в графике. Набор данных содержит ежеквартальные цены валового внутреннего продукта (ВВП) США от 1 947 до 2005.

В командной строке загрузите Data_GDP.mat набор данных.

load Data_GDP

Data содержит временной ряд и dates содержит время выборки как последовательные числа даты.

Преобразуйте время выборки в datetime вектор. Удалите часы, минуты и секунды от вектора datetime.

dates = datetime(dates,'ConvertFrom','datenum','Format',"yyyy-MM-dd");

Создайте расписание, содержащее данные, и сопоставьте каждую строку с соответствующим временем выборки в dates.

DataTable = timetable(Data,'RowTimes',dates,'VariableNames',"GDP");

В командной строке откройте приложение Econometric Modeler.

econometricModeler

В качестве альтернативы откройте приложение из галереи Apps (см. Econometric Modeler).

Импортируйте DataTable в приложение:

На вкладке Econometric Modeler, в разделе Import, нажатии кнопки.
В диалоговом окне Import Data, в столбце Import?, устанавливают флажок для DataTable переменная.
Нажмите Import.

Переменная GDP появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(GDP).

Наложите полосы рецессии путем щелчка правой кнопкой по графику и окну рисунка, затем выбора Show Recessions.

Наложите сетку путем приостановки на графике и нажатии.

Фокусируйтесь на GDP от 1 970 в конец периода выборки:

Сделайте паузу на графике, затем щелкните.
Расположите перекрестие в (1970,12000), затем перетащите перекрестие к (2005,3500).

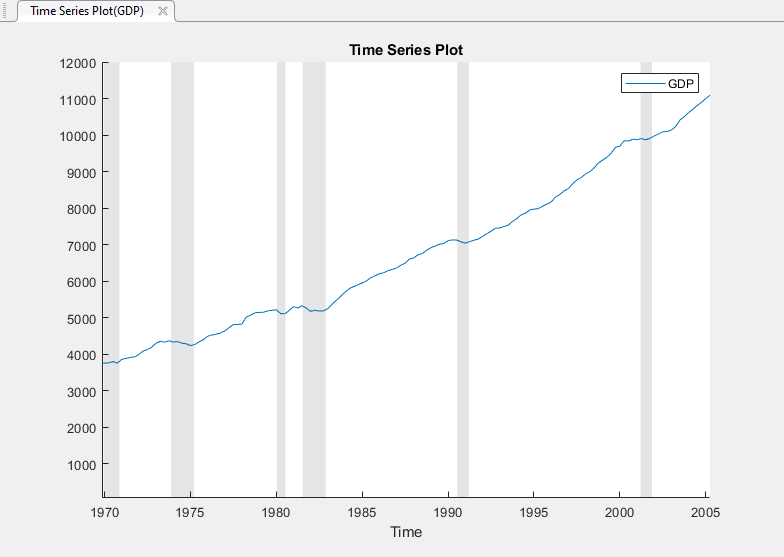
GDP кажется плоским или уменьшающимся прежде и в периоды рецессии.

Постройте многомерные временные ряды и корреляции

В этом примере показано, как построить несколько рядов на том же графике временных рядов, взаимодействуйте с получившимся графиком и постройте корреляции среди переменных. Набор данных, сохраненный в Data_Canada, содержит ежегодную канадскую инфляцию и процентные ставки от 1 954 до 1994.

В командной строке загрузите Data_Canada.mat набор данных.

load Data_Canada

Преобразуйте таблицу DataTable к расписанию:

Очистите имена строки DataTable.
Преобразуйте годы выборки в datetime вектор.
Преобразуйте таблицу в расписание путем соединения строк со временем выборки в dates.

DataTable.Properties.RowNames = {};
dates = datetime(dates,12,31,'Format','yyyy');
DataTable = table2timetable(DataTable,'RowTimes',dates);

В командной строке откройте приложение Econometric Modeler.

econometricModeler

В качестве альтернативы откройте приложение из галереи Apps (см. Econometric Modeler).

Импортируйте DataTable в приложение:

На вкладке Econometric Modeler, в разделе Import, нажатии кнопки.
В диалоговом окне Import Data, в столбце Import?, устанавливают флажок для DataTable переменная.
Нажмите Import.

Канадская процентная ставка и переменные уровня инфляции появляются в Data Browser, и график временных рядов, содержащий весь ряд, появляется в окне рисунка Time Series Plot(INF_C).

Наложите полосы рецессии путем щелчка правой кнопкой по графику и выбора Show Recessions.

Наложите сетку путем приостановки на графике и нажатии.

Удалите уровень инфляции (INF_C и INF_G) из графика временных рядов:

Щелкните правой кнопкой по графику.
Укажите на Show Time Series, затем ясный INF_C.
Повторите шаги 1 и 2, но очистите INF_G вместо этого.

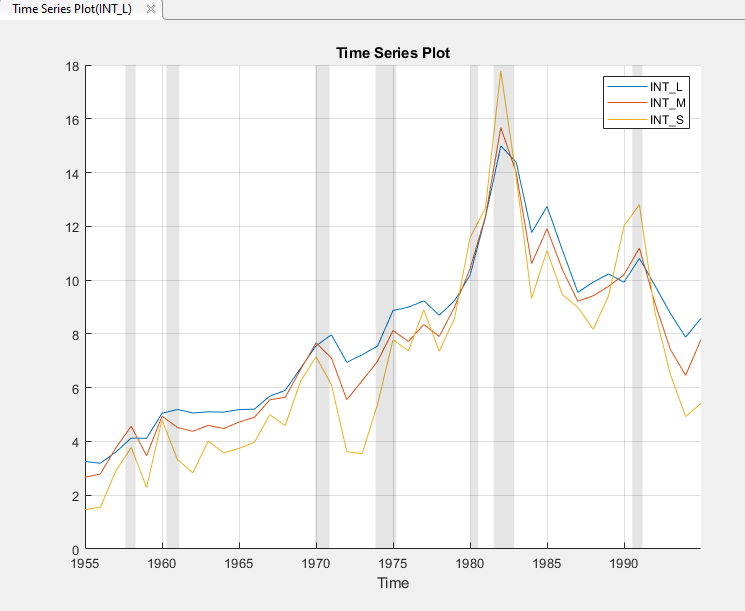
Сгенерируйте график корреляции для всех переменных:

Выберите все переменные в Data Browser.
Кликните по вкладке Plots, затем нажмите Correlations.

График корреляций появляется в окне рисунка Correlations(INF_C).

Удалите уровень инфляции на основе GDP (INF_G) из графика корреляций:

Щелкните правой кнопкой по графику.
Укажите на Show Time Series, затем ясный INF_G.

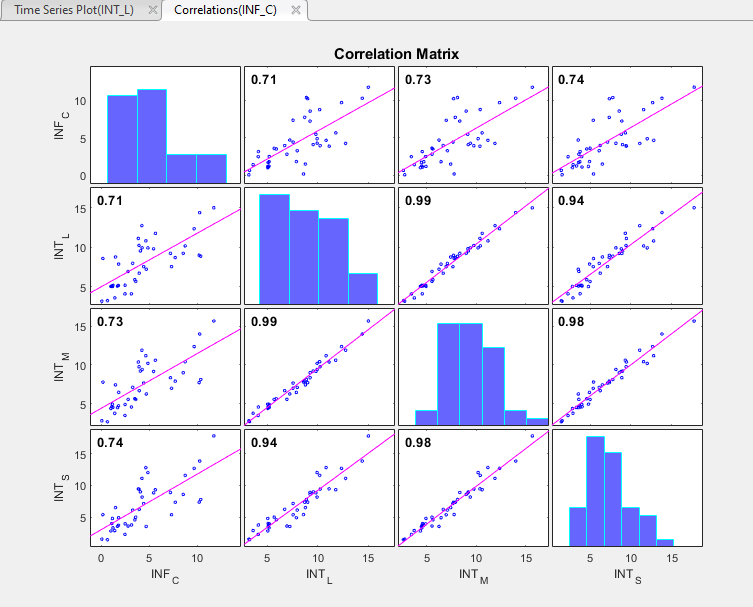
Все переменные, кажется, скашиваются направо. Согласно Коэффициентам корреляции пирсона (верхний левый из недиагональных графиков):

Уровень инфляции объясняет по крайней мере 70% изменчивости в процентных ставках (когда используется в качестве предиктора в линейной регрессии).
Процентные ставки высоко коррелируются; каждый объясняет по крайней мере 94% изменчивости в другом ряду.

Документация