В этом разделе описываются характеристики решателя Global Optimization Toolbox. Раздел включает рекомендации для получения результатов эффективнее.
Чтобы достигнуть лучше или более быстрые решения, сначала попытайтесь настроить рекомендуемые решатели путем установки подходящих вариантов или границ. Если результаты являются неудовлетворительными, попробуйте другие решатели.
| Требуемое решение | Сглаживайте цель и ограничения | Не сглаживайте цель или ограничения |
|---|---|---|
| Объяснение “требуемого решения” | Выбор между решателями для сглаженных проблем | Выбор между решателями для несглаженных проблем |
| Одно локальное решение | Функции Optimization Toolbox™; см. Таблицу решений Оптимизации (Optimization Toolbox) | fminbnd, patternsearchfminsearch, ga, particleswarm, simulannealbnd, surrogateopt |
| Несколько локальных решений | GlobalSearch, MultiStart | patternsearch, ga, particleswarm, simulannealbnd, или surrogateopt запущенный с нескольких начальной буквы указывает x0 или от нескольких начальных генеральных совокупностей |
| Одно глобальное решение | GlobalSearch, MultiStart, patternsearch, particleswarm, ga, simulannealbnd, surrogateopt | patternsearch, ga, particleswarm, simulannealbnd, surrogateopt |
| Одно локальное решение с помощью параллельной обработки | MultiStart, Функции Optimization Toolbox | patternsearch, ga, particleswarm, surrogateopt |
| Несколько локальных решений с помощью параллельной обработки | MultiStart | patternsearch, ga, или particleswarm запущенный с нескольких начальной буквы указывает x0 или от нескольких начальных генеральных совокупностей |
| Одно глобальное решение с помощью параллельной обработки | MultiStart | patternsearch, ga, particleswarm, surrogateopt |
Чтобы изучить значение условий в “Требуемом решении”, рассмотрите пример
f (x) =100x2 (1–x) 2–x,
который имеет локальные минимумы x1 около 0 и x2 около 1:
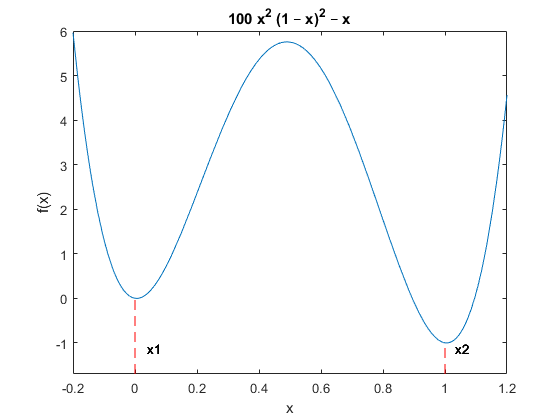
Минимумы расположены в:
fun = @(x)(100*x^2*(x - 1)^2 - x);
x1 = fminbnd(fun,-0.1,0.1)
x1 =
0.0051
x2 = fminbnd(fun,0.9,1.1)
x2 =
1.0049Описание условий
| Термин | Значение |
|---|---|
| Одно локальное решение | Найдите одно локальное решение, точка x, где целевая функция f (x) является локальным минимумом. Для получения дополнительной информации смотрите Локальный по сравнению с Глобальными оптимумами. В примере, обоих x1 и x2 локальные решения. |
| Несколько локальных решений | Найдите набор локальных решений. В примере полным набором локальных решений является {x1,x2}. |
| Одно глобальное решение | Найдите точку x, где целевая функция f (x) является глобальным минимумом. В примере глобальным решением является x2. |
Попробуйте GlobalSearch сначала. Это больше всего фокусируется на нахождении глобального решения и имеет эффективный локальный решатель, fmincon.
Попробуйте MultiStart затем. Это имеет эффективные локальные решатели и может искать большое разнообразие стартовых точек.
Попробуйте patternsearch затем. Это менее эффективно, поскольку это не использует градиенты. Однако patternsearch устойчиво и более эффективен, чем остающиеся локальные решатели, Чтобы искать глобальное решение, запустить patternsearch от множества стартовых точек.
Попробуйте surrogateopt затем. surrogateopt попытки найти глобальное решение с помощью наименьшего количества оценок целевой функции. surrogateopt имеет больше служебное на вычисление функции, чем большинство других решателей. surrogateopt требует конечных границ и принимает и целочисленные ограничения и нелинейные ограничения неравенства.
Попробуйте particleswarm затем, если ваша проблема неограничена или только связала ограничения. Обычно, particleswarm более эффективно, чем остающиеся решатели и может быть более эффективным, чем patternsearch.
Попробуйте ga затем. Это может обработать все типы ограничений и обычно более эффективно, чем simulannealbnd.
Попробуйте simulannealbnd в последний раз. Это может решить проблемы без ограничений или связанных ограничений. simulannealbnd обычно наименее эффективный решатель. Однако, учитывая достаточно медленное расписание охлаждения, это может найти глобальное решение.
GlobalSearch и MultiStart оба предоставляют несколько локальных решений. Для синтаксиса, чтобы получить несколько решений, смотрите Несколько Решений. GlobalSearch и MultiStart отличайтесь по следующим характеристикам:
MultiStart может найти больше локальных минимумов. Это вызвано тем, что GlobalSearch отклонения много сгенерированных стартовых точек (начальная буква указывает для локального решения). По существу, GlobalSearch принимает стартовую точку только, когда она решает, что точка имеет хороший шанс получения глобального минимума. В отличие от этого MultiStart передачи все сгенерированные стартовые точки к локальному решателю. Для получения дополнительной информации см. Алгоритм GlobalSearch.
MultiStart предлагает выбор локального решателя: fmincon, fminunc, lsqcurvefit, или lsqnonlin. GlobalSearch решатель использует только fmincon как его локальный решатель.
GlobalSearch использует поля точек алгоритм поиска в генерации стартовых точек. В отличие от этого MultiStart генерирует точки однородно наугад внутри границ или позволяет вам обеспечивать свои собственные точки.
MultiStart может запуститься параллельно. Смотрите, Как Использовать Параллельную обработку в Global Optimization Toolbox.
Выберите применимый решатель с самым низким номером. Для проблем с целочисленными ограничениями используйте ga.
Используйте fminbnd сначала на одномерных ограниченных задачах только. fminbnd доказуемо сходится быстро в одной размерности.
Используйте patternsearch на любом другом типе проблемы. patternsearch доказуемо сходится и обрабатывает все типы ограничений.
Попробуйте surrogateopt для проблем, которые имеют длительные целевые функции. surrogateopt поиски глобального решения. surrogateopt требует конечных границ и принимает и целочисленные ограничения и нелинейные ограничения неравенства.
Попробуйте fminsearch затем для низко-размерных неограниченных проблем. fminsearch не является столь же общим как patternsearch и может не сходиться. Для низко-размерных проблем, fminsearch прост в использовании, поскольку это имеет немного настраивающихся опций.
Попробуйте particleswarm затем на неограниченных или связано ограниченных проблемах. particleswarm имеет мало теории поддержки, но часто эффективный алгоритм.
Попробуйте ga затем. ga имеет мало теории поддержки и часто менее эффективен, чем patternsearch или particleswarm. ga указатели все типы ограничений. ga и surrogateopt единственные решатели Global Optimization Toolbox, которые принимают целочисленные ограничения.
Попробуйте simulannealbnd в последний раз для неограниченных проблем, или для проблем с границами. simulannealbnd доказуемо сходится только для логарифмического расписания охлаждения, которое является чрезвычайно медленным. simulannealbnd берет только связанные ограничения и часто менее эффективен, чем ga.
| Решатель | Сходимость | Характеристики |
|---|---|---|
GlobalSearch | Быстрая сходимость к локальным оптимумам для сглаженных проблем | Детерминированный выполняет итерации |
| Основанный на градиенте | ||
| Автоматические стохастические стартовые точки | ||
| Удаляет много стартовых точек эвристическим образом | ||
MultiStart | Быстрая сходимость к локальным оптимумам для сглаженных проблем | Детерминированный выполняет итерации |
| Может запуститься параллельно; смотрите, Как Использовать Параллельную обработку в Global Optimization Toolbox | ||
| Основанный на градиенте | ||
| Стохастические или детерминированные стартовые точки или комбинация обоих | ||
| Автоматические стохастические стартовые точки | ||
| Запуски все стартовые точки | ||
Выбор локального решателя: fmincon, fminunc, lsqcurvefit, или lsqnonlin | ||
patternsearch | Доказанная сходимость к локальному оптимуму; медленнее, чем основанные на градиенте решатели | Детерминированный выполняет итерации |
| Может запуститься параллельно; смотрите, Как Использовать Параллельную обработку в Global Optimization Toolbox | ||
| Никакие градиенты | ||
| Предоставленная пользователями стартовая точка | ||
surrogateopt | Доказанная сходимость к глобальному оптимуму для ограниченных задач; медленнее, чем основанные на градиенте решатели; обычно заходит в достижение предела вычисления функции или другого предела | Стохастический выполняет итерации |
| Может запуститься параллельно; смотрите, Как Использовать Параллельную обработку в Global Optimization Toolbox | ||
| Лучше всего используемый в длительных целевых функциях | ||
| Требует связанных ограничений, принимает нелинейные ограничения неравенства | ||
| Позволяет целочисленные ограничения; смотрите Смешано-целочисленную Суррогатную Оптимизацию | ||
| Никакие градиенты | ||
| Автоматические стартовые точки или предоставленные пользователями точки или комбинация обоих | ||
particleswarm | Никакое доказательство сходимости | Стохастический выполняет итерации |
| Может запуститься параллельно; смотрите, Как Использовать Параллельную обработку в Global Optimization Toolbox | ||
| Основанный на населении | ||
| Никакие градиенты | ||
| Автоматическое население запуска или предоставленное пользователями население или комбинация обоих | ||
| Только связанные ограничения | ||
ga | Никакое доказательство сходимости | Стохастический выполняет итерации |
| Может запуститься параллельно; смотрите, Как Использовать Параллельную обработку в Global Optimization Toolbox | ||
| Основанный на населении | ||
| Никакие градиенты | ||
| Позволяет целочисленные ограничения; смотрите Смешанное Целое число ga Оптимизация | ||
| Автоматическое население запуска или предоставленное пользователями население или комбинация обоих | ||
simulannealbnd | Доказанный сходиться к глобальному оптимуму для ограниченных задач с очень медленным расписанием охлаждения | Стохастический выполняет итерации |
| Никакие градиенты | ||
| Предоставленная пользователями стартовая точка | ||
| Только связанные ограничения |
Объяснение некоторых характеристик:
Сходимость — Решатели могут не сходиться ни к какому решению, когда запущено далекому от локального минимума. Когда запущено около локальной переменной минимальные, основанные на градиенте решатели сходятся к локальному минимуму быстро для сглаженных проблем. patternsearch доказуемо сходится для широкого спектра проблем, но сходимость медленнее, чем основанные на градиенте решатели. Оба ga и simulannealbnd может не сходиться за разумное количество времени для некоторых проблем, несмотря на то, что они являются часто эффективными.
Выполняет итерации — Решатели выполняют итерации, чтобы найти решения. Шаги в итерации, выполняет итерации. Некоторые решатели имеют детерминированный, выполняет итерации. Другие используют случайные числа и имеют стохастический, выполняет итерации.
Градиенты — Некоторое использование решателей оцененные или предоставленные пользователями производные в вычислении выполнения итерации. Другие решатели не используют или оценивают производные, но используют только ограничительные значения функции и цель.
Стартовые точки — Большинство решателей требует, чтобы вы обеспечили начальную точку для оптимизации для того, чтобы получить размерность переменных решения. ga и surrogateopt не требуйте никаких начальных точек, потому что они берут размерность переменных решения как вход или выводят размерности из границ. Эти решатели генерируют стартовую точку или население автоматически, или они принимают точку, или указывает, что вы предоставляете.
Сравните характеристики решателей Global Optimization Toolbox к решателям Optimization Toolbox.
| Решатель | Сходимость | Характеристики |
|---|---|---|
fmincon, fminunc, fseminf, lsqcurvefit, lsqnonlin | Доказанная квадратичная сходимость к локальным оптимумам для сглаженных проблем | Детерминированный выполняет итерации |
| Основанный на градиенте | ||
| Предоставленная пользователями начальная точка | ||
fminsearch | Никакое доказательство сходимости — контрпримеры существуют. | Детерминированный выполняет итерации |
| Никакие градиенты | ||
| Предоставленная пользователями стартовая точка | ||
| Никакие ограничения | ||
fminbnd | Доказанная сходимость к локальным оптимумам для сглаженных проблем, медленнее, чем квадратичный. | Детерминированный выполняет итерации |
| Никакие градиенты | ||
| Предоставленный пользователями интервал запуска | ||
| Только одномерные проблемы |
Все эти решатели Optimization Toolbox:
Имейте детерминированный, выполняет итерации
Потребуйте стартовой точки или интервала
Ищите всего одну область притяжения
GlobalSearch и MultiStart объекты. Что это означает для вас?
Вы создаете GlobalSearch или MultiStart объект прежде, чем запустить вашу проблему.
Можно снова использовать объект для выполнения многочисленных проблем.
GlobalSearch и MultiStart объекты являются контейнерами для алгоритмов и глобальных опций. Вы используете эти объекты запустить локальный решатель многократно. Локальный решатель имеет свои собственные опции.
Для получения дополнительной информации смотрите Классы (MATLAB) документация.