Этот пример имеет 2D объективную функцию фитнеса f (x), где x также двумерен:
function f = mymulti1(x) f(1) = x(1)^4 - 10*x(1)^2+x(1)*x(2) + x(2)^4 -(x(1)^2)*(x(2)^2); f(2) = x(2)^4 - (x(1)^2)*(x(2)^2) + x(1)^4 + x(1)*x(2);
Создайте этот файл функции перед продолжением и сохраните его как mymulti1.m на вашем пути MATLAB®.
Чтобы задать задачу оптимизации, запустите приложение Оптимизации и установите его, как изображено.
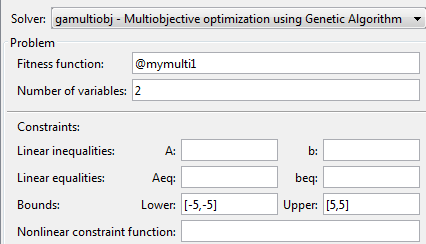
Установите опции для проблемы, как изображено.
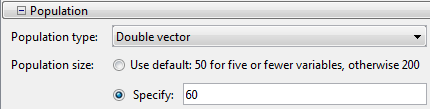
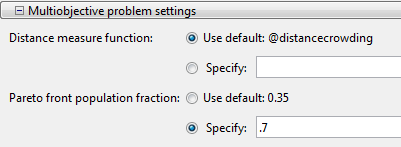
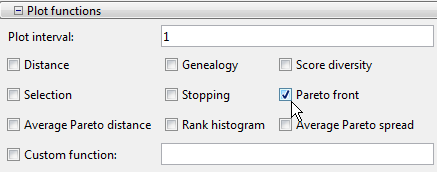
Запустите оптимизацию путем нажатия на Start под Run solver and view results.
График появляется в окне рисунка.
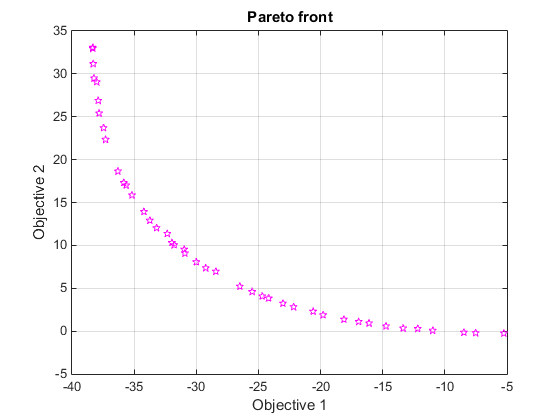
Этот график показывает компромисс между двумя компонентами f. Это построено на пробеле целевой функции; см. рисунок 9-2 фигуры, Набор Ненижних Решений.
Результаты оптимизации появляются в следующей таблице, содержащей и значения целевой функции и значение переменных.
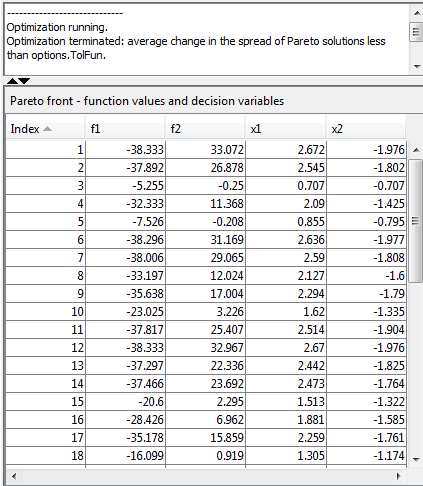
Можно отсортировать таблицу путем нажатия на заголовок. Кликните по заголовку снова, чтобы отсортировать его в обратном порядке. Следующие рисунки показывают результат нажатия на направляющийся f1.
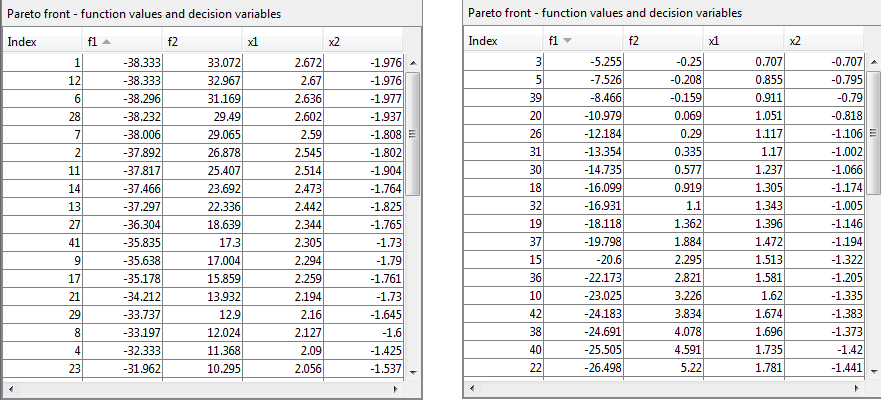
Выполнять ту же оптимизацию в командной строке:
Установите опции:
options = optimoptions('gamultiobj','PopulationSize',60,...
'ParetoFraction',0.7,'PlotFcn',@gaplotpareto);Запустите оптимизацию с помощью опций:
[x,fval,flag,output,population] = gamultiobj(@mymulti1,2,...
[],[],[],[],[-5,-5],[5,5],options);
Существуют другие способы расценить проблему. Следующая фигура содержит график кривых уровня этих двух целевых функций, граница Парето, вычисленная gamultiobj (поля) и x-значения истинной границы Парето (ромбы, соединенные почти-прямой-линией). Истинные пограничные точки Парето - то, где кривые уровня целевых функций параллельны. Они были вычислены путем нахождения, где градиенты целевых функций параллельны. Фигура построена в пространстве параметров; см. рисунок 9-1 фигуры, Сопоставляющий от Пространства параметров в Пробел Целевой функции.
Контуры целевых функций и граница Парето
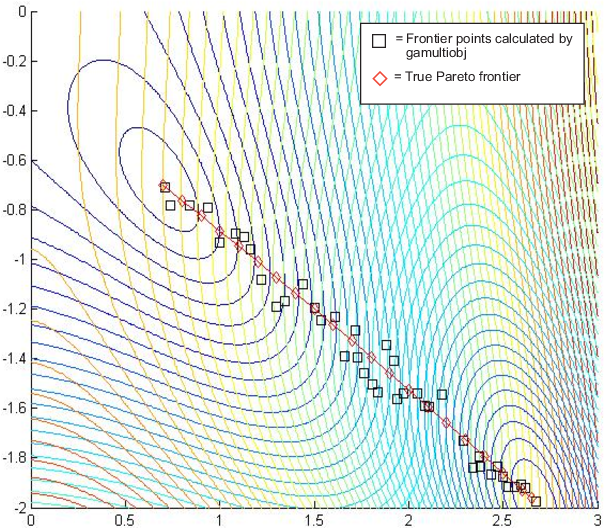
gamultiobj найденный концами линейного сегмента, означая его нашел в полной мере границу Парето.