paretosearch Алгоритмparetosearch Обзор алгоритмаparetosearch алгоритм использует поиск шаблона на наборе точек, чтобы искать итеративно точки, над которыми не доминируют. Смотрите Многоцелевую Терминологию. Поиск шаблона удовлетворяет всем границам и линейным ограничениям в каждой итерации.
Теоретически, алгоритм сходится к точкам около истинной передней стороны Парето. Для обсуждения и доказательства сходимости, смотрите Custòdio и др. [1], чье доказательство применяется к проблемам с Липшицевыми непрерывными целями и ограничениями.
paretosearch Алгоритмparetosearch использование много промежуточных количеств и допусков в его алгоритме.
| Количество | Определение |
|---|---|
| Ранг | Ранг точки имеет итеративное определение.
|
| Объем | Гиперобъем набора точек p на пробеле целевой функции, которые удовлетворяют неравенству для каждого индекса j, fi (j) <pi <Mi, где fi (j) является i th компонент j th значение целевой функции во Множестве Парето, и Mi является верхней границей для i th компонент для всех точек во Множестве Парето. В этом рисунке M называется Контрольной точкой. Оттенки серого в фигуре обозначают фрагменты объема, который некоторые алгоритмы расчета используют в качестве части вычисления исключения включения.
Для получения дополнительной информации смотрите Флейшера [3].
Изменение объема, каждый включает остановку алгоритма. Для получения дополнительной информации смотрите Останавливающиеся Условия. |
| Расстояние | Расстояние является мерой близости индивидуума ее самым близким соседям. Алгоритм устанавливает расстояние индивидуумов в крайних положениях к
Алгоритм сортирует каждую размерность отдельно, таким образом, термин neighbors означает соседей в каждой размерности. У индивидуумов того же ранга с более высоким расстоянием есть более высокий шанс выбора (более высокое расстояние лучше). Расстояние, каждый включает вычисление распространения, которое является частью останавливающегося критерия. Для получения дополнительной информации смотрите Останавливающиеся Условия. |
| Распространение | Распространение является мерой перемещения Множества Парето. Вычислить распространение,
Распространение мало, когда экстремальные значения целевой функции не изменяются очень между итерациями (то есть, μ мал), и когда точки на передней стороне Парето распространены равномерно (то есть, σ мал).
|
ParetoSetChangeTolerance | Остановка условия для поиска. paretosearch остановки, когда объем, распространение или расстояние не изменяются больше, чем ParetoSetChangeTolerance по окну итераций. Для получения дополнительной информации смотрите Останавливающиеся Условия. |
MinPollFraction | Минимальная часть местоположений, чтобы опросить во время итерации. Эта опция не применяется когда |
paretosearch Алгоритм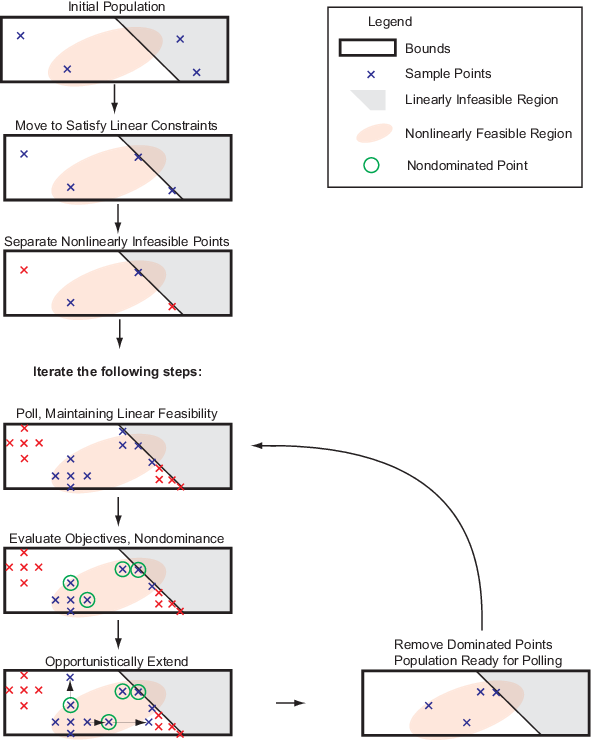
Создать начальный набор точек, paretosearch генерирует options.ParetoSetSize точки от квазислучайной выборки на основе проблемных границ, по умолчанию. Для получения дополнительной информации смотрите Bratley и Fox [2]. Когда проблема имеет более чем 500 размерностей, paretosearch латинская выборка гиперкуба использования, чтобы сгенерировать начальные точки.
Если компонент не имеет никаких границ, paretosearch использует искусственную нижнюю границу -10 и искусственная верхняя граница 10.
Если компонент имеет только один связанный, paretosearch использование, которое связало как конечная точка интервала ширины 20 + 2*abs(bound). Например, если нет никакой верхней границы для компонента и существует нижняя граница 15, paretosearch использует ширину интервала 20 + 2*15 = 55, так использует искусственную верхнюю границу 15 + 55 = 70.
Если вы передаете некоторые начальные точки в options.InitialPoints, затем paretosearch использование те точки как начальная буква указывает. paretosearch генерирует больше точек, при необходимости, чтобы получить, по крайней мере, options.ParetoSetSize начальные точки.
paretosearch затем проверяет, что начальная буква указывает, чтобы гарантировать, что они выполнимы относительно границ и линейных ограничений. При необходимости, paretosearch проектирует начальные точки на линейное подпространство линейно допустимых точек путем решения задачи линейного программирования. Этот процесс может заставить некоторые точки совпадать, в этом случае paretosearch удаляет любые дублирующиеся точки. paretosearch не изменяет начальные точки для искусственных границ, только для заданных границ и линейных ограничений.
После перемещения точек, чтобы удовлетворить линейным ограничениям, при необходимости, paretosearch проверки, удовлетворяют ли точки нелинейным ограничениям. paretosearch дает значение штрафа Inf к любой точке, которая не удовлетворяет всем нелинейным ограничениям. Затем paretosearch вычисляет любые недостающие значения целевой функции остающихся допустимых точек.
В настоящее время, paretosearch не поддерживает нелинейные ограничения равенства ceq(x) = 0.
paretosearch обеспечивает два набора точек:
archive — Структура, которая содержит точки, над которыми не доминируют, сопоставленные с размером mesh ниже options.MeshTolerance и удовлетворение всем ограничениям к в options.ConstraintTolerance. archive структура содержит не больше, чем 2*options.ParetoSetSize точки и первоначально пусты. Каждая точка в archive содержит связанный размер mesh, который является размером mesh, в котором была сгенерирована точка.
iterates — Структура, содержащая точки, над которыми не доминируют, и возможно некоторые точки, над которыми доминируют, сопоставленные с большими размерами mesh или недопустимостью. Каждая точка в iterates содержит связанный размер mesh. iterates содержит не больше, чем options.ParetoSetSize 'points'.
paretosearch опросы указывают от iterates, с опрошенными точками, наследовавшими связанный размер mesh от точки в iterates. paretosearch алгоритм использует опрос, который обеспечивает выполнимость относительно границ и всех линейных ограничений.
Если проблема имеет нелинейные ограничения, paretosearch вычисляет выполнимость каждой точки опроса. paretosearch сохраняет счет неосуществимых точек отдельно от счета допустимых точек. Счет допустимой точки является вектором значений целевой функции той точки. Счет неосуществимой точки является суммой нелинейного infeasibilities.
paretosearch опросы, по крайней мере, MinPollFraction* (число точек в шаблоне) местоположения для каждой точки в iterates. Если опрошенные точки дают по крайней мере одну точку, над которой не доминируют, относительно действующей (исходной) точки, опрос рассматривается успехом. В противном случае, paretosearch продолжает опрашивать до него или находит точку, над которой не доминируют, или исчерпывает точки в шаблоне. Если paretosearch исчерпывает точки и не производит точку, над которой не доминируют, paretosearch объявляет неудачный опрос и половины размер mesh.
Если опрос находит точки, над которыми не доминируют, paretosearch расширяет опрос в успешных направлениях неоднократно, удваивая размер mesh каждый раз, пока расширение не производит точку, над которой доминируют. Во время этого расширения, если размер mesh превышает options.MaxMeshSize (значение по умолчанию: Inf), остановки опроса. Если значения целевой функции уменьшаются к -Inf, paretosearch объявляет неограниченную проблему и остановки.
archive и iterates СтруктурыПосле опроса всех точек в iterates, алгоритм исследует новые точки вместе с точками в iterates и archive структуры. paretosearch вычисляет ранг или передний номер Парето, каждой точки и затем делает следующее.
Отметьте для удаления все точки, которые не имеют ранга 1 в archive.
Отметьте новый ранг 1 точки для вставки в iterates.
Отметьте допустимые точки в iterates чей связанный размер mesh меньше options.MeshTolerance для передачи в archive.
Отметьте точки, над которыми доминируют, в iterates для удаления, только если они препятствуют тому, чтобы новые точки, над которыми не доминируют, были добавлены к iterates.
paretosearch затем вычисляет объем и меры по расстоянию для каждой точки. Если archive переполнится в результате отмеченных включаемых точек, затем точки с самым большим объемом занимают archive, и другие уезжают. Точно так же новые точки, отмеченные для добавления к iterates введите iterates в порядке их объемов.
Если iterates полно и не имеет никаких точек, над которыми доминируют, затем paretosearch не добавляют никакие точки к iterates и объявляет, что итерация неудачна. paretosearch умножает размеры mesh в iterates 1/2.
Для трех или меньшего количества целевых функций, paretosearch объем использования и распространение как останавливающиеся меры. Для четырех или больше целей, paretosearch расстояние использования и распространение как останавливающиеся меры. В остатке от этого обсуждения, две меры, что paretosearch использование обозначается меры applicable.
Алгоритм обеспечивает векторы последних восьми значений применимых мер. После восьми итераций алгоритм проверяет значения двух применимых мер в начале каждой итерации, где tol = options.ParetoSetChangeTolerance:
spreadConverged = abs(spread(end - 1) - spread(end)) <= tol*max(1,spread(end - 1));
volumeConverged = abs(volume(end - 1) - volume(end)) <= tol*max(1,volume(end - 1));
distanceConverged = abs(distance(end - 1) - distance(end)) <= tol*max(1,distance(end - 1));
Если любым применимым тестом является true, остановки алгоритма. В противном случае алгоритм вычисляет макс. из условий в квадрате преобразований Фурье применимых мер минус первый срок. Алгоритм затем сравнивает максимумы с их удаленными условиями (компоненты DC преобразований). Если любой удаленный термин больше, чем 100*tol*(max of all other terms), затем остановки алгоритма. Этот тест по существу решает, что последовательность мер не колеблется, и поэтому сходилась.
Кроме того, функция построения графика или выходная функция могут остановить алгоритм, или алгоритм может остановиться, потому что это превышает предел вычисления функции или ограничение по времени.
Алгоритм возвращает точки на передней стороне Парето можно следующим образом.
paretosearch комбинирует точки в archive и iterates в один набор.
Когда существует три или меньше целевых функций, paretosearch возвращает точки от самого большого объема до самого маленького, до в большей части ParetoSetSize 'points'.
Когда существует четыре или больше целевых функции, paretosearch возвращает точки от самого большого расстояния до самого маленького, до в большей части ParetoSetSize 'points'.
Когда paretosearch вычисляет значения целевой функции параллельно или векторизованным способом (UseParallel true или UseVectorized true), существуют некоторые изменения в алгоритме.
Когда UseVectorized true, paretosearch игнорирует MinPollFraction опция и оценивает все точки опроса в шаблоне.
При вычислении параллельно, paretosearch последовательно исследует каждую точку в iterates и выполняет параллельный опрос от каждой точки. После возврата MinPollFraction часть точек опроса, paretosearch определяет, доминируют ли какие-либо точки опроса над базисной точкой. Если так, опрос считают успешным, и любой другой параллельный останов оценок. В противном случае опрос продолжается, пока точка доминирования не появляется, или опрос сделан.
paretosearch выполняет оценки целевой функции или на рабочих или векторизованным способом, но не обоими. Если вы устанавливаете оба UseParallel и UseVectorized к true, paretosearch вычисляет значения целевой функции параллельно на рабочих, но не векторизованным способом. В этом случае, paretosearch игнорирует MinPollFraction опция и оценивает все точки опроса в шаблоне.
paretosearch БыстроСамый быстрый способ запустить paretosearch зависит от нескольких факторов.
Если оценки целевой функции являются медленными, то это является обычно самым быстрым, чтобы использовать параллельные вычисления. Издержки в параллельных вычислениях могут быть существенными, когда оценки целевой функции быстры, но когда они являются медленными, обычно лучше использовать больше вычислительной мощности.
Параллельные вычисления требуют лицензии Parallel Computing Toolbox™.
Если оценки целевой функции не являются очень трудоемкими, то это является обычно самым быстрым, чтобы использовать векторизованную оценку. Однако это не всегда имеет место, потому что векторизованные расчеты оценивают целый шаблон, тогда как последовательные оценки могут взять только небольшую часть шаблона. В высоких размерностях особенно, это сокращение оценок может заставить последовательную оценку быть быстрее для некоторых проблем.
Чтобы использовать векторизованное вычисление, ваша целевая функция должна принять матрицу с произвольным числом строк. Каждая строка представляет одну точку, чтобы оценить. Целевая функция должна возвратить матрицу значений целевой функции с одинаковым числом строк, как это принимает с одним столбцом для каждой целевой функции. Для одно-объективного обсуждения смотрите, Векторизуют Функцию Фитнеса (ga) или векторизованная целевая функция (patternsearch).
[1] Custòdio, A. L. Дж. Ф. А. Мэдейра, А. Ай. Ф. Вэз и Л. Н. Висенте. Прямой Мультипоиск Многоцелевой Оптимизации. SIAM J. Optim., 21 (3), 2011, стр 1109–1140. Предварительная печать, доступная в https://estudogeral.sib.uc.pt/bitstream/10316/13698/1/Direct%20multisearch%20for%20multiobjective%20optimization.pdf.
[2] Bratley, P. и Б. Л. Фокс. Алгоритм 659: Реализация квазислучайного генератора последовательности Собола. Математика Сделки ACM. Программное обеспечение 14, 1988, стр 88–100.
[3] Флейшер, M. Мера Парето Optima: Приложения к Многоцелевой Метаэвристике. В "Продолжениях Второй Международной конференции по вопросам Эволюционной Оптимизации Мультикритерия — EMO" апрель 2003 в Фару, Португалия. Опубликованный Springer-Verlag в серии Lecture Notes in Computer Science, Издании 2632, стр 519–533. Предварительная печать, доступная в http://www.dtic.mil/get-tr-doc/pdf? AD=ADA441037.