Как пример, рассмотрите следующую функцию.
Следующий рисунок показывает график функции.
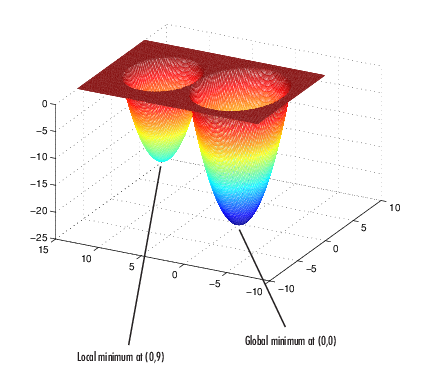
Глобальный минимум функции происходит в (0, 0), где ее значение-25. Однако функция также имеет локальный минимум в (0, 9), где его значение-16.
Создать файл, который вычисляет функцию, копию и вставляет следующий код в новый файл в Редакторе MATLAB®.
function z = poll_example(x) if x(1)^2 + x(2)^2 <= 25 z = x(1)^2 + x(2)^2 - 25; elseif x(1)^2 + (x(2) - 9)^2 <= 16 z = x(1)^2 + (x(2) - 9)^2 - 16; else z = 0; end
Затем сохраните файл как poll_example.m в папке на пути MATLAB.
Чтобы запустить поиск шаблона на функции, введите следующее в приложение Оптимизации:
Установите Solver на patternsearch.
Установите Objective function на @poll_example.
Установите Start point на [0 5].
Установите Level of display на Iterative в опциях Display to command window.
Нажмите Start, чтобы запустить поиск шаблона с набором Complete poll к Off, его значение по умолчанию.
В качестве альтернативы запускать эту проблему с помощью функций командной строки:
options = optimoptions('patternsearch','Display','iter'); [x,fval] = patternsearch(@poll_example,[0,5],... [],[],[],[],[],[],[],options);
Отображения приложения Оптимизации результаты в панели Run solver and view results, как показано в следующем рисунке.
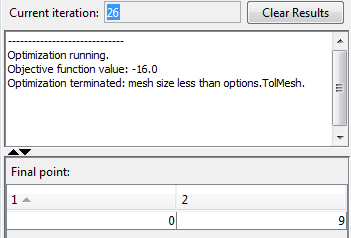
Поиск шаблона возвращает локальный минимум в (0, 9). В начальной точке, (0, 5), значение целевой функции 0. В первой итерации поиск опрашивает следующие точки mesh.
f ((0, 5) + (1, 0)) = f (1, 5) = 0
f ((0, 5) + (0, 1)) = f (0, 6) = -7
Как только поиск опрашивает точку mesh (0, 6), в котором значение целевой функции меньше в начальной точке, это прекращает опрашивать текущую mesh и устанавливает текущую точку в следующей итерации к (0, 6). Следовательно, поиск перемещается к локальному минимуму в (0, 9) в первой итерации. Вы видите это путем рассмотрения первых двух линий отображения командной строки.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 3 -7 2 Successful PollОбратите внимание на то, что поиск шаблона выполняет только две оценки целевой функции при первой итерации, увеличивая общее функциональное количество от 1 до 3.
Затем установите Complete poll на On и нажмите Start. В качестве альтернативы в командной строке:
options.UseCompletePoll = true;
[x,fval] = patternsearch(@poll_example,[0,5],...
[],[],[],[],[],[],[],options);Панель Run solver and view results отображает следующие результаты.
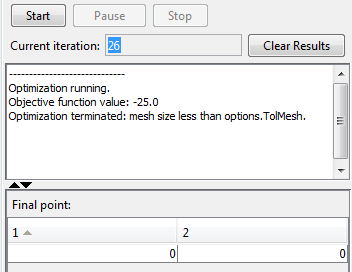
На этот раз поиск шаблона находит глобальный минимум в (0, 0). Различие между этим запуском и предыдущим - то, который с Complete poll установил на On, в первой итерации поиск шаблона опрашивает все четыре точки mesh.
f ((0, 5) + (1, 0)) = f (1, 5) = 0
f ((0, 5) + (0, 1)) = f (0, 6) = -6
f ((0, 5) + (-1, 0)) = f (-1, 5) = 0
f ((0, 5) + (0, -1)) = f (0, 4) = -9
Поскольку последняя точка mesh имеет самое низкое значение целевой функции, поиск шаблона выбирает его как текущую точку в следующей итерации. Первые две линии отображения командной строки показывают это.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 5 -9 2 Successful PollВ этом случае целевая функция выполнена четыре раза в первой итерации. В результате шаблон ищет перемещения к глобальному минимуму в (0, 0).
Следующая фигура сравнивает последовательность точек, возвращенных, когда Complete poll установлен в Off с последовательностью, когда Complete poll является On.
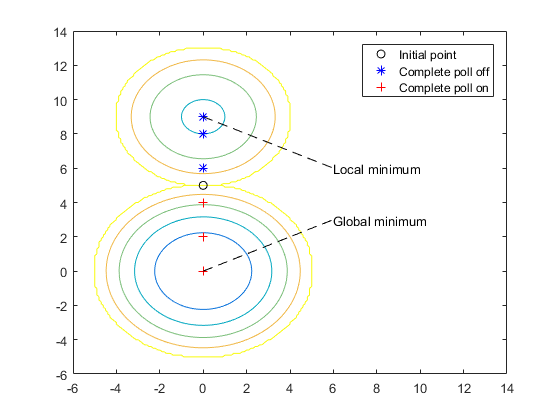
В этом примере показано, как несколько опций опроса взаимодействуют в терминах итераций и общих вычислений функции. Основные результаты:
GSS более эффективен, чем GPS или MADS для линейно ограниченных проблем.
Ли установка UseCompletePoll к true КПД увеличений или КПД уменьшений неясны, несмотря на то, что это влияет на количество итераций.
Точно так же, ли наличие 2N опрос более или менее эффективен, чем наличие Np1 опрос также неясен. Самым эффективным опросом является GSS Positive Basis Np1 с набором Complete poll к on. Наименее эффективным является MADS Positive Basis Np1 с набором Complete poll к on.
КПД алгоритма зависит от проблемы. GSS эффективен для линейно ограниченных проблем. Однако предсказание последствий КПД других опций опроса затрудняет, как знает, какой тип опроса работает лучше всего с другими ограничениями.
Проблема эквивалентна в Выполнении Поиска Шаблона на Примере. Эта линейно ограниченная проблема использует lincontest7 файл, который идет с тулбоксом:
Введите следующее в свое рабочее пространство MATLAB:
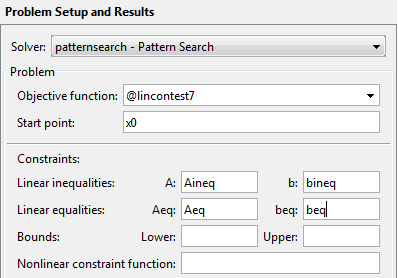
x0 = [2 1 0 9 1 0]; Aineq = [-8 7 3 -4 9 0]; bineq = 7; Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3]; beq = [84 62 65 1];
Откройте приложение Оптимизации путем ввода optimtool в командной строке.
Выберите patternsearch решатель.
Введите проблему и ограничения, как изображено.
Убедитесь, что Poll method является GPS Positive basis 2N.
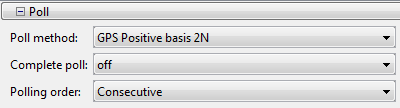
Запустите оптимизацию.
Выберите File > Export to Workspace.
Экспортируйте результаты и назовите их gps2noff.
Установите Options > Poll > Complete poll на on.
Запустите оптимизацию.
Экспортируйте результат и назовите его gps2non.
Установите Options > Poll > Poll method на GPS Positive basis Np1 и набор Complete poll к off.
Запустите оптимизацию.
Экспортируйте результат и назовите его gpsnp1off.
Установите Complete poll на on.
Запустите оптимизацию.
Экспортируйте результат и назовите его gpsnp1on.
Продолжите подобным способом создавать структуры решения для других методов опроса с набором Complete poll on и off: gss2noff, gss2non, gssnp1off, gssnp1on, mads2noff, mads2non, madsnp1off, и madsnp1on.
В качестве альтернативы можно сгенерировать результаты, описанные в, Генерируют Результаты в командной строке.
Установите первоначальные опции и целевую функцию.
options = optimoptions('patternsearch',...
'PollMethod','GPSPositiveBasis2N',...
'PollOrderAlgorithm','consecutive',...
'UseCompletePoll',false);
fun = @lincontest7;Запустите оптимизацию, назвав output структура outputgps2noff.
[x,fval,exitflag,outputgps2noff] = patternsearch(fun,x0,...
Aineq,bineq,Aeq,beq,[],[],[],options);Установите опции использовать полный опрос.
options.UseCompletePoll = true;
Запустите оптимизацию, назвав output структура outputgps2non.
[x,fval,exitflag,outputgps2non] = patternsearch(fun,x0,...
Aineq,bineq,Aeq,beq,[],[],[],options);Установите опции использовать 'GPSPositiveBasisNp1' опросите метод а не использовать полный опрос.
options.PollMethod = 'GPSPositiveBasisNp1'; options.UseCompletePoll = false;
Запустите оптимизацию, назвав output структура outputgps2np1off.
[x,fval,exitflag,outputgps2np1off] = patternsearch(fun,x0,...
Aineq,bineq,Aeq,beq,[],[],[],options);Продолжите подобным способом создавать структуры output для других методов опроса с UseCompletePoll установите true и false: outputgss2noff, outputgss2non, outputgssnp1off, outputgssnp1on, outputmads2noff, outputmads2non, outputmadsnp1off, и outputmadsnp1on.
У вас есть результаты 12 запусков оптимизации. Следующая таблица показывает КПД запусков, измеренных в общих функциональных количествах и в итерациях. Ваши результаты MADS могли отличаться, поскольку MADS является стохастическим алгоритмом.
| Алгоритм | Функциональное количество | Итерации |
|---|---|---|
| GPS2N, полный опрос прочь | 1462 | 136 |
| GPS2N, полный опрос на | 1396 | 96 |
| GPSNp1, полный опрос прочь | 864 | 118 |
| GPSNp1, полный опрос на | 1007 | 104 |
| GSS2N, полный опрос прочь | 758 | 84 |
| GSS2N, полный опрос на | 889 | 74 |
| GSSNp1, полный опрос прочь | 533 | 94 |
| GSSNp1, полный опрос на | 491 | 70 |
| MADS2N, полный опрос прочь | 922 | 162 |
| MADS2N, полный опрос на | 2285 | 273 |
| MADSNp1, полный опрос прочь | 1155 | 201 |
| MADSNp1, полный опрос на | 1651 | 201 |
Чтобы получить, скажем, первую строку в таблице, введите gps2noff.output.funccount и gps2noff.output.iterations. Можно также исследовать опции в редакторе Переменных путем двойного клика по опциям в Браузере Рабочей области, и затем двойного клика по output структура.
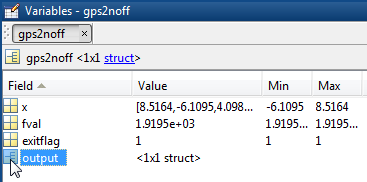
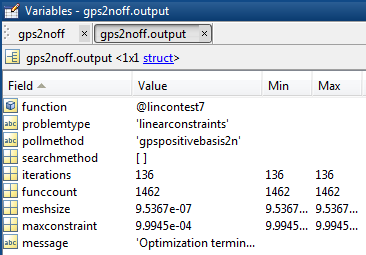
В качестве альтернативы, если вы запустили проблемы в командной строке, можно получить доступ к данным из структур output.
[outputgps2noff.funccount,outputgps2noff.iterations]
ans =
1462 136Основные результаты, подбираемые из таблицы:
Установка Complete poll к on обычно понижает количество итераций для GPS и GSS, но изменение в количестве вычислений функции непредсказуемо.
Установка Complete poll к on не обязательно изменяет количество итераций для MADS, но существенно увеличивает число вычислений функции.
Самые эффективные настройки алгоритма/опций, с КПД, означающим самое низкое функциональное количество:
GSS Positive basis Np1 с набором Complete poll к on (функциональное количество 491)
GSS Positive basis Np1 с набором Complete poll к off (функциональное количество 533)
GSS Positive basis 2N с набором Complete poll к off (функциональное количество 758)
GSS Positive basis 2N с набором Complete poll к on (функциональное количество 889)
Другие методы опроса имели функциональные количества, превышающие 900.
Для этой проблемы самым эффективным опросом является GSS Positive Basis Np1 с набором Complete poll к on, несмотря на то, что установка Complete poll имеет только небольшое значение. Наименее эффективным опросом является MADS Positive Basis 2N с набором Complete poll к on. В этом случае установка Complete poll имеет существенное значение.