Радон преобразовывает

Примечание

Для получения информации о создании данных о проекции из линейных интегралов вдоль путей, которые исходят из одного источника, названного проекциями луча вентилятора, смотрите Проекцию Луча Вентилятора. Чтобы преобразовать данные о проекции параллельного луча в данные о проекции луча вентилятора, используйте para2fan функция.

radon функция вычисляет проекции матрицы изображений вдоль заданных направлений.

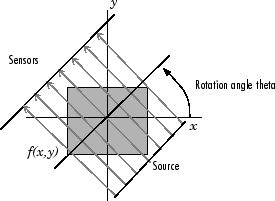
Проекция двумерной функции f (x, y) является набором линейных интегралов. radon функция вычисляет линейные интегралы от многочисленных источников вдоль параллельных путей или лучи, в определенном направлении. Лучи расположены модуль на 1 пиксель с интервалами независимо. Представлять изображение, radon функционируйте берет несколько, проекции параллельного луча изображения от различных углов путем вращения источника вокруг центра изображения. Следующий рисунок показывает одну проекцию при заданном угле поворота.

Проекция параллельного луча в тете угла поворота

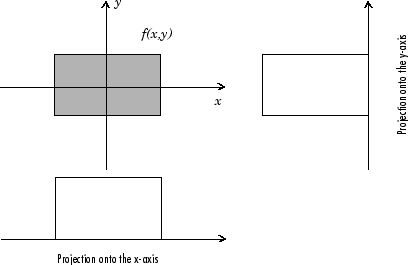
Например, линейный интеграл f (x, y) в вертикальном направлении является проекцией f (x, y) на ось X; линейный интеграл в горизонтальном направлении является проекцией f (x, y) на ось Y. Следующий рисунок показывает горизонтальные и вертикальные проекции для простой двумерной функции.

Горизонтальные и вертикальные проекции простой функции

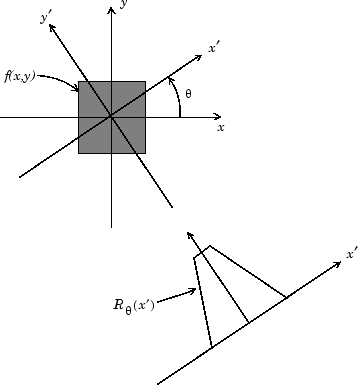
Проекции могут быть вычислены вдоль любого угла theta (θ). В общем случае преобразование Радона f (x, y) является линейным интегралом f, параллельного y '-оси

$R_{θ} (x') = \int_{- \infty}^{\infty} f (x' \cos θ - y' \sin θ, x' \sin θ + y' \cos θ) d y'$

где

$[\begin{matrix} x' \\ y' \end{matrix}] = [\begin{matrix} \cos θ & sin θ \\ - \sin θ & потому что θ \end{matrix}] [\begin{matrix} x \\ y \end{matrix}]$

Следующая фигура иллюстрирует, что геометрия Радона преобразовывает.

Геометрия радона преобразовывает

Постройте преобразование радона изображения

Скрипт Open Live Script

В этом примере показано, как вычислить преобразование Радона изображения, I, для определенного набора углов, theta, использование radon функция. Функция возвращается, R, в котором столбцы содержат Радон, преобразовывают для каждого угла в theta. Функция также возвращает вектор, xp , который содержит соответствующие координаты вдоль оси X. Центральный пиксель I задан, чтобы быть floor((size(I)+1)/2), который является пикселем на оси X, соответствующей x' = 0.

Создайте изображение небольшой выборки для этого примера, который состоит из одного квадратного объекта, и отобразите его.

I = zeros(100,100);
I(25:75,25:75) = 1;
imshow(I)

Вычислите преобразование Радона изображения для углов 0 градусов и 45 градусов.

[R,xp] = radon(I,[0 45]);

Постройте преобразование для 0 градусов.

figure
plot(xp,R(:,1));
title('Radon Transform of a Square Function at 0 degrees')

Постройте преобразование для 45 градусов.

figure
plot(xp,R(:,2)); 
title('Radon Transform of a Square Function at 45 degrees')

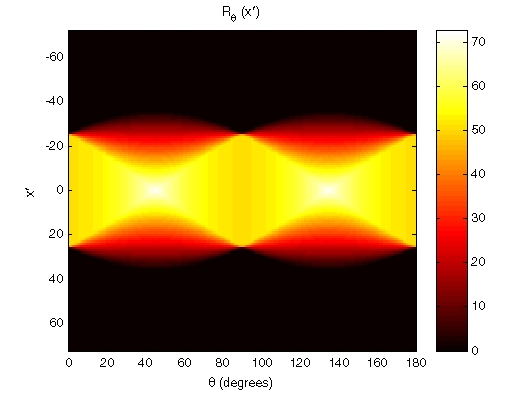
Просмотр радона преобразовывает как изображение

Радон преобразовывает для большого количества углов, часто отображается как изображение. В этом примере Радон преобразовывает для квадратного изображения, вычисляется под углами от 0 ° до 180 °, с шагом на 1 °.

theta = 0:180;
[R,xp] = radon(I,theta);
imagesc(theta,xp,R);
title('R_{\theta} (X\prime)');
xlabel('\theta (degrees)');
ylabel('X\prime');
set(gca,'XTick',0:20:180);
colormap(hot);
colorbar

Радон преобразовывает Используя 180 проекций

Документация