Создайте матрицу совместной встречаемости уровня серого из изображения
glcms = graycomatrix(I)I. Другим именем для матрицы совместной встречаемости уровня серого является gray-level spatial dependence matrix.
graycomatrix создает GLCM путем вычисления, как часто пиксель с уровнем серого (полутоновая интенсивность) значение i происходит горизонтально смежный с пикселем со значением j. (Можно задать другие пиксельные пространственные отношения с помощью 'Offsets' параметр.) Каждый элемент (i, j) в glcm задает число раз, что пиксель со значением i произошла горизонтально смежная с пикселем со значением j.
glcms = graycomatrix(I,Name,Value)
Считайте полутоновое изображение в рабочую область.
I = imread('circuit.tif');
imshow(I)
Вычислите матрицу совместной встречаемости уровня серого (GLCM) для полутонового изображения. По умолчанию, graycomatrix вычисляет GLCM на основе горизонтальной близости пикселей: [0 1]. Это - пиксель рядом с пикселем процента по той же строке. Этот пример задает различное смещение: две строки независимо на том же столбце.
glcm = graycomatrix(I,'Offset',[2 0])glcm = 8×8
14205 2107 126 0 0 0 0 0
2242 14052 3555 400 0 0 0 0
191 3579 7341 1505 37 0 0 0
0 683 1446 7184 1368 0 0 0
0 7 116 1502 10256 1124 0 0
0 0 0 2 1153 1435 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
Создайте простое 3 6 демонстрационный массив.
I = [ 1 1 5 6 8 8; 2 3 5 7 0 2; 0 2 3 5 6 7]
I = 3×6
1 1 5 6 8 8
2 3 5 7 0 2
0 2 3 5 6 7
Вычислите матрицу совместной встречаемости уровня серого (GLCM) и возвратите масштабированное изображение, используемое в вычислении. Путем определения пустых скобок для GrayLimits параметр, пример использует минимальные и максимальные полутоновые значения во входном изображении как пределы.
[glcm,SI] = graycomatrix(I,'NumLevels',9,'GrayLimits',[])
glcm = 9×9
0 0 2 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0
0 0 0 2 0 0 0 0 0
0 0 0 0 0 2 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 2 1 0
0 0 0 0 0 0 0 1 1
1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1
SI = 3×6
2 2 6 7 9 9
3 4 6 8 1 3
1 3 4 6 7 8
Считайте полутоновое изображение в рабочую область.
I = imread('cell.tif');
imshow(I)
Задайте четыре смещения.
offsets = [0 1; -1 1;-1 0;-1 -1];
Вычислите GLCMs, возвратив масштабированное изображение также. Отобразите масштабированное изображение, выполнив дополнительное перемасштабирование значений данных к области значений [0, 1].
[glcms,SI] = graycomatrix(I,'Offset',offsets);
imshow(rescale(SI))
Отметьте, как функция возвращает массив четырех GLCMs.
whos
Name Size Bytes Class Attributes I 159x191 30369 uint8 SI 159x191 242952 double glcms 8x8x4 2048 double offsets 4x2 64 double
Считайте полутоновое изображение в рабочую область.
I = imread('circuit.tif');
imshow(I)
Вычислите GLCM использование Symmetric опция, возвращая масштабированное изображение также. GLCM создал, когда вы устанавливаете Symmetric к true симметрично через его диагональ и эквивалентен GLCM, описанному Haralick (1973).
[glcm,SI] = graycomatrix(I,'Offset',[2 0],'Symmetric',true); glcm
glcm = 8×8
28410 4349 317 0 0 0 0 0
4349 28104 7134 1083 7 0 0 0
317 7134 14682 2951 153 0 0 0
0 1083 2951 14368 2870 2 0 0
0 7 153 2870 20512 2277 0 0
0 0 0 2 2277 2870 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
Отобразите масштабированное изображение, выполнив дополнительное перемасштабирование значений данных к области значений [0, 1].
imshow(rescale(SI))
I — Полутоновое изображениеВведите изображение в виде 2D числовой матрицы или 2D логической матрицы.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
'Offset',[2 0]'GrayLimits' — Область значений, используемая, масштабируя вход, отображает на уровни серого[low high] с 2 элементамиОбласть значений, используемая, масштабируя вход, отображает на уровни серого в виде векторного [low high] с 2 элементами. Если N количество уровней серого (см. параметр 'NumLevels') использовать в масштабировании, область значений [low high] разделен на N равные интервалы ширины и значения в интервале сопоставлены с одним уровнем серого. Полутоновые значения, меньше чем или равные low масштабируются к 1. Полутоновые значения, больше, чем или равный high масштабируются к 'NumLevels'. If'GrayLimits' установлен в [], graycomatrix использует минимальные и максимальные полутоновые значения в I как пределы, [min(I(:)) max(I(:))], например, [0 1] поскольку класс удваивается и [-32768 32767] для класса int16.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
'NumLevels' — Количество уровней серогоКоличество уровней серого в виде целого числа. Например, если NumLevels 8, graycomatrix масштабирует значения в I таким образом, они - целые числа между 1 и 8. Количество уровней серого определяет размер матрицы совместной встречаемости уровня серого (glcm).
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
'Offset' — Расстояние между пикселем интереса и его соседомРасстояние между пикселем интереса и его соседом в виде p-by-2 массив целых чисел. Каждая строка в массиве является двухэлементным вектором, [row_offset, col_offset], это задает отношение или смещение, пары пикселей. row_offset количество строк между пикселем интереса и его соседом. col_offset количество столбцов между пикселем интереса и его соседом. Поскольку смещение часто выражается как угол, следующая таблица приводит значения смещения, которые задают общие углы, учитывая пиксельное расстояние D.
\angle | Смещение |
|---|---|
| 0 |
|
| 45 |
|
| 90 | [-D 0] |
| 135 | [-D -D] |
Фигура иллюстрирует массив: offset = [0 1; -1 1; -1 0; -1 -1]
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
'Symmetric' — Рассмотрите упорядоченное расположение значенийfalse (значение по умолчанию) | trueСчитайте упорядоченное расположение значений в виде булева значения true или false. Например, когда 'Symmetric' установлен в true, graycomatrix количества и 1,2 и 2,1 соединения при вычислении числа раз значение 1 смежны со значением 2. Когда 'Symmetric' установлен в false, graycomatrix только количества 1,2 или 2,1, в зависимости от значения 'offset'.
Типы данных: логический
graycomatrix вычисляет GLCM от масштабированной версии изображения. По умолчанию, если I двухуровневое изображение, graycomatrix масштабирует изображение к двум уровням серого. Если I изображение интенсивности, graycomatrix масштабирует изображение к восьми уровням серого. Можно задать количество уровней серого graycomatrix использование, чтобы масштабировать изображение при помощи 'NumLevels' параметр и путь, который graycomatrix масштабирует значения с помощью 'GrayLimits' параметр.
Следующий рисунок показывает как graycomatrix вычисляет несколько значений в GLCM 4 5 изображение I. Элемент (1,1) в GLCM содержит значение 1 потому что существует только один экземпляр в изображении, где два, горизонтально смежные пиксели имеют значения 1 и 1. Элемент (1,2) в GLCM содержит значение 2 потому что существует два экземпляра в изображении, где два, горизонтально смежные пиксели имеют значения 1 и 2. graycomatrix продолжает эту обработку, чтобы заполнить все значения в GLCM.
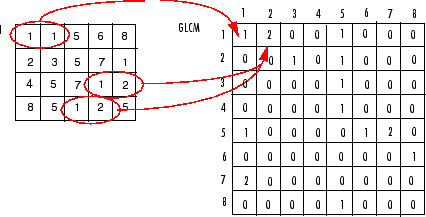
graycomatrix игнорирует пиксельные пары, если любой из пикселей содержит NaN, заменяет положительный Infs со значением NumLevels, и замены отрицательный Infs со значением 1. graycomatrix игнорирует краевые элементы изображения, если соответствующий соседний пиксель выходит за пределы границ изображения.
GLCM, созданный, когда 'Symmetric' установлен в true симметрично через его диагональ и эквивалентен GLCM, описанному Haralick (1973). GLCM производится следующим синтаксисом с 'Symmetric' установите на true
graycomatrix(I, 'offset', [0 1], 'Symmetric', true)
эквивалентно сумме двух GLCMs, произведенных следующими операторами where'Symmetric' установлен в false.
graycomatrix(I, 'offset', [0 1], 'Symmetric', false) graycomatrix(I, 'offset', [0 -1], 'Symmetric', false)
[1] Haralick, R.M., К. Шэнмугэн и я. Динштайн, "Структурные Функции Классификации Изображений", Транзакции IEEE в Системах, Человеке, и Кибернетике, Издании SMC-3, 1973, стр 610-621.
[2] Haralick, R.M., и Л.Г. Шапиро. Компьютер и Видение Робота: Издание 1, Аддисон-Уэсли, 1992, p. 459.