Документация

TF = islocalmin(A) возвращает логический массив, элементы которого равняются 1 (true) когда локальный минимум обнаруживается в соответствующем элементе массива, таблицы или расписания.

TF = islocalmin(A,dim) задает размерность A действовать вперед. Например, islocalmin(A,2) находит локальные минимумы каждой строки матричного A.

TF = islocalmin(___,Name,Value) задает дополнительные параметры для нахождения локальных минимумов с помощью одного или нескольких аргументов пары "имя-значение". Например, islocalmin(A,'SamplePoints',t) находит локальные минимумы A относительно меток времени, содержавшихся во временном векторе t.

[TF,P] = islocalmin(___) также возвращает выдающееся положение, соответствующее каждому элементу A для любого из предыдущих синтаксисов.

Примеры

Локальные минимумы в векторе

Вычислите и постройте локальные минимумы вектора данных.

x = 1:100;
A = (1-cos(2*pi*0.01*x)).*sin(2*pi*0.15*x);
TF = islocalmin(A);
plot(x,A,x(TF),A(TF),'r*')

Минимумы в матричных строках

Создайте матрицу данных и вычислите локальные минимумы для каждой строки.

A = -25*diag(ones(5,1)) + rand(5,5);
TF = islocalmin(A,2)

TF = 5x5 logical array

   0   0   0   1   0
   0   1   0   0   0
   0   0   1   0   0
   0   0   0   1   0
   0   0   1   0   0

Разделенные минимумы

Вычислите локальные минимумы вектора данных относительно меток времени в векторном t. Используйте 'MinSeparation' параметр, чтобы вычислить минимумы, которые на расстоянии по крайней мере в 45 минут.

t = hours(linspace(0,3,15));
A = [2 4 6 4 3 7 5 6 5 10 4 -1 -3 -2 0];
TF = islocalmin(A,'MinSeparation',minutes(45),'SamplePoints',t);
plot(t,A,t(TF),A(TF),'r*')

Плоские области минимумов

Задайте метод для указания на последовательные значения минимумов.

Вычислите локальные минимумы данных, которые содержат последовательные значения минимумов. Укажите на минимум каждой плоской области на основе первого вхождения того значения.

x = 0:0.1:5;
A = max(-0.75, sin(pi*x));
TF1 = islocalmin(A, 'FlatSelection', 'first');
plot(x,A,x(TF1),A(TF1),'r*')

Укажите на минимум каждой плоской области со всеми случаями того значения.

TF2 = islocalmin(A, 'FlatSelection', 'all');
plot(x,A,x(TF2),A(TF2),'r*')

Видные минимумы

Вычислите локальные минимумы вектора данных и их выдающегося положения, и затем постройте их с данными.

x = 1:100;
A = peaks(100);
A = A(50,:);
[TF1,P] = islocalmin(A);
P(TF1)

ans = 1×2

    2.7585    1.7703

plot(x,A,x(TF1),A(TF1),'r*')
axis tight

Вычислите самый видный минимум в данных путем определения минимального требования выдающегося положения.

TF2 = islocalmin(A,'MinProminence',2);
plot(x,A,x(TF2),A(TF2),'r*')
axis tight

Входные параметры

`A` — Входные данные
вектор | матрица | многомерный массив | таблица | расписание

Входные данные в виде вектора, матрицы, многомерного массива, таблицы или расписания.

`dim` — Операционная размерность
положительный целочисленный скаляр

Операционная размерность в виде положительного целочисленного скаляра. По умолчанию, islocalmin действует по первому измерению, размер которого не равняется 1.

Например, если A матрица, затем islocalmin(A,1) действует вдоль строк A, вычисление локальных минимумов для каждого столбца.

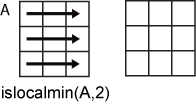
islocalmin(A,2) действует вдоль столбцов A, вычисление локальных минимумов для каждой строки.

Аргументы в виде пар имя-значение

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: TF = islocalmin(A,'MinProminence',2)

`'MinProminence'` — Минимальное выдающееся положение
0 (значений по умолчанию) | неотрицательный скаляр

Минимальное выдающееся положение в виде разделенной запятой пары, состоящей из 'MinProminence' и неотрицательный скаляр. islocalmin возвращает только локальные минимумы, выдающееся положение которых является, по крайней мере, заданным значением.

`'ProminenceWindow'` — Окно Prominence
положительный целочисленный скаляр | двухэлементный вектор положительных целых чисел | положительный скаляр длительности | двухэлементный вектор положительной длительности

Окно Prominence в виде разделенной запятой пары, состоящей из 'ProminenceWindow' и положительный целочисленный скаляр, двухэлементный вектор положительных целых чисел, положительного скаляра длительности или двухэлементного вектора положительной длительности. Значение задает окно соседних точек, для которых можно вычислить выдающееся положение для каждого локального минимума.

Когда значение окна является положительным целочисленным скаляром k, затем окно сосредоточено о каждом локальном минимуме и содержит элементы граничения k-1. Если k является четным, то окно сосредоточено о текущих и предыдущих элементах. Если локальный минимум в плоской области, то islocalmin обрабатывает целую плоскую область как центральную точку окна.

Когда значением является двухэлементный векторный [b f] из положительных целых чисел затем окно содержит локальный минимум, b элементы назад и f элементы вперед. Если локальный минимум в плоской области, то окно запускает b элементы перед первой точкой области и концов f элементы после последней точки области.

Когда входные данные являются расписанием или когда 'SamplePoints' задан как datetime или duration вектор, значение окна должно иметь тип duration, и окно вычисляется относительно точек выборки.

`'FlatSelection'` — Плоский индикатор области
`'center'` (значение по умолчанию) | `'first'` | `'last'` | `'all'`

Плоский индикатор области для того, когда локальное минимальное значение повторяется последовательно в виде разделенной запятой пары, состоящей из 'FlatSelection' и одно из следующего:

'center' — Укажите только на центральный элемент плоской области как локальный минимум. Элемент TF соответствие центру плоского равняется 1 и 0 для остающихся плоских элементов.
'first' — Укажите только на первый элемент плоской области как локальный минимум. Элемент TF соответствие запуску плоского равняется 1 и 0 для остающихся плоских элементов.
'last' — Укажите только на последний элемент плоской области как локальный минимум. Элемент TF соответствующий в конец плоского 1 и 0 для остающихся плоских элементов.
'all' — Укажите на все элементы плоской области как локальные минимумы. Элементы TF соответствие всем частям плоского равняется 1.

При использовании 'MinSeparation' или 'MaxNumExtrema' пары "имя-значение", плоские точки области совместно рассматриваются один минимальный вопрос.

`'MinSeparation'` — Минимальное разделение
0 (значений по умолчанию) | неотрицательный скаляр

Минимальное разделение между локальными минимумами в виде разделенной запятой пары, состоящей из 'MinSeparation' и неотрицательный скаляр. Разделительное значение задано в тех же модулях как вектор точек выборки, который является [1 2 3 ...] по умолчанию. Когда разделительное значение больше 0, islocalmin выбирает наименьший локальный минимум и игнорирует все другие локальные минимумы в рамках заданного разделения. Этот процесс повторяется, пока больше нет локальных обнаруженных минимумов.

Когда вектор точек выборки имеет, вводят datetime, разделительное значение должно иметь, вводят duration.

`'MaxNumExtrema'` — Максимальное количество минимумов
положительный целочисленный скаляр

Максимальное количество минимумов, обнаруженных в виде разделенной запятой пары, состоящей из 'MaxNumExtrema' и положительный целочисленный скаляр. islocalmin находит не больше, чем конкретное количество большинства видных минимумов, которое является длиной операционной размерности по умолчанию.

`'SamplePoints'` 'SamplePoints'
вектор

Точки выборки в виде разделенной запятой пары, состоящей из 'SamplePoints' и вектор. Точки выборки представляют местоположение данных в A. Точки выборки не должны быть однородно произведены, но должны быть отсортированы с уникальными элементами. По умолчанию вектором точек выборки является [1 2 3 ...].

islocalmin не поддерживает эту пару "имя-значение", когда входные данные являются расписанием.

`'DataVariables'` — Табличные переменные
имя переменной | массив ячеек имен переменных | числовой вектор | логический вектор | указатель на функцию | таблица `vartype` индекс

Табличные переменные в виде разделенной запятой пары, состоящей из 'DataVariables' и имя переменной, массив ячеек имен переменных, числового вектора, логического вектора, указателя на функцию или таблицы vartype индекс. 'DataVariables' значение указывает который переменные входной таблицы или расписания, чтобы работать с. Это значение может быть одним из следующего:

Вектор символов, задающий одно имя табличной переменной
Массив ячеек из символьных векторов, где каждым элементом является имя табличной переменной
Вектор индексов табличной переменной
Логический вектор, элементы которого каждый соответствует табличной переменной, где true включает соответствующую переменную и false исключает его
Указатель на функцию, который берет табличную переменную в качестве входа и возвращает логический скаляр
Таблица vartype индекс

Заданные табличные переменные должны иметь числовой или logical ввод.

Пример: 'Age'

Пример: {'Height','Weight'}

Пример: @isnumeric

Пример: vartype('numeric')

Выходные аргументы

`TF` — Локальный индикатор минимумов
вектор | матрица | многомерный массив

Локальный индикатор минимумов, возвращенный как вектор, матрица или многомерный массив. TF одного размера с A.

Типы данных: логический

`P` — Выдающееся положение
вектор | матрица | многомерный массив

Выдающееся положение, возвращенное как вектор, матрица или многомерный массив. P одного размера с A.

Если входные данные имеют целое число со знаком или тип беззнаковых целых чисел, то P беззнаковое целое.

Больше о