Функции построения графиков

Постройте график оптимизации во время выполнения

Можно построить различные показатели прогресса во время выполнения решателя. Установите PlotFcn пара "имя-значение" в optimoptions, и задайте одну или несколько функций построения графика для решателя, чтобы вызвать на каждой итерации. Передайте указатель на функцию или cell-массив указателей на функцию.

Существует множество предопределенных доступных функций построения графика. См.:

PlotFcn описание опции на странице ссылки на функцию решателя
Optimization app > Options > Plot functions

Можно также использовать пользовательски записанную функцию построения графика. Запишите файл функции с помощью той же структуры в качестве выходной функции. Для получения дополнительной информации об этой структуре смотрите Синтаксис Выходной функции.

Использование функции построения графика

В этом примере показано, как использовать функцию построения графика, чтобы просмотреть прогресс fmincon алгоритм внутренней точки. Проблема взята из Начала работы, Решают Ограниченную Нелинейную задачу, Основанную на решателе. Первая часть примера показывает, как запустить оптимизацию с помощью приложения Оптимизации. Вторая часть показывает, как запустить оптимизацию из командной строки.

Примечание

Приложение Оптимизации предупреждает, что будет удалено в будущем релизе.

Выполнение оптимизации Используя приложение оптимизации

Запишите нелинейную цель и ограничительные функции, включая производные:

function [f g H] = rosenboth(x)
% ROSENBOTH returns both the value y of Rosenbrock's function
% and also the value g of its gradient and H the Hessian.

f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

if nargout > 1
    g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
        200*(x(2)-x(1)^2)];
    
    if nargout > 2
        H = [1200*x(1)^2-400*x(2)+2, -400*x(1);
            -400*x(1), 200];  
    end
end

Сохраните этот файл как rosenboth.m.

function [c,ceq,gc,gceq] = unitdisk2(x)
% UNITDISK2 returns the value of the constraint
% function for the disk of radius 1 centered at
% [0 0]. It also returns the gradient.

c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];

if nargout > 2
    gc = [2*x(1);2*x(2)];
    gceq = [];
end

Сохраните этот файл как unitdisk2.m.

Запустите приложение Оптимизации путем ввода optimtool в командной строке.
Настройте оптимизацию:
- Выберите fmincon решатель.
- Выберите Interior point алгоритм.
- Установите целевую функцию на @rosenboth.
- Выберите Gradient supplied для производной целевой функции.
- Установите стартовую точку на [0 0].
- Установите нелинейную ограничительную функцию на @unitdisk2.
- Выберите Gradient supplied для нелинейных ограничительных производных.
Ваша панель Problem Setup and Results должна соответствовать следующему рисунку.
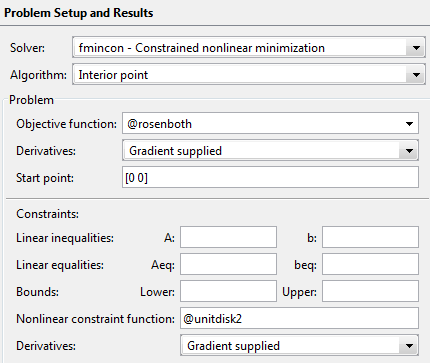
Выберите три функции построения графика в панели Options: Current point, Function value и First order optimality.
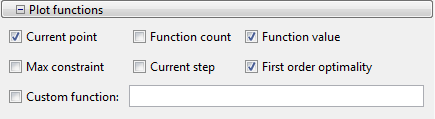
Нажмите кнопку Start под Run solver and view results.
Вывод появляется следующим образом в приложении Оптимизации.
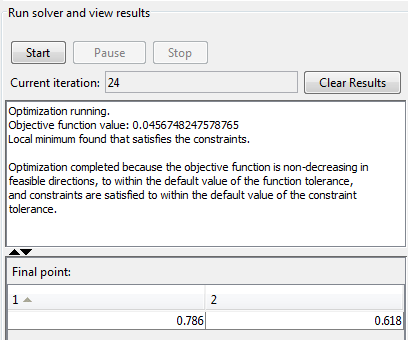
Кроме того, следующие три графика появляются в отдельном окне.

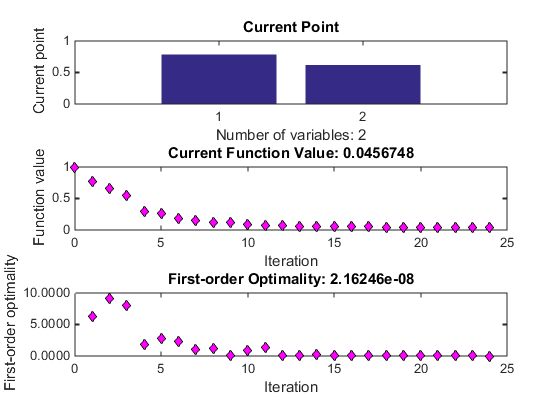
График “Current point” графически показывает минимизатору [0.786,0.618], о котором сообщают как Final point в панели Run solver and view results. Этот график обновления в каждой итерации, показывая промежуточное звено выполняет итерации.
“Текущее Значение функции” график показывает значение целевой функции во всех итерациях. Этот график является почти монотонным, показывая fmincon уменьшает целевую функцию почти при каждой итерации.
График “Оптимальность Первого порядка” показывает меру оптимальности первого порядка во всех итерациях.

Выполнение оптимизации из командной строки

Запишите нелинейную цель и ограничительные функции, включая производные, как показано в Выполнении Оптимизации Используя Приложение Оптимизации.

Создайте структуру опций, которая включает вызов этих трех функций построения графика:

options = optimoptions(@fmincon,'Algorithm','interior-point',...
 'SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true,'PlotFcn',{@optimplotx,...
    @optimplotfval,@optimplotfirstorderopt});

Вызовите fmincon:

x = fmincon(@rosenboth,[0 0],[],[],[],[],[],[],...
    @unitdisk2,options)

fmincon дает следующий выход:

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is
non-decreasing in feasible directions, to within the default
value of the function tolerance, and constraints are satisfied
to within the default value of the constraint tolerance.

x =
    0.7864    0.6177

fmincon также отображает эти три функции построения графика, показанные в конце Выполнения Оптимизации Используя Приложение Оптимизации.

Документация