Количество итераций в оптимизации зависит от stopping criteria решателя. Эти критерии включают несколько tolerances, который можно установить. Обычно допуск является порогом, который, если пересечено, останавливает итерации решателя.
Установите погрешности и другие критерии с помощью optimoptions как объяснено в Опциях Набора и Изменения.
Обычно устанавливайте погрешности, такие как OptimalityTolerance и StepTolerance быть много больше eps, и обычно выше 1e-14. Устанавливание маленьких погрешностей не всегда приводит к точным результатам. Вместо этого решатель может не распознать, когда он сходился и может продолжить бесполезные итерации. Значение допуска, меньшее, чем eps эффективно отключает то условие остановки. Этот совет не применяется к fzero, который использует значение по умолчанию eps для TolX допуск.
Можно найти допуски по умолчанию в Приложении Оптимизации. Некоторые допуски по умолчанию отличаются для различных алгоритмов, таким образом установите и решатель и алгоритм.

optimoptions допуски отображений. Например,
options = optimoptions('fmincon');
[options.OptimalityTolerance,options.FunctionTolerance,options.StepTolerance]ans =
1.0e-06 *
1.0000 1.0000 0.0001Можно также найти допуски по умолчанию в разделе опций страницы ссылки на функцию решателя.
StepTolerance нижняя граница на размер шага, означая норму (xi – x i +1). Если решатель пытается получить шаг, который меньше, чем StepTolerance, завершение итераций. StepTolerance обычно используется в качестве относительной границы, означая завершение итераций когда | (xi – x i +1) | <StepTolerance* (1 + |xi |), или подобная относительная мера. Смотрите Детали Допуска.
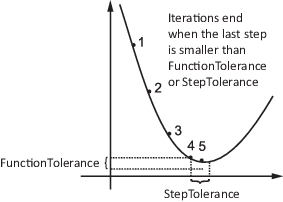
Для некоторых алгоритмов, FunctionTolerance нижняя граница на изменении в значении целевой функции во время шага. Для тех алгоритмов, если |f (xi) – f (x i +1) | <FunctionTolerance, завершение итераций. FunctionTolerance обычно используется в качестве относительной границы, означая завершение итераций когда |f (xi) – f (x i +1) | < FunctionTolerance* (1 + |f (xi) |), или подобная относительная мера. Смотрите Детали Допуска.
В отличие от других решателей, fminsearch остановки, когда это удовлетворяет обоим
TolFun (функциональный допуск) и TolX (допуск шага).
OptimalityTolerance погрешность меры оптимальности первого порядка. Если мера оптимальности меньше OptimalityTolerance, завершение итераций. OptimalityTolerance может также быть относительная граница в мере оптимальности первого порядка. Смотрите Детали Допуска. Мера оптимальности первого порядка задана в Мере оптимальности Первого порядка.
ConstraintTolerance верхняя граница на величине любых ограничительных функций. Если решатель возвращает точку x с c (x) > ConstraintTolerance или |ceq (x) | > ConstraintTolerance, решатель сообщает, что ограничения нарушены в x. ConstraintTolerance может также быть относительная граница. Смотрите Детали Допуска.
ConstraintTolerance действует по-другому по сравнению с другими допусками. Если ConstraintTolerance не удовлетворен (т.е. если величина ограничительной функции превышает ConstraintTolerance), решатель пытается продолжиться, если он не остановлен по другой причине. Решатель не останавливается просто потому что ConstraintTolerance удовлетворен.
MaxIterations граница на количество итераций решателя. MaxFunctionEvaluations граница на количество функциональных оценок. Итерации и вычисления функции обсуждены в Итерациях и Функциональных количествах.
Существует два других допуска, которые применяются к конкретным решателям: TolPCG и MaxPCGIter. Они относятся к предобусловленным шагам метода сопряженных градиентов. Для получения дополнительной информации смотрите Предобусловленный Метод сопряженных градиентов.
Существует несколько допусков, которые применяются только к fmincon алгоритм внутренней точки. Для получения дополнительной информации см. Алгоритм Внутренней точки в fmincon options.
Существует несколько допусков, которые применяются только к intlinprog. Смотрите, что некоторые “целочисленные” решения не являются Целыми числами и ветвью и связанный.