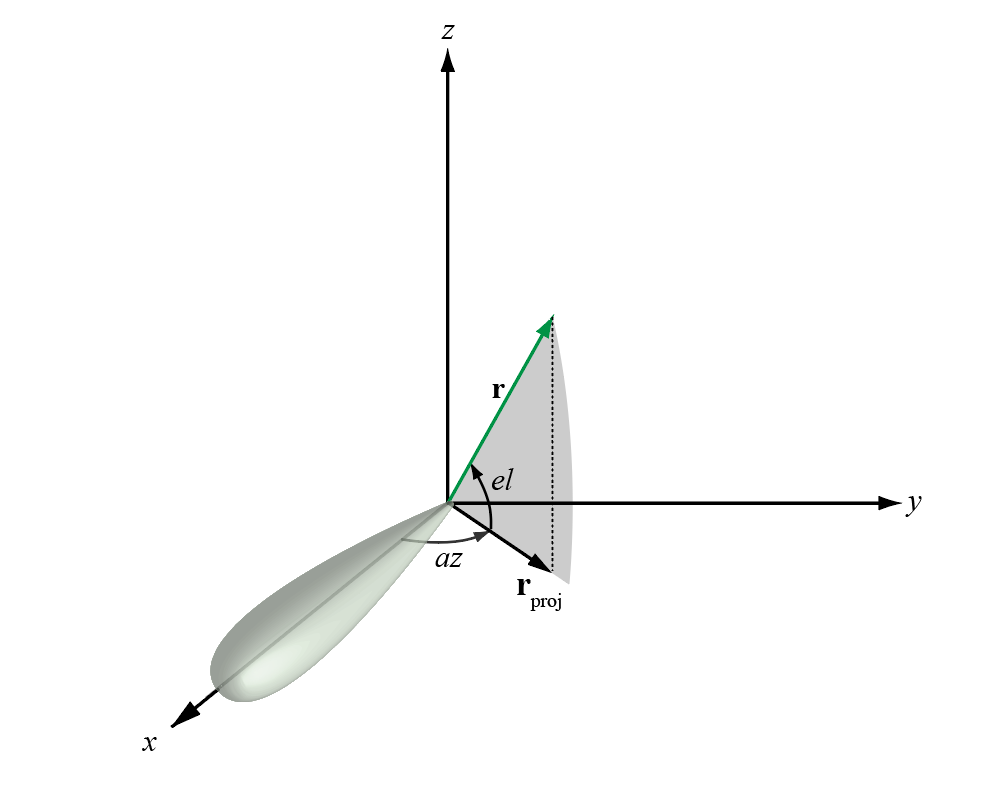
azimuth angle вектора является углом между x - ось и ортогональной проекцией вектора на плоскость xy. Угол положителен в движении от оси x к оси y. Углы азимута находятся между –180 и 180 градусами. elevation angle является углом между вектором и его ортогональной проекцией на xy - плоскость. Угол положителен при движении к положительному z - ось от плоскости xy. По умолчанию направление опорного направления элемента или массива выравнивается с положительным x - ось. Направление опорного направления является направлением основного лепестка элемента или массива.

Этот рисунок иллюстрирует угол азимута и угол вертикального изменения для вектора, показавшего зеленой сплошной линией.

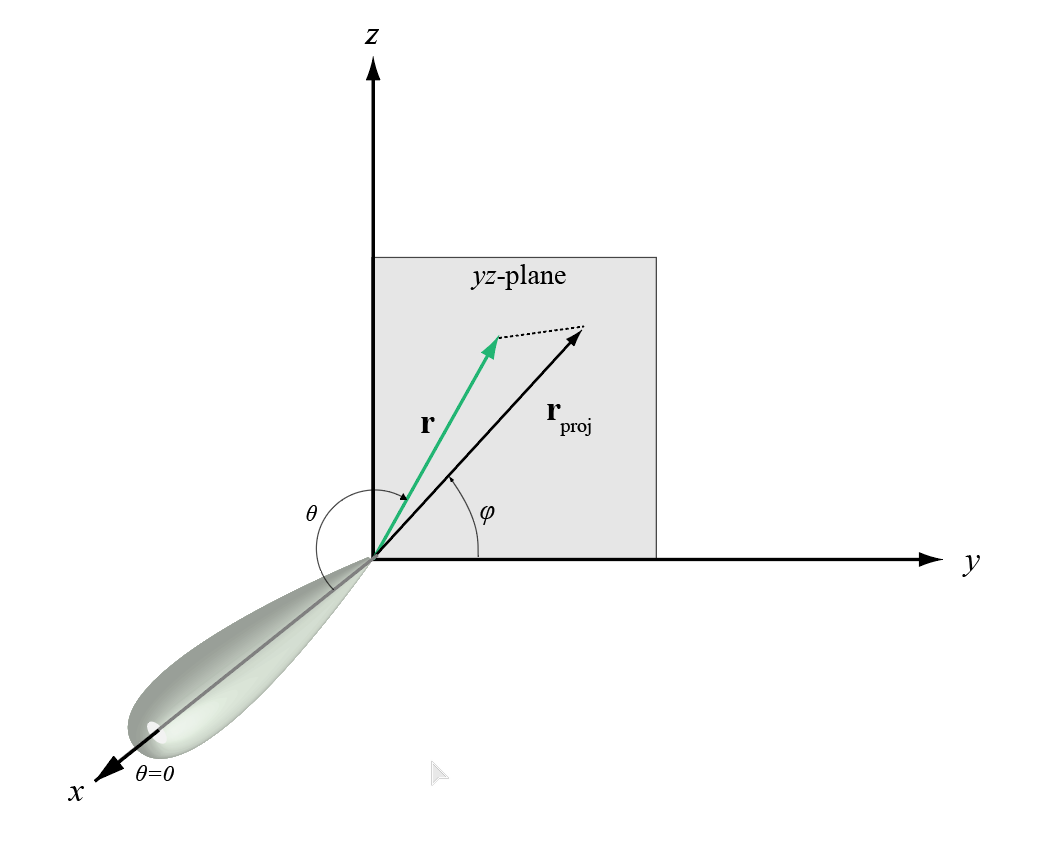
phi угол (φ) является углом от положительного y - ось к ортогональной проекции вектора на плоскость yz. Угол положителен к положительному z - ось. phi угол между 0 и 360 градусами. Угол теты (θ) является углом от x - ось к самому вектору. Угол положителен к плоскости yz. Угол теты между 0 и 180 градусами.

Фигура иллюстрирует phi и тету для вектора, который появляется как зеленая сплошная линия.

Координатные преобразования между φ/θ и az/el описаны следующими уравнениями

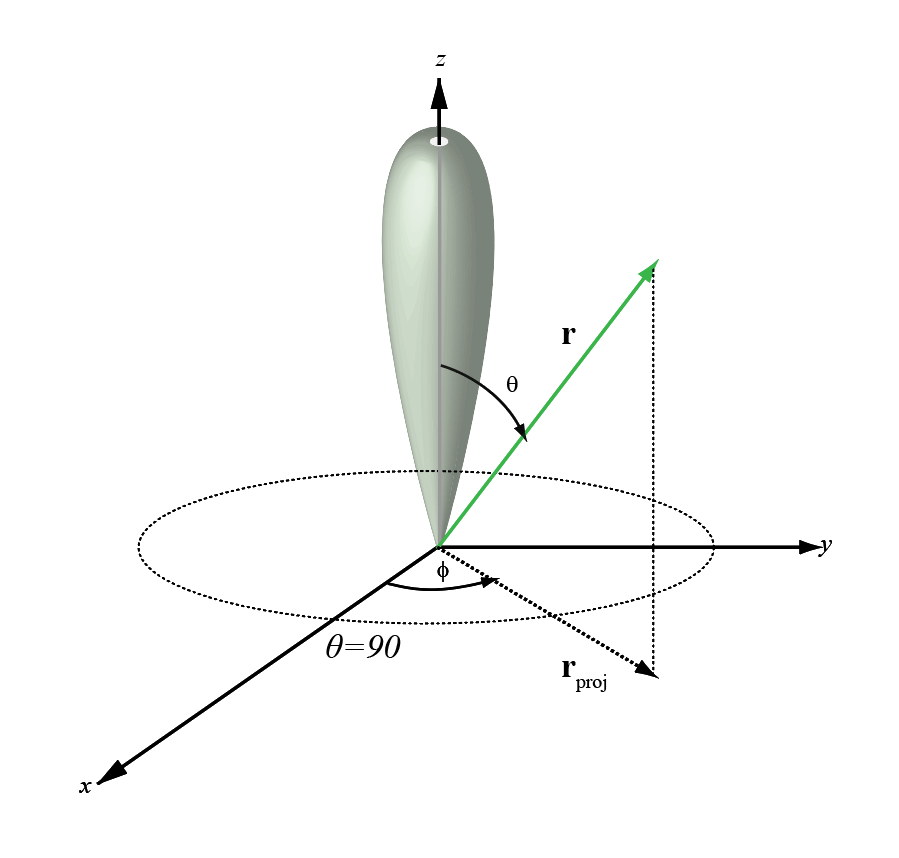
phi угол (φ) является углом от положительного x - ось к ортогональной проекции вектора на плоскость xy. Угол положителен к положительному y - ось. phi угол между 0 и 360 градусами. Угол теты (θ) является углом от z - ось к самому вектору. Угол положителен к плоскости xy. Угол теты между 0 и 180 градусами.

Фигура иллюстрирует φ и θ для вектора, который появляется как зеленая сплошная линия.

Это преобразование применяется когда RotAx false.