Уменьшайте числовую жесткость

Этот пример помогает вам завершить шаги, обрисованные в общих чертах в режиме реального времени Рабочий процесс Подготовки Модели и удовлетворить целям, описанным в Целях Подготовки Модели.

В Определяют Размер Шага, вы используете результаты симуляции переменного шага вашей модели Simscape™, чтобы идентифицировать, когда размер шага уменьшается, чтобы получить поведение точно в разрывах и для быстрой динамики в численно жестких системах. Эти типы событий часто требуют, чтобы решатели предприняли шаги, которые слишком малы, чтобы поддержать симуляцию в реальном времени. В этом примере показано, как использовать результаты, Определяют Размер Шага, чтобы идентифицировать численно жесткий элемент в вашей модели. Это также показывает, как изменить элемент для более быстрой симуляции, не жертвуя точностью.

Почему уменьшают жесткость?

Числовая жесткость может препятствовать тому, чтобы ваша модель была в реальном времени способный. Способная к реальному времени модель является той, которая приводит к приемлемым результатам, не подвергаясь переполнениям, когда вы симулируете его на своем целевом процессоре. Жесткие системы содержат движущие силы, которые варьируются и быстро и медленно. Когда решатели делают большие шаги, они обычно получают медленно изменяющуюся динамику, но они имеют тенденцию пропускать быстрые изменения, если они не делают небольшие шаги. Размеры небольшого шага вызывают переполнения, когда они не обеспечивают достаточно времени для компьютера в реальном времени, чтобы завершить вычисление решений во время одного шага.

Вам уменьшают числовую жесткость, вы устраняете быстрые изменения. Если нет никаких быстрых изменений, решатель может сделать большие шаги и все еще получить точные результаты симуляции. Чем больше размер шага, тем менее вероятно случается так, что ваша модель генерирует переполнение во время симуляции в реальном времени.

Рассмотрите ссылочные результаты

Открыть модель, в командной строке MATLAB^®, введите:
```
model = 'ssc_pneumatic_rts_reference';
open_system(model)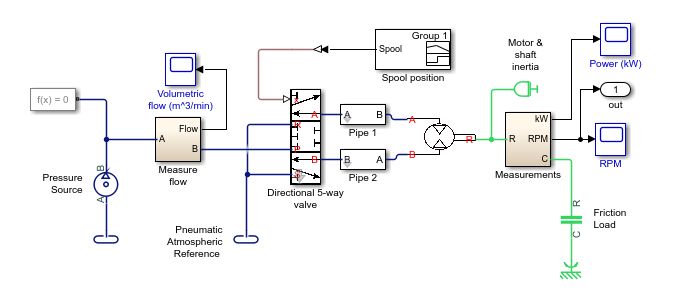
```
Симулируйте модель:
```
sim(model)
```
Создайте фигуру, которая содержит полулогарифмический график размера шага решателя, график результатов частоты вращения двигателя и график результатов потока газа.
```
h1 = figure;
subplot(3,1,1)
semilogy(tout(1:end-1),diff(tout),'-x')
title('Solver Step Size and Results')
ylabel('Step Size (s)')
subplot(3,1,2)
plot(tout,Pneu_rts_RPM_DATA.signals.values)
ylabel('Speed (rpms)')
subplot(3,1,3)
plot(tout,Pneu_rts_Vol_Flow_DATA.signals.values)
xlabel('Time (s)')
ylabel('Flow Rate (m^3/min)')
```
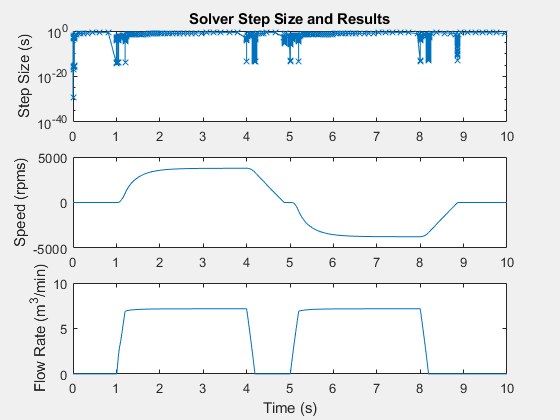
Симуляция предпринимает шаги меньшая, чем 1e-10 секунды когда:
- Частота вращения двигателя является близким нулевым об/мин (время симуляции t = ~ 1, 5, и 9 секунд)
- Ступенчатое изменение в частоте вращения двигателя инициируется от установившейся скорости до новой скорости (время t = ~ 4 и 8 секунд)
- Ступенчатое изменение в скорости потока жидкости инициируется от установившейся скорости до новой скорости потока жидкости (время t = ~ 4 и 8 секунд)
- Объемный расход является близким нулевым м^3/min (t = ~ 1, 4, и 5 секунд),
Результаты показывают, что размеры небольшого шага требуются, чтобы достигать точности, когда симуляция получает движущие силы, которые включают трение или маленькие, сжимаемые объемы. Элементы, которые генерируют нулевые пересечения, могут также быть ответственны за небольшие шаги и замедлить времена восстановления.
Присвойте результаты симуляции новым переменным в рабочем пространстве MATLAB так, чтобы можно было сравнить данные с результатами модели, которую вы изменяете.
```
timeRef  = tout;
simlogRef = simlog;
```

Идентифицируйте и измените жесткий элемент

Исследуйте загрузку трения в модели, чтобы определить, включает ли это разрывы или имеет небольшую постоянную времени, которая вызывает числовую жесткость. Измените элемент, если он вызывает какие-либо быстро изменяющиеся движущие силы, которые требуют размера небольшого шага.

Сохраните модель как rts_stiffness_model в перезаписываемой папке на пути MATLAB.
Откройте диалоговое окно блока Загрузки Трения, блок Rotational Friction. Рисунок показывает момент трения / относительная скоростная характеристика для простого приближения непрерывного трения что модели блока.

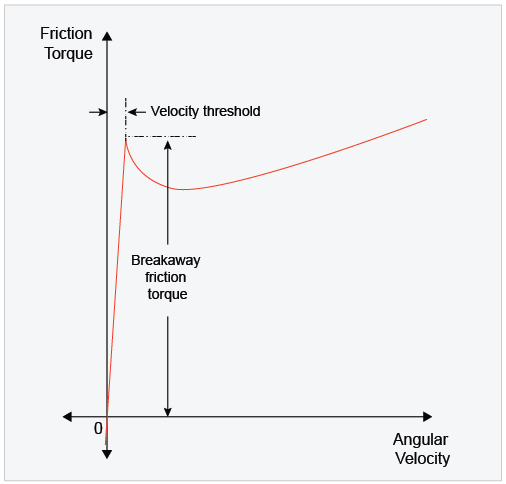
Момент срыва моделируется как функция скоростного порога. Когда скорость близко к нулю, небольшое изменение в скорости дает к большому изменению в крутящем моменте. Когда скорость не близко к нулю, изменение крутящего момента более постепенно. Этот блок представляет жесткий элемент. Чтобы сделать элемент менее жестким, задайте более высокое значение для Breakaway friction velocity.
На вкладке Parameters диалогового окна измените Breakaway friction velocity от 0.059137 к 0.1 rad/s.
Симулируйте модифицированную модель.

Анализ результатов

Чтобы видеть, как изменение скоростного порога для блока трения влияет на жесткость компонента, сравните размеры шага для этих двух симуляций. Ссылочные результаты оправдывают надежды на основе эмпирических и теоретических данных. Можно оценить точность модифицированной модели путем сравнения скорости, следует из модифицированной модели к результатам исходной версии модели.

Постройте размер шага для ссылочных результатов для модифицированной модели фигуре, которая содержит справочные данные.
```
h2 = figure;
semilogy(timeRef(1:end-1),diff(timeRef),'-x',...
	'LineWidth',1,'MarkerSize',7)
hold on
semilogy(tout(1:end-1),diff(tout),'--x','Color','r',...
	'LineWidth',.1,'MarkerSize',5)
title('Solver Step Size')
xlabel('Time (s)')
ylabel('Step Size (s)')
h1Leg = legend({'Reference','Modified'},'Location','best');
```
Размер шага восстанавливается более быстро с события, которое происходит во времени симуляции t = 4 и 9 секунд. Симуляция менее жестка в эти времена.

Извлеките скорость и данные времени из узлов логгирования для исходных и модифицированных моделей.

speedRefNode = simlogRef.Measurements.Ideal_Rotational_Motion_Sensor.R.w;
speedRef = speedRefNode.series.values('rpm');
timeRef = speedRefNode.series.time;
speedModNode = simlog.Measurements.Ideal_Rotational_Motion_Sensor.R.w;
speedMod = speedModNode.series.values('rpm');
timeMod = speedModNode.series.time;

Постройте и сравните результаты для данных о скорости для обеих симуляций, чтобы убедиться, что модифицированная модель точна.
```
h3 = figure;
plot(timeRef,speedRef)
h3;
hold on
plot(timeMod,speedMod,'r--')
title('Speed')	
xlabel('Time (s)')
ylabel('Speed (rpms)')
h3Leg = legend({'Reference','Modified'},'Location','best');
```
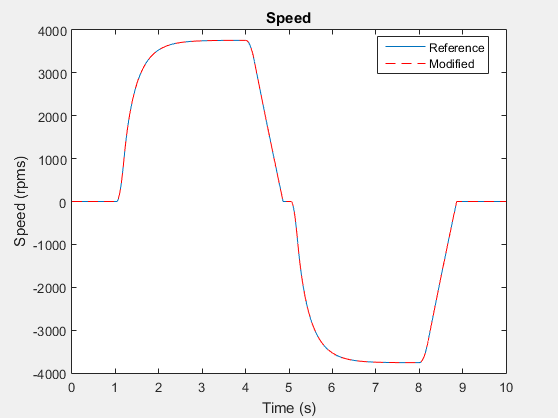
Масштабируйте для более внимательного рассмотрения в точке перегиба во время (t) = ~5 секунд.
```
h3;
xStart = 0;
xEnd = 10;
yStart = -4000;
yEnd = 4000;
xZoomStart1 = 4.8;
xZoomEnd1 = 5.2;
yZoomStart1 = -400;
yZoomEnd1 = 150;
axis([xZoomStart1 xZoomEnd1 yZoomStart1 yZoomEnd1])
```
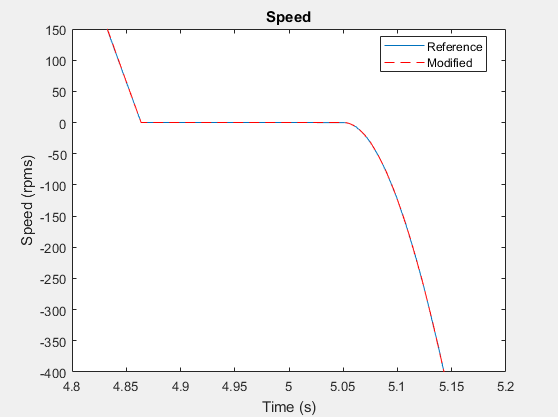
На этом уровне изменения масштаба вы видите, что результаты симуляции для модифицированной модели достаточно точны, чтобы оправдать надежды на основе эмпирических и теоретических данных.

Загрузка Трения теперь менее численно жестка. Рисунок размера шага в процессе моделирования показывает, что другие элементы в модели также ответственны в течение медленных времен восстановления. Уменьшайте больше шагов медленного восстановления путем исследования и изменения других элементов та жесткость причины.

Можно также увеличиться, скорость путем изменения методов использования модели в Уменьшают Затраты на Расчет и Уменьшают Нулевые Пересечения. Если можно устранить все небольшие шаги, которые могут сгенерировать переполнение, можно попытаться запуститься, симуляция фиксированного шага с помощью методов в Выбирают Step Size и Number of Iterations.

Документация