Программное обеспечение RF Blockset™ Equivalent Baseband симулирует физическую систему в области времени использование комплексной основополосно-эквивалентной модели, которую это создает из параметров частотного диапазона полосы пропускания физических блоков. Этот тип моделирования также известен как lowpass, эквивалентный (LPE), комплексный конверт или моделирование конверта.
Чтобы создать комплексную основополосно-эквивалентную модель во временном интервале на основе сетевых параметров физической системы, blockset выполняет математическое преобразование, которое состоит из выполняющего трех шагов:
blockset вычисляет передаточную функцию полосы пропускания от физических параметров блоков на частотах моделирования путем вычисления передаточной функции физической подсистемы и затем применения окна Tukey, чтобы получить передаточную функцию полосы пропускания.
Чтобы изучить, как blockset использует заданные сетевые параметры, чтобы вычислить сетевые параметры на частотах моделирования, смотрите Параметры Сети Карты к Моделированию Частот.
Передаточная функция физической подсистемы задана как:
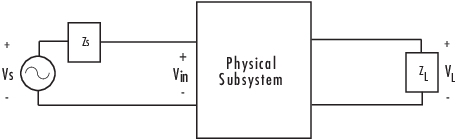
где VS и VL являются источником и загружают напряжения, показанные в следующем рисунке, и f представляет частоты моделирования.
А именно,
где
и
ZS является исходным импедансом.
ZL является импедансом загрузки.
Sij являются S-параметры сети 2D порта.
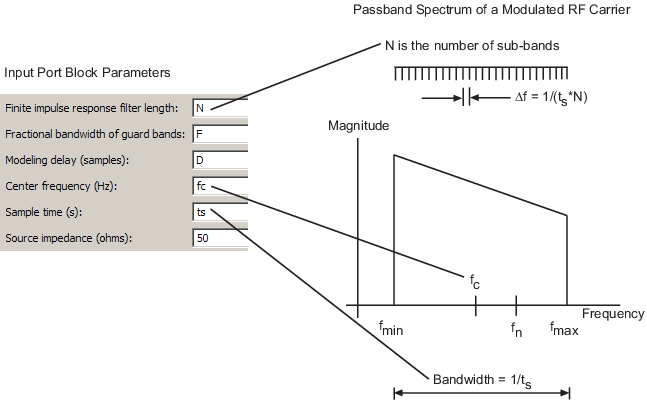
blockset выводит передаточную функцию физической подсистемы от параметров блоков Input port как показано в следующем рисунке.
blockset затем применяет окно Tukey, чтобы получить передаточную функцию полосы пропускания:
где tukeywin tukeywin Signal Processing Toolbox™ функция.
blockset вычисляет основополосную передаточную функцию, , путем перевода передаточной функции полосы пропускания в ее эквивалентную основополосную передаточную функцию:
где ФК является заданной центральной частотой.
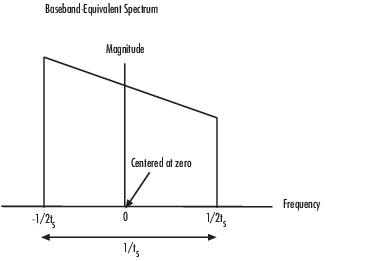
Получившийся основополосно-эквивалентный спектр сосредоточен в нуле, таким образом, blockset может симулировать систему с помощью намного большего временного шага, чем Simulink® может использовать в той же системе. Для получения информации о том, почему этот перевод допускает больший временной шаг, смотрите КПД Симуляции Основополосно-эквивалентной Модели.
Основополосную передаточную функцию показывают в следующем рисунке.
blockset вычисляет основополосно-эквивалентную импульсную характеристику путем выполнения следующих шагов:
Вычислите обратный БПФ основополосной передаточной функции. Для более быстрой симуляции блок вычисляет ОБПФ с помощью следующей степени 2 больших, чем заданная конечная длина фильтра импульсной характеристики. Затем это обрезает импульсную характеристику до длины, равной заданной длине фильтра. Когда конечная импульсная характеристика является усеченной к длине, заданной пользователем, эффект усечения похож на работу с окнами с прямоугольным окном.
Примените задержку, заданную параметром Modeling delay (samples) в диалоговом окне блока Input port. Выбор соответствующего значения для этой задержки гарантирует, что основополосно-эквивалентная модель имеет причинный ответ путем перемещения окна времени, таким образом, что энергия модели сконцентрирована в центре окна как показано в следующем рисунке:
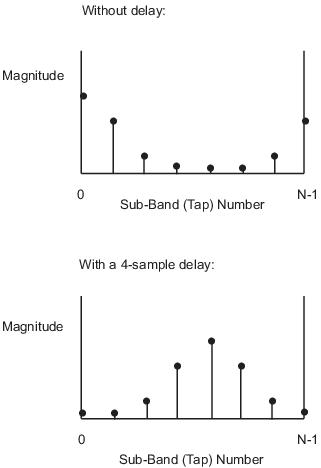
Основополосно-эквивалентная техника моделирования улучшает скорость симуляции, позволяя средству моделирования взять большие временные шаги. Чтобы симулировать систему во временном интервале, Simulink потребовал бы размера шага:
Используя основополосно-эквивалентную модель той же системы, спектр которой был смещен вниз ФК, допускает намного больший временной шаг:
Основополосно-эквивалентный обзор моделирования в качестве примера
Сокращение некаузального ответа в основополосно-эквивалентной модели
В этом примере вы моделируете линию электропередачи РФ, стимулированную импульсом, и строите основополосно-эквивалентную модель что использование blockset, чтобы симулировать линию электропередачи во временном интервале. Вы сравниваете эффекты использования различных значений параметров для основополосно-эквивалентной модели. Этот пример помогает вам изучить, как использовать эти параметры, чтобы лучше всего применить основополосно-эквивалентную парадигму моделирования выполнения симуляции временного интервала с помощью ограниченной полосы данных о частоте.
В этой части примера вы выполняете следующие задачи:
Выберите Blocks to Represent System Components. В этой части примера вы выбираете блоки, чтобы представлять:
Входной сигнал
Линия электропередачи РФ
Основополосно-эквивалентное отображение модели
В следующей таблице перечислены блоки, которые представляют компоненты системы и описание роли каждого блока.
Блок | Описание |
|---|---|
| Discrete Impulse | Генерирует основанный на системе координат импульсный входной сигнал. |
| Real-Imag to Complex | Преобразует действительный импульсный сигнал в комплексный импульсный сигнал. |
| Input Port | Устанавливает параметры, которые характерны для всех блоков в подсистеме линии электропередачи РФ, включая исходный импеданс подсистемы, которая используется, чтобы преобразовать Сигналы Simulink в физическую среду моделирования. |
| RLCG Transmission Line | Моделирует затухание сигнала, вызванное линией электропередачи РФ. |
| Output Port | Устанавливает параметры, которые характерны для всех блоков в подсистеме линии электропередачи РФ. Эти параметры включают импеданс загрузки подсистемы, которая используется, чтобы преобразовать сигналы РФ в Сигналы Simulink. |
| Complex to Magnitude-Angle | Преобразует комплексный сигнал от блока Output Port в формат угла величины. |
Создайте Модель. В этой части примера вы создаете модель Simulink, добавляете блоки в модель и соединяете блоки.
Создайте модель.
Добавьте в модель блоки, показанные в следующей таблице. Столбец Пути к библиотеке таблицы задает иерархический путь к каждому блоку.
Блок | Путь к библиотеке | Количество |
|---|---|---|
| Discrete Impulse | DSP System Toolbox> Sources | 1 |
| Real-Imag to Complex | Simulink> Math Operations | 1 |
| Input Port | RF Blockset> Equivalent Baseband> Input/Output Ports | 1 |
| RLCG Transmission Line | RF Blockset> Equivalent Baseband> Transmission Lines | 1 |
| Output Port | RF Blockset> Equivalent Baseband> Input/Output Ports | 1 |
| Complex to Magnitude-Angle | Simulink> Math Operations | 1 |
Соедините блоки как показано в следующем рисунке.
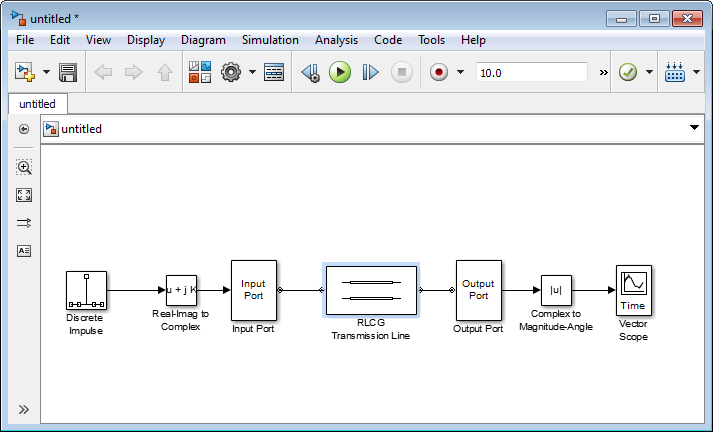
Теперь вы готовы задать переменные модели.
Задайте Переменные Модели. Введите следующее в подсказке MATLAB®, чтобы настроить переменные рабочей области для модели:
t_s = 5e-10; % Sample time f_c = 3e9; % Center frequency taps = 64; % Filter length
Теперь вы готовы задать параметры блоков.
В этой части примера вы задаете следующие параметры, чтобы представлять поведение компонентов системы:
Параметры Входного сигнала. Вы генерируете основанный на системе координат комплексный импульсный исходный сигнал использование двух блоков:
Блок Discrete Impulse генерирует действительный импульсный сигнал.
Блок Real-Imag to Complex преобразует действительный сигнал в комплексный сигнал.
Все сигналы в модели РФ должны быть комплексными, чтобы совпадать с сигналами в физической подсистеме, таким образом, вы создаете комплексный входной сигнал.
В Дискретном Импульсном диалоговом окне параметров блоков:
Установите Sample time на t_s.
Установите Samples per frame на 2*taps.
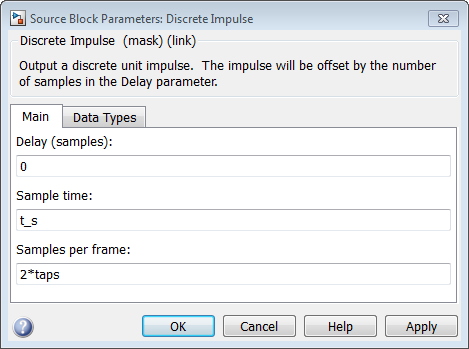
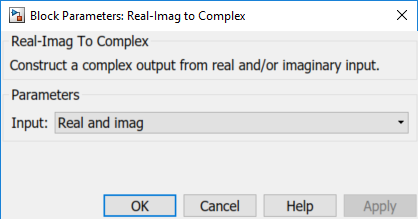
Установите Действительное-Imag на блок Complex параметр Input к Real. Изменение этого параметра изменяет количество входных параметров блока с два до одного, делая блок полностью соединенным.
Параметры Подсистемы Линии электропередачи. В этой части примера вы конфигурируете блоки, которые моделируют подсистему фильтра РФ — Input Port, Transmission Line и блоки Output Port.
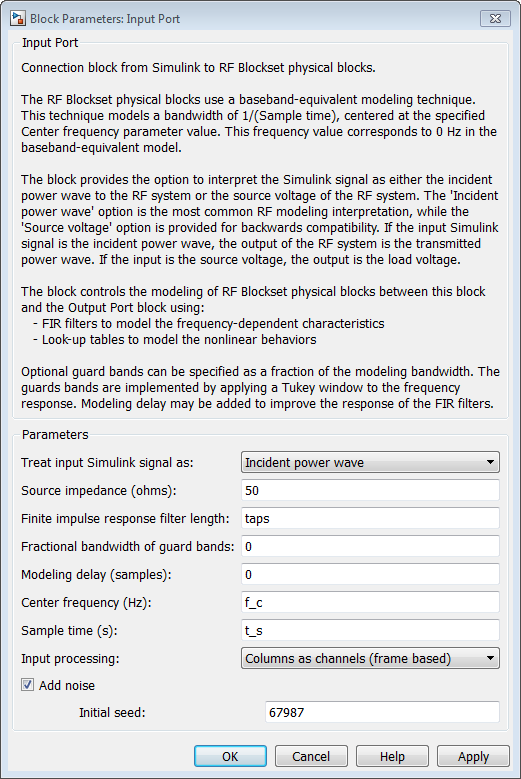
В диалоговом окне параметров блоков Input port:
Установите Treat input Simulink signal as на Incident power wave.
Эта опция говорит blockset интерпретировать входной сигнал как инцидентную волну степени к подсистеме РФ, а не исходное напряжение подсистемы РФ.
Если вы используете значение по умолчанию в этом параметре, программное обеспечение интерпретирует входной Сигнал Simulink как исходное напряжение. В результате источник и загрузка, которые моделируют Input port и блоки Выходного порта, соответственно, вводят 6 дБ потери в физическую систему на всех частотах. Для получения дополнительной информации о том, почему происходит эта потеря, см. примечание в Преобразовании в и от Сигналов Simulink.
Установите Finite impulse response filter length на taps.
Установите Center frequency на f_c.
Установите Sample time (s) на t_s.
Этот шаг расчета эквивалентен пропускной способности моделирования 1/t_s секунды.
Set Input Processing к Columns as channels (frame based).
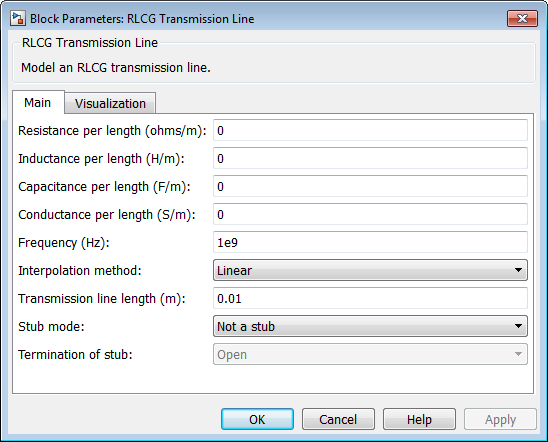
В диалоговом окне параметров блоков Линии электропередачи RLCG:
Установите Inductance per length (H/m) на 50.
Установите Capacitance per length (F/m) на .02.
Установите Frequency (Hz) на f_c.
Установите Transmission line length (m) на 0.5*t_s.
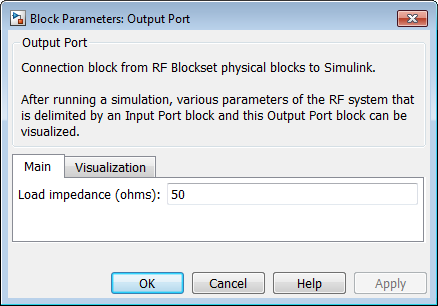
Примите, что параметры по умолчанию для блока Output Port используют импеданс загрузки 50 Ом.
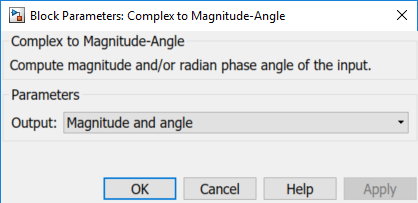
Параметры Отображения сигнала. В этой части примера вы задаете параметры, которые настраивают основополосно-эквивалентное отображение модели. Вы используете блок Complex to Magnitude-Angle, чтобы преобразовать подсистему РФ выход в формат величины.
Установите блок Complex to Magnitude-Angle параметр Output на Magnitude. Изменение этого параметра изменяет количество блока выходные параметры с два до одного, делая блок полностью соединенным.
Прежде чем вы запустите симуляцию, установите время остановки. Нажмите Simulation In the PREPARE, нажмите Model Settings in Configuration and Simulation. Введите 2*t_s*(taps-1) для параметра Stop time.
Чтобы запустить симуляцию, нажмите Run в окне модели.
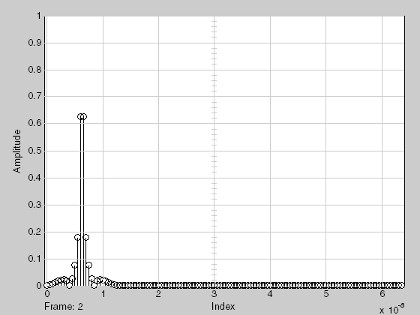
Это окно появляется автоматически, когда вы запускаете симуляцию. Следующий график показывает основополосно-эквивалентную модель, которая содержит существенное количество некаузальной энергии из-за ограниченной пропускной способности модели.
Основополосно-эквивалентная модель
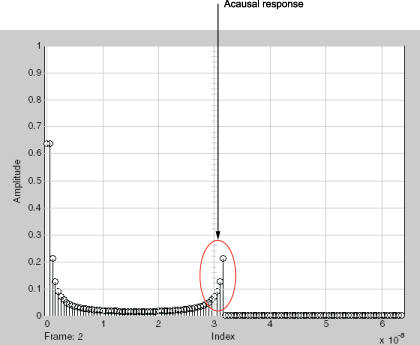
Следующая часть примера показывает вам, как уменьшать этот некаузальный ответ.
В этой части примера вы настраиваете параметр Fractional bandwidth of guard bands. Этот параметр управляет формированием фильтра, который blockset применяет, чтобы создать основополосно-эквивалентную модель.
Установите параметр Fractional bandwidth of guard bands Input port на 0.2.
Повторно выполните симуляцию.
Вы видите, что некаузальный ответ ниже, чем это было для предыдущей симуляции, но существует все еще некоторая энергия, переносящая конец модели, потому что это периодически.
Основополосно-эквивалентная модель с формированием фильтра
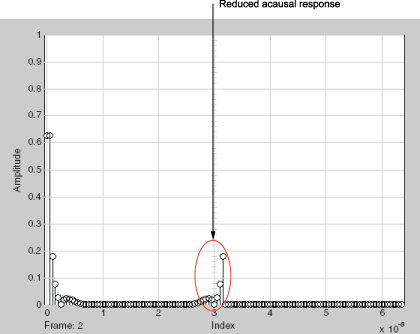
Можно далее уменьшать некаузальный ответ в основополосно-эквивалентной модели путем увеличения значения параметра Fractional bandwidth of guard bands выше 0.2, но если вы используете высокое значение, вы ставите под угрозу точность усиления линии электропередачи.
Следующий раздел показывает вам, как переключить ответ, чтобы избежать этого переноса.
В этой части примера вы настраиваете параметр Modeling delay (samples). Этот параметр управляет задержкой, которую blockset применяет, чтобы создать основополосно-эквивалентную модель.
Установите параметр Modeling delay (samples) Input port на 12.
Повторно выполните симуляцию.
Ответ основополосно-эквивалентной модели сконцентрирован в маленьком окне времени. Эта модель обеспечивает самую точную симуляцию временного интервала заданной полосы данных о частоте.
Основополосно-эквивалентная модель с формированием фильтра и задержкой