Постройте 3-D поверхность
fsurf( создает объемную поверхностную диаграмму символьного выражения f)f(x,y) на интервале по умолчанию [-5 5] для x и y.
fsurf( графики f,[xmin xmax
ymin ymax])f(x,y) на интервале [xmin xmax] для x и [ymin ymax] для y. fsurf функционируйте использует symvar заказать интервалы присвоения и переменные.
fsurf( строит параметрический поверхностный funx,funy,funz)x = x(u,v), y = y(u,v), z = z(u,v) на интервале [-5 5] для u и v.
fsurf( строит параметрический поверхностный funx,funy,funz,[uvmin
uvmax])x = x(u,v), y = y(u,v), z = z(u,v) на интервале [uvmin uvmax] для u и v.
fsurf( строит параметрический поверхностный funx,funy,funz,[umin
umax vmin vmax])x = x(u,v), y = y(u,v), z = z(u,v) на интервале [umin umax] для u и [vmin vmax] для v. fsurf функционируйте использует symvar заказать параметрические переменные и интервалы присвоения.
fsurf(___, использование LineSpec)LineSpec установить стиль линии, символ маркера и цвет поверхности. Используйте эту опцию после любой из предыдущих комбинаций входных аргументов.
fsurf(___, задает свойства линии с помощью одного или нескольких Name,Value)Name,Value парные аргументы. Используйте эту опцию после любой из комбинаций входных аргументов в предыдущих синтаксисах.
fsurf( графики в оси с объектом ax,___)ax вместо объекта gca текущей системы координат.
fs = fsurf(___)
Постройте вход в области значений по умолчанию и .
syms x y fsurf(sin(x)+cos(y))

Постройте действительную часть в области значений по умолчанию и .
syms f(x,y)
f(x,y) = real(atan(x + i*y));
fsurf(f)
График и путем определения интервала графического вывода в качестве второго аргумента fsurf.
syms x y f = sin(x) + cos(y); fsurf(f, [-pi pi -5 5])

Постройте параметрированную поверхность
для и .
Улучшите внешний вид графика при помощи camlight.
syms s t r = 2 + sin(7*s + 5*t); x = r*cos(s)*sin(t); y = r*sin(s)*sin(t); z = r*cos(t); fsurf(x, y, z, [0 2*pi 0 pi]) camlight view(46,52)

Постройте кусочное выражение бутылки Клейна
для и .
Покажите, что бутылка Клейна имеет только одностороннюю поверхность.
syms u v; r = @(u) 4 - 2*cos(u); x = piecewise(u <= pi, -4*cos(u)*(1+sin(u)) - r(u)*cos(u)*cos(v),... u > pi, -4*cos(u)*(1+sin(u)) + r(u)*cos(v)); y = r(u)*sin(v); z = piecewise(u <= pi, -14*sin(u) - r(u)*sin(u)*cos(v),... u > pi, -14*sin(u)); h = fsurf(x,y,z, [0 2*pi 0 2*pi]);

Для и от к , постройте 3-D поверхность . Добавьте заголовок и подписи по осям.
Создайте метки деления оси X путем охвата пределов оси X с промежутками в pi/2. Преобразуйте пределы по осям точным множителям pi/2 при помощи round и получите символьные значения деления в S. Отобразите эти метки деления при помощи XTick свойство. Создайте метки оси X при помощи arrayfun применять texlabel к S. Отобразите эти метки при помощи XTickLabel свойство. Повторите эти шаги для оси Y.
Чтобы использовать LaTeX в графиках, смотрите latex.
syms x y fsurf(y.*sin(x)-x.*cos(y), [-2*pi 2*pi]) title('ysin(x) - xcos(y) for x and y in [-2\pi,2\pi]') xlabel('x') ylabel('y') zlabel('z') ax = gca; S = sym(ax.XLim(1):pi/2:ax.XLim(2)); S = sym(round(vpa(S/pi*2))*pi/2); ax.XTick = double(S); ax.XTickLabel = arrayfun(@texlabel,S,'UniformOutput',false); S = sym(ax.YLim(1):pi/2:ax.YLim(2)); S = sym(round(vpa(S/pi*2))*pi/2); ax.YTick = double(S); ax.YTickLabel = arrayfun(@texlabel,S,'UniformOutput',false);

Постройте параметрическую поверхность , , с различными стилями линии для различных значений для , используйте пунктирную линию с зелеными точечными маркерами. Для , используйте LineWidth из 1 и зеленый цвет поверхности. Для , выключите линии установкой EdgeColor к none.
syms s t fsurf(s*sin(t),-s*cos(t),t,[-5 5 -5 -2],'--.','MarkerEdgeColor','g') hold on fsurf(s*sin(t),-s*cos(t),t,[-5 5 -2 2],'LineWidth',1,'FaceColor','g') fsurf(s*sin(t),-s*cos(t),t,[-5 5 2 5],'EdgeColor','none')

Постройте параметрическую поверхность
Задайте выход, чтобы сделать fcontour возвратите объект графика.
syms u v x = exp(-abs(u)/10).*sin(5*abs(v)); y = exp(-abs(u)/10).*cos(5*abs(v)); z = u; fs = fsurf(x,y,z)

fs =
ParameterizedFunctionSurface with properties:
XFunction: [1x1 sym]
YFunction: [1x1 sym]
ZFunction: [1x1 sym]
EdgeColor: [0 0 0]
LineStyle: '-'
FaceColor: 'interp'
Show all properties
Измените область значений u к [-30 30] при помощи URange свойство fs. Установите цвет линии на синий при помощи EdgeColor свойство и задает белые, точечные маркеры при помощи Marker и MarkerEdgeColor свойства.
fs.URange = [-30 30]; fs.EdgeColor = 'b'; fs.Marker = '.'; fs.MarkerEdgeColor = 'w';

Постройте несколько поверхностей с помощью векторного входа для fsurf. В качестве альтернативы используйте hold on построить последовательно на той же фигуре. При отображении нескольких поверхностей на той же фигуре прозрачность полезна. Настройте прозрачность объемных поверхностных диаграмм при помощи FaceAlpha свойство. FaceAlpha варьируется от 0 к 1, где 0 полная прозрачность и 1 не прозрачность.
Постройте плоскости и использование векторного входа к fsurf. Покажите обе плоскости путем создания их половиной прозрачного использования FaceAlpha.
syms x y h = fsurf([x+y x-y]); h(1).FaceAlpha = 0.5; h(2).FaceAlpha = 0.5; title('Planes (x+y) and (x-y) at half transparency')

Управляйте разрешением объемной поверхностной диаграммы с помощью 'MeshDensity' опция. Увеличение 'MeshDensity' может сделать более сглаженные, более точные графики, в то время как уменьшение его может увеличить скорость графического вывода.
Разделите фигуру на два использования subplot. В первом подграфике постройте параметрическую поверхность , , и . Поверхность имеет большой разрыв. Устраните эту проблему путем увеличения 'MeshDensity' к 40 во втором подграфике. fsurf заполняет разрыв, показывающий это путем увеличения 'MeshDensity' вы увеличили разрешение графика.
syms s t subplot(2,1,1) fsurf(sin(s), cos(s), t/10.*sin(1./s)) view(-172,25) title('Default MeshDensity = 35') subplot(2,1,2) fsurf(sin(s), cos(s), t/10.*sin(1./s),'MeshDensity',40) view(-172,25) title('Increased MeshDensity = 40')

Покажите контуры для объемной поверхностной диаграммы выражения f путем установки 'ShowContours' опция к 'on'.
syms x y f = 3*(1-x)^2*exp(-(x^2)-(y+1)^2)... - 10*(x/5 - x^3 - y^5)*exp(-x^2-y^2)... - 1/3*exp(-(x+1)^2 - y^2); fsurf(f,[-3 3],'ShowContours','on')

Создайте анимации путем изменения отображенного выражения с помощью FunctionXFunction YFunction , и ZFunction свойства и затем при помощи drawnow обновить график. Чтобы экспортировать в GIF, смотрите imwrite.
Путем варьирования переменной i от 1 до 3, анимируйте параметрическую поверхность
для-0.1 < u < 0.1 и 0 < v < 1. Увеличьте скорость графического вывода путем сокращения MeshDensity к 9.
syms s t h = fsurf(t.*sin(s), cos(s), sin(1./s), [-0.1 0.1 0 1]); h.MeshDensity = 9; for i=1:0.05:3 h.ZFunction = sin(i./s); drawnow end
Создайте символьное выражение f для функции
Постройте выражение f как поверхность. Улучшите внешний вид объемной поверхностной диаграммы при помощи свойств указателя, возвращенного fsurf, свойства подсветки и colormap.
Создайте свет при помощи camlight. Увеличьте яркость при помощи brighten. Удалите линии установкой EdgeColor к 'none'. Увеличьте рассеянный свет с помощью AmbientStrength. Для получения дополнительной информации см. Освещение, прозрачность и затенение (MATLAB). Включите поле осей. Для заголовка преобразуйте f к LaTeX с помощью latex. Наконец, чтобы улучшить внешний вид меток деления осей, метки осей и заголовок, устанавливают 'Interpreter' к 'latex'.
syms x y f = 3*(1-x)^2*exp(-(x^2)-(y+1)^2)... - 10*(x/5 - x^3 - y^5)*exp(-x^2-y^2)... - 1/3*exp(-(x+1)^2 - y^2); h = fsurf(f,[-3 3]); camlight(110,70) brighten(0.6) h.EdgeColor = 'none'; h.AmbientStrength = 0.4; a = gca; a.TickLabelInterpreter = 'latex'; a.Box = 'on'; a.BoxStyle = 'full'; xlabel('$x$','Interpreter','latex') ylabel('$y$','Interpreter','latex') zlabel('$z$','Interpreter','latex') title_latex = ['$' latex(f) '$']; title(title_latex,'Interpreter','latex')

Постройте цилиндрический интерпретатор, ограниченный ниже плоскость и выше плоскостью .
syms r t u fsurf(cos(t),sin(t),u*(cos(t)+2),[0 2*pi 0 1]) hold on;
Добавьте объемную поверхностную диаграмму плоскости .
fsurf(r*cos(t),r*sin(t),r*cos(t)+2,[0 1 0 2*pi])

Примените вращение и перевод в объемную поверхностную диаграмму торуса.
Торус может быть задан параметрически
где
угол в полярных координатах и азимутальный угол
радиус трубы
расстояние от центра трубы к центру торуса
Задайте значения для и как 1 и 5, соответственно. Постройте торус с помощью fsurf.
syms theta phi a = 1; R = 4; x = (R + a*cos(theta))*cos(phi); y = (R + a*cos(theta))*sin(phi); z = a*sin(theta); fsurf(x,y,z,[0 2*pi 0 2*pi]) hold on
Примените вращение к торусу вокруг ось. Задайте матрицу вращения. Вращайте торус 90 градусами или радианы.
alpha = pi/2;
Rx = [1 0 0;
0 cos(alpha) -sin(alpha);
0 sin(alpha) cos(alpha)];
r = [x; y; z];
r_90 = Rx*r;Переключите центр торуса 5 вперед ось. Добавьте второй график вращаемого и переведенного торуса к существующему графику.
fsurf(r_90(1)+5,r_90(2),r_90(3))
axis([-5 10 -5 10 -5 5])
hold off
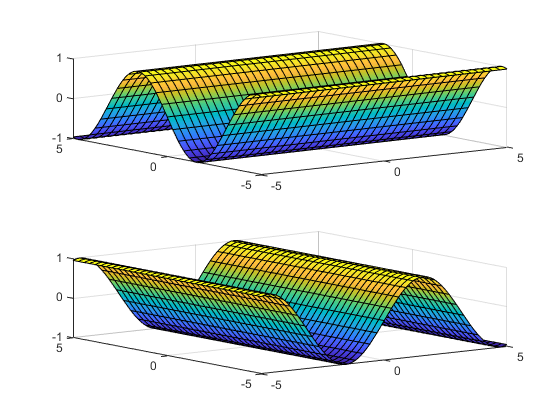
fsurf присваивает символьные переменные в f к x ось, затем y ось и symvar определяет порядок переменных, которые будут присвоены. Поэтому переменная и имена оси не могут соответствовать. Обеспечивать fsurf чтобы присвоить x или y к его соответствующей оси, создайте символьную функцию, чтобы построить, затем передать символьную функцию fsurf.
Например, следующий код строит f (x, y) = sin (y) двумя способами. Первый путь обеспечивает волны, чтобы колебаться относительно оси y. Второй путь присваивает y оси x, потому что это является первым (и только) переменная в символьной функции.
syms x y; f(x,y) = sin(y); figure; subplot(2,1,1) fsurf(f); subplot(2,1,2) fsurf(f(x,y)); % Or fsurf(sin(y));