Решите дифференциальные уравнения Используя преобразование Лапласа

Решите дифференциальные уравнения при помощи Преобразований Лапласа в Symbolic Math Toolbox™ с этим рабочим процессом. Для простых примеров на Преобразовании Лапласа смотрите laplace и ilaplace.

Определение: преобразование Лапласа

Преобразование Лапласа функционального f (t)

$F (s) = \int_{0}^{\infty} f (t) e^{- t s} d t .$

Концепция: Используя символьные рабочие процессы

Символьные рабочие процессы сохраняют вычисления в естественной символьной форме вместо числовой формы. Этот подход помогает вам изучить свойства своего решения и использовать точные символьные значения. Вы заменяете числами вместо символьных переменных только, когда вы требуете числового результата, или вы не можете продолжить символически. Для получения дополнительной информации смотрите, Выбирают Numeric or Symbolic Arithmetic. Как правило, шаги:

Объявите уравнения.
Решите уравнения.
Замените значениями.
Постройте результаты.
Анализ результатов.

Рабочий процесс: решите схему RLC Используя преобразование Лапласа

Объявите уравнения

Можно использовать Преобразование Лапласа, чтобы решить дифференциальные уравнения с начальными условиями. Например, можно решить конденсатор индуктора сопротивления (RLC) схемы, такие как эта схема.

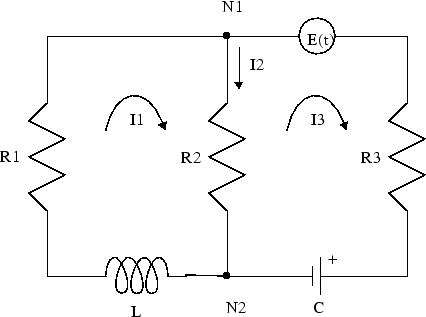
Сопротивления в Оме: _R1, _R2, _R3
Токи в ампере: _I1, _I2, _I3
Индуктивность в henry: L
Емкость в фараде: C
Электродвижущая сила в вольтах: E (t)
Заряд в кулоне: Q (t)

Примените напряжение Кирхгоффа и действующие законы, чтобы получить дифференциальные уравнения для схемы RLC.

$\frac{d I_{1}}{d t} + \frac{R_{2}}{L} \frac{d Q}{d t} = \frac{R_{2} - R_{1}}{L} I_{1} .$

$\frac{d Q}{d t} = \frac{1}{R_{3} + R_{2}} (E (t) - \frac{1}{C} Q (t)) + \frac{R_{2}}{R_{3} + R_{2}} I_{1} .$

Объявите переменные. Поскольку физические количества имеют положительные значения, устанавливают соответствующие предположения на переменных. Позвольте E (t) быть переменным напряжением 1 В.

syms L C I1(t) Q(t) s
R = sym('R%d',[1 3]);
assume([t L C R] > 0)
E(t) = 1*sin(t);        % Voltage = 1 V

Объявите дифференциальные уравнения.

dI1 = diff(I1,t);
dQ = diff(Q,t);
eqn1 = dI1 + (R(2)/L)*dQ == (R(2)-R(1))/L*I1
eqn2 = dQ == (1/(R(2)+R(3))*(E-Q/C)) + R(2)/(R(2)+R(3))*I1

eqn1(t) =
diff(I1(t), t) + (R2*diff(Q(t), t))/L == -(I1(t)*(R1 - R2))/L
eqn2(t) =
diff(Q(t), t) == (sin(t) - Q(t)/C)/(R2 + R3) + (R2*I1(t))/(R2 + R3)

Примите, что начальным током и зарядом, _I0 и _Q0, является оба 0. Объявите эти начальные условия.

cond1 = I1(0) == 0
cond2 = Q(0) == 0

cond1 =
I1(0) == 0
cond2 =
Q(0) == 0

Решите уравнения

Вычислите Преобразование Лапласа eqn1 и eqn2.

eqn1LT = laplace(eqn1,t,s)
eqn2LT = laplace(eqn2,t,s)

eqn1LT =
s*laplace(I1(t), t, s) - I1(0) - (R2*(Q(0) - s*laplace(Q(t), t, s)))/L == ...
-((R1 - R2)*laplace(I1(t), t, s))/L
eqn2LT =
s*laplace(Q(t), t, s) - Q(0) == (R2*laplace(I1(t), t, s))/(R2 + R3) + ...
(C/(s^2 + 1) - laplace(Q(t), t, s))/(C*(R2 + R3))

Функциональный solve решает только для символьных переменных. Поэтому использовать solve, сначала замените laplace(I1(t),t,s) и laplace(Q(t),t,s) с переменными I1_LT и Q_LT.

syms I1_LT Q_LT
eqn1LT = subs(eqn1LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn1LT =
I1_LT*s - I1(0) - (R2*(Q(0) - Q_LT*s))/L == -(I1_LT*(R1 - R2))/L

eqn2LT = subs(eqn2LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn2LT =
Q_LT*s - Q(0) == (I1_LT*R2)/(R2 + R3) - (Q_LT - C/(s^2 + 1))/(C*(R2 + R3))

Решите уравнения для I1_LT и Q_LT.

eqns = [eqn1LT eqn2LT];
vars = [I1_LT Q_LT];
[I1_LT, Q_LT] = solve(eqns,vars)

I1_LT =
(R2*Q(0) + L*I1(0) - C*R2*s + L*s^2*I1(0) + R2*s^2*Q(0) + C*L*R2*s^3*I1(0) + ...
C*L*R3*s^3*I1(0) + C*L*R2*s*I1(0) + C*L*R3*s*I1(0))/((s^2 + 1)*(R1 - R2 + L*s + ...
C*L*R2*s^2 + C*L*R3*s^2 + C*R1*R2*s + C*R1*R3*s - C*R2*R3*s))
Q_LT =
(C*(R1 - R2 + L*s + L*R2*I1(0) + R1*R2*Q(0) + R1*R3*Q(0) - R2*R3*Q(0) + ...
L*R2*s^2*I1(0) + L*R2*s^3*Q(0) + L*R3*s^3*Q(0) + R1*R2*s^2*Q(0) + R1*R3*s^2*Q(0) - ...
R2*R3*s^2*Q(0) + L*R2*s*Q(0) + ...
L*R3*s*Q(0)))/((s^2 + 1)*(R1 - R2 + L*s + C*L*R2*s^2 + C*L*R3*s^2 + ...
                C*R1*R2*s + C*R1*R3*s - C*R2*R3*s))

Вычислите _I1 и Q путем вычисления обратного Преобразования Лапласа I1_LT и Q_LT. Упростите результат. Подавите выход, потому что это длинно.

I1sol = ilaplace(I1_LT,s,t);
Qsol = ilaplace(Q_LT,s,t);
I1sol = simplify(I1sol);
Qsol = simplify(Qsol);

Замените значениями

Прежде, чем построить результат, замените символьными переменными числовыми значениями элементов схемы. Позвольте R 1 = 4 Ω , R2 = 2 Ω, R3 = 3 Ω, C = 1/4 F, L = 1.6 H, _I1 (0) = 15 А и Q (0) = 2 C.

vars = [R L C I1(0) Q(0)];
values = [4 2 3 1.6 1/4 15 2];
I1sol = subs(I1sol,vars,values)
Qsol = subs(Qsol,vars,values)

I1sol =
15*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) - ...
        (293*1001^(1/2)*sinh((1001^(1/2)*t)/40))/21879) - (5*sin(t))/51
Qsol =
(4*sin(t))/51 - (5*cos(t))/51 + (107*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) + ...
        (2039*1001^(1/2)*sinh((1001^(1/2)*t)/40))/15301))/51

Постройте результаты

Постройте текущий I1sol и заряжайте Qsol. Покажите и поведение переходного и устойчивого состояния при помощи двух различных временных интервалов: 0 ≤ t ≤ 10 и 5 ≤ t ≤ 25.

subplot(2,2,1)
fplot(I1sol,[0 10])                      
title('Current')
ylabel('I1(t)')
xlabel('t')

subplot(2,2,2)
fplot(Qsol,[0 10])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')

subplot(2,2,3)
fplot(I1sol,[5 25])                  
title('Current')
ylabel('I1(t)')
xlabel('t')
text(7,0.25,'Transient')
text(16,0.125,'Steady State')

subplot(2,2,4)
fplot(Qsol,[5 25])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')
text(7,0.25,'Transient')
text(15,0.16,'Steady State')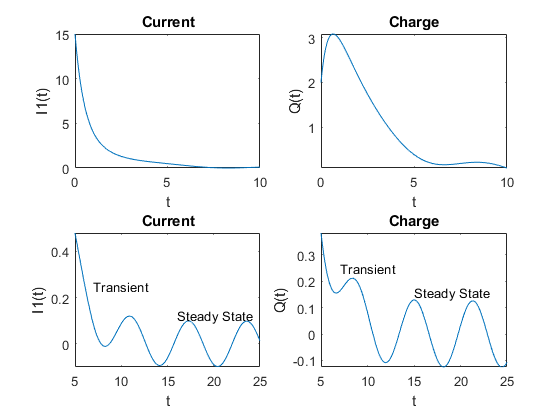

Анализ результатов

Первоначально, текущее уменьшение и уменьшение заряда экспоненциально. Однако за длительный срок, они являются колебательными. Эти поведения называются "переходным" и "устойчивым состоянием", соответственно. Символьным результатом можно анализировать свойства результата, который не возможен числовыми результатами.

Визуально смотрите I1sol и Qsol. Они - сумма условий. Найдите условия при помощи children. Затем найдите вклады условий путем графического вывода их по [0 15]. Графики показывают условия переходного и устойчивого состояния.

I1terms = children(I1sol);
Qterms = children(Qsol);

subplot(1,2,1)
fplot(I1terms,[0 15])
ylim([-2 2])
title('Current terms')

subplot(1,2,2)
fplot(Qterms,[0 15])
ylim([-2 2])
title('Charge terms')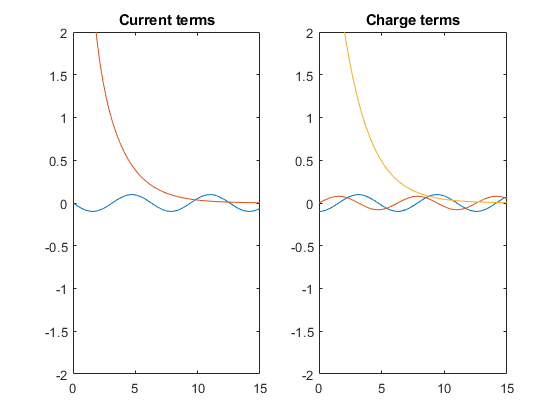

Графики показывают тот I1sol имеет термин переходного и устойчивого состояния, в то время как Qsol имеет переходный процесс и два условия устойчивого состояния. От визуального осмотра заметьте I1sol и Qsol имейте термин, содержащий exp функция. Примите, что этот термин вызывает переходное экспоненциальное затухание. Разделите условия переходного и устойчивого состояния в I1sol и Qsol путем проверки условий на exp использование has.

I1transient = I1terms(has(I1terms,'exp'))
I1steadystate = I1terms(~has(I1terms,'exp'))

I1transient =
15*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) - (293*1001^(1/2)*sinh((1001^(1/2)*t)/40))/21879)
I1steadystate =
-(5*sin(t))/51

Точно так же отдельный Qsol в условия переходного и устойчивого состояния. Этот результат демонстрирует, как символьные вычисления помогают вам анализировать свою проблему.

Qtransient = Qterms(has(Qterms,'exp'))
Qsteadystate = Qterms(~has(Qterms,'exp'))

Qtransient =
(107*exp(-(51*t)/40)*(cosh((1001^(1/2)*t)/40) + (2039*1001^(1/2)*sinh((1001^(1/2)*t)/40))/15301))/51
Qsteadystate =
[ -(5*cos(t))/51, (4*sin(t))/51]

Документация