Обработайте выражения, вовлекающие функции Хивизида и Дирак

Вычислите производные и интегралы выражений, включающих дельту Дирака и функции Heaviside.

Найдите первые и вторые производные функции Heaviside. Результатом является функция дельты Дирака и ее первая производная.

syms x
diff(heaviside(x), x)
diff(heaviside(x), x, x)

ans =
dirac(x)
 
ans =
dirac(1, x)

Найдите неопределенный интеграл функции дельты Дирака. Результаты возвращены int не включайте константы интегрирования.

int(dirac(x), x)

ans =
sign(x)/2

Найдите интеграл синусоидальной функции, включающей функцию дельты Дирака.

syms a
int(dirac(x - a)*sin(x), x, -Inf, Inf)

ans =
sin(a)

Используйте предположения на переменных

dirac учитывает предположения на переменных.

syms x real
assumeAlso(x ~= 0)
dirac(x)

ans =
0

Для дальнейших расчетов очистите предположения на x путем воссоздания его с помощью syms.

syms x

Оцените Дирака функция Delta для символьной матрицы

Вычислите функцию дельты Дирака x и его первые три производные.

Используйте векторный n = [0,1,2,3] задавать порядок производных. dirac функция расширяет скаляр в вектор одного размера с n и вычисляет результат.

syms x
n = [0,1,2,3];
d = dirac(n,x)

d =
[ dirac(x), dirac(1, x), dirac(2, x), dirac(3, x)]

Замените x с 0.

subs(d,x,0)

ans =
[ Inf, -Inf, Inf, -Inf]

Постройте Дирака функция Delta

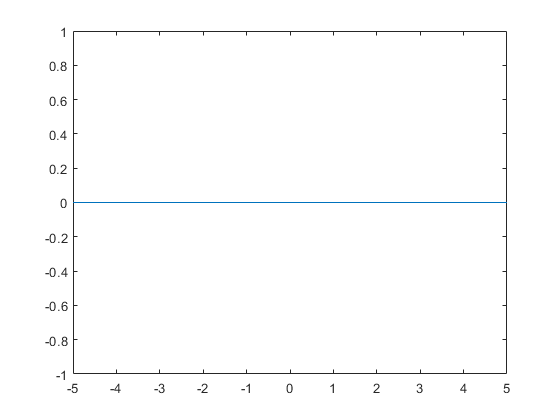
Можно использовать fplot чтобы построить дельту Дирака функционируют на интервале по умолчанию [-5 5]. Однако dirac(x) возвращает Inf в x равняйтесь 0, и fplot не строит бесконечность.

Объявите символьную переменную x и постройте символьное выражение dirac(x) при помощи fplot.

syms x
fplot(dirac(x))

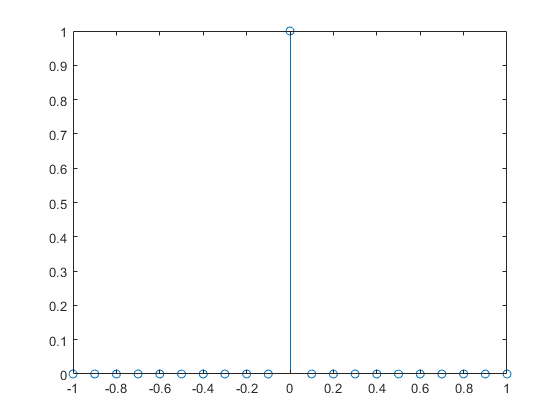
Обрабатывать бесконечность в x равняйтесь 0, используйте числовые значения вместо символьных значений. Установите Inf значение к 1 и постройте функцию дельты Дирака при помощи stem.

x = -1:0.1:1;
y = dirac(x);
idx = y == Inf; % find Inf
y(idx) = 1;     % set Inf to finite value
stem(x,y)